Вопрос 25: формула Тейлора с остаточным членом в форме Лагранжа

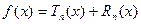Формула Тейлора представляет собой один из основных инструментов математического анализа. Её смысл состоит в том, что функция представляется в виде , где – многочлен Тейлора, – остаточный член формулы Тейлора. В зависимости от вида она используется в различных целях: при вычислениях значений функций с заданной точностью, при исследовании асимптотического поведения функций и т.д.

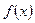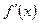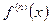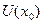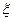Теорема 25.1 (формула Тейлора с остаточным членом в форме Лагранжа) Пусть , , …, непрерывны в окрестности точки и пусть в существует . Тогда для любого существует точка , лежащая между и 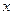такая, что

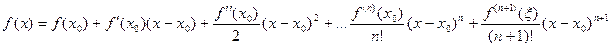(1)

Примечание. В этом представлении функции величина называется остаточным членом в форме Лагранжа.

Можно выписать более общую форму Шлёмильха и Роша (Schlömilch–Roche) остаточного члена:

, (2)

где – число, удовлетворяющее неравенствам 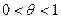, такое, что 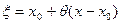, а 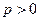– любое число. Например, остаточный член в форме Лагранжа получится, если 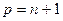в этой общей форме (2). Иногда бывает удобен остаточный член в форме Коши, получаемый из (2) при :

.

Однако наиболее часто используется остаточный член в форме Лагранжа и мы докажем формулу Тейлора именно в таком виде.

◄Рассмотрим вспомогательную функцию

(3)

Поскольку эта функция 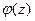получится вычитанием из 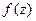многочлена от , а многочлен непрерывен и имеет непрерывные производные любого порядка, для функции 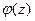сохраняются свойства функции 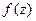, т.е. 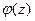, , …, непрерывны в 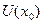и существует в .

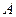Пусть . Для определённости, пусть . Выберем число так, чтобы выполнялось равенство 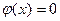. Это возможно, поскольку при подстановке 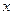вместо в (3), это равенство примет вид линейного относительно уравнения с коэффициентом при 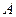, равным .

Теперь для применения следствия теоремы 23.2(Ролля) осталось только доказать, что выполняются равенства .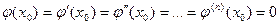

Для этого сначала вычислим 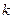-ю производную, , от функции 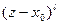в точке .

По формуле для производной степенной функции последовательно получаем:

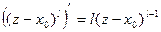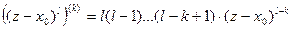, , …, , если . В точке эта величина обращается в 0.

Если 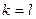, то .

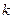Если же , то дальнейшее дифференцирование даст тождественный ноль. (Степень многочлена равна , т.е. он имеет вид , -кратное дифференцирование при каждого слагаемого, входящего в этот многочлен, даёт тождественный ноль)

Итак, все производные порядка 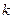, , функции равны 0 в точке , а .

Равенство 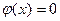справедливо по выбору 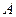. Для любого 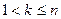имеем, согласно доказанному выше

Все условия следствия теоремы 23.2 (Ролля) выполнены, поэтому существует точка 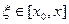, такая, что . Но , значит ,т.е.

(4)

Вспоминаем, что 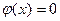и подставляем 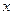вместо в формулу (3), учитывая (4):
, что означает:

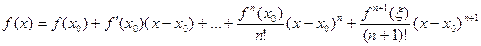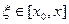, (5)

Случай, когда 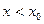вполне аналогичен и приводит к такому же равенству (5). ◄

Замечание 1. Часто вместо 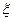пишут 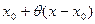, где 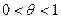и наоборот, каждому такому 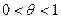соответствует число 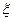между и .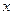

Замечание 2. Часто вместо точки пишут просто 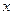, а вместо 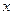пишут 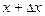и формула Тейлора приобретает вид:

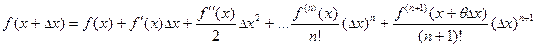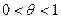, (6)

Замечание 3. В случае, когда 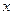– независимая переменная, или линейная функция от независимой переменной, , и . Обозначим . При этом формула Тейлора записывается так:

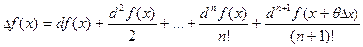(7)

Замечание 4. Особенно часто формула Тейлора используется, когда . Тогда и

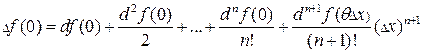(8)

Эту формулу часто называют также формулой Маклорена (Mac-Laurin).

Дата добавления: 2015-04-24