Уйгели В.В., Пратусевич А.Е., Корнаев А.В., Доронин О.Н. 1 страница

А

А

Из рисунка видно, что А = В È (А \ В), откуда n (А) = n (В È (А \ В)). Поскольку В Ç (А\В) = Æ, то получим n (А) = n (В) + n (А \ В) или а = в + (а – в). Данное равенство показывает, что разность а - в есть такое число, сумма которого и числа в равна числу а.

Данный факт позволяет по-другому дать определение значения разности.

Значением разности натуральных чисел а и в называется такое натуральное число с, сумма которого и числа в равна а.

Аналогично можно провести теоретико-множественное истолкование обратной связи. Таким образом, а - в = с Û а = в + с.

Говорят, что действие вычитания является обратным действию сложения.

В курсе математики периода детства первоначально вычитание натуральных чисел рассматривается на основе практических упражнений, связанных с выделением подмножества данного множества и образованием нового множества – дополнения выделенного подмножества. При этом главным средством раскрытия теоретико-множественного смысла вычитания является решение простых текстовых задач.

Рассмотрим свойства, связанные с действием вычитания.

1. Разность натуральных чисел а и в существует и единственна тогда и только тогда, когда в < а.

2. Правило вычитания числа из суммы: (а + в) – с = (а – с)+ в = а + (в – с), если а > c и в > c.

3. Правило вычитания суммы из числа: а – (в +с) = (а – в) – с = (а – с) – в.

4. Правило вычитания разности из числа: а – (в - с) = (а – в) + с = (а + с) – в.

5. Правило прибавления разности к числу: а +(в - с) =(а + в) – с = (а – с) + в, если а > c.

Дадим теоретико-множественное обоснование правила вычитания суммы из числа. С этой целью рассмотрим три конечных множества А, В и С таких, чтоn (А) = а, n (В) = в, n (С) = с, В ÇС = Æ и В È С Ì А. Тогда а – (в + с) = n (А\ (В È С)), (а – в) – с = n ((А\ В) \ С), (а – с) – в = n ((А\ С) \ В).

Покажем сначала, что выполняется равенство а – (в +с) = (а – в) – с.

Рис. (а) Рис. (б)

На диаграммах Эйлера-Венна множество А\ (В È С) представлено светлой областью на рисунке (а), а множество (А\ В) \ С – темной областью на рисунке (б). Сравнивая указанные области, убеждаемся в том, что они одинаковы. Значит, для множеств А, В и С выполняется равенство А\ (В È С) = (А\ В) \ С. Следовательно, n(А\(В È С)) = n((А\ В)\ С), то есть а – (в +с) = (а – в) – с.

Аналогично показывается, что а – (в +с) = (а – с) – в. И, на основании этого, делается вывод о выполнимости свойства вычитания из числа суммы а – (в +с) = (а – в) – с = (а – с) – в.

Понятие произведения натуральных чисел в количественной теории может быть определено по-разному. Рассмотрим сначала подход, в основе которого лежит понятие суммы.

Произведением натуральных чисел а и в называется такое натуральное число а × в, которое удовлетворяет следующим условиям:

1) а × в = а + а +…..+ а при в > 1;

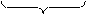
в слагаемых

2) а × 1 = а при в = 1;

3) а × 0 = 0 при в = 0.

Действие, при помощи которого находят значение произведения чисел а и в, называется умножением, числа а и в называются множителями, выражение а × в – произведением, число, полученное в результате умножения, называется значением произведения.

Данное определение произведения имеет следующий теоретико-множественный смысл. Если множества А₁, А₂, А₃, …, А _в имеют по а элементов каждое и никакие два из них не пересекаются, то их объединение содержит а × в элементов. Следовательно, произведение а × в – это число элементов в объединении в попарно непересекающихся множеств, каждое из которых содержит по а элементов.

С данным подходом к умножению учащиеся знакомятся в начальных классах. В учебнике математики дается следующее определение умножения: «Сложение одинаковых слагаемых называется умножением». Смысл этого определения раскрывается при решении простых задач.

Например, рассмотрим задачу: «На каждую рубашку нужно пришить 5 пуговиц. Сколько пуговиц нужно пришить на 4 таких рубашки?». В данной задаче требуется найти число элементов в объединении, состоящем из 4 множеств, а в каждом множестве содержится по 5 элементов. Согласно определению это число находится умножением: 5 × 4=20 (пуговиц).

Второй подход к определению действия умножения связан с декартовым произведением двух множеств. Пусть нам даны два множества А = {а, в, с} и В = {1, 2}. Найдем их декартово произведение, которое запишем в виде прямоугольной таблицы:

(а, 1), (в, 1), (с, 1),

(а, 2), (в, 2), (с, 2).

В каждой строке таблицы все пары имеют одинаковую вторую компоненту, а в каждом столбце одинаковая первая компонента. При этом строки не имеют ни одной одинаковой пары. Отсюда следует, что число элементов в декартовом произведении данных множеств А х В равно 3 + 3 = 6. С другой стороны, n (А) = 3, n (В) = 2 и 3 × 2 = 6. Видим, что число элементов в декартовом произведении данных множеств А и В равно произведению n (А) × n (В).

Вообще, если А и В – конечные множества, то n (А х В) = n (А) × n (В).

Таким образом, произведением натуральных чисел а и в называется натуральное число а × в, равное числу элементов декартова произведения множеств А и В таких, что n (А) = а, n (В) = в.

Рассмотрим основные законы, которым удовлетворяет операция умножения натуральных чисел.

1. Каковы бы ни были два натуральных числа а и в, всегда существует единственное натуральное число с, являющееся их значением произведения. Другими словами, значение произведения любых двух натуральных чисел всегда существует и есть число единственное.

2. Коммутативный закон умножения: (" а, в Î N) (а × в = в × а).

3. Ассоциативный закон умножения: (" а, в, с Î N) ((а × в) × с = а × (в × с)).

4. Монотонность умножения: (" а, в, с Î N) (если а < в, то а × с < в × с).

5. Дистрибутивность умножения относительно сложения слева: (" а, в, с Î N) (а× (в +с) = а × в + а × с).

6. Дистрибутивность умножения относительно сложения справа: (" а, в, с Î N) ((а + в)× с = а × с + в × с).

7. Дистрибутивность умножения относительно вычитания слева: (" а, в, с Î N) (а× (в - с) = а × в - а × с).

8. Дистрибутивность умножения относительно вычитания справа: (" а, в, с Î N) ((а - в)× с = а × с - в × с).

Справедливость данных законов опирается на выполнимость соответствующих свойств для операций над множествами.

Докажем справедливость закона 5. Для того возьмем конечные множества А, В и С, которые удовлетворяют следующим условиям: n (А) = а, n (В) = в, n (С) = с и В Ç С = Æ.

Поскольку для любых множеств имеет место дистрибутивность декартова произведения относительно объединения, то он выполняется и для наших множеств А, В и С, то есть А х (В È С) = (А х В) È (А х С).

Из равенства конечных множеств вытекает равенство их численностей. Это означает, что n (А х (В È С)) = n ((А х В) È (А х С)). Но n (А х (В È С)) = а× (в +с), а n ((А х В) È (А х С))= а× в + а × с, что и требовалось доказать.

Рассмотрим теоретико-множественный смысл частного. Операция деления на множестве натуральных чисел связана с разбиением множества на классы. При этом решаются две задачи.

1. 10 яблок разложили на несколько тарелок, по 2 яблока на каждую тарелку. Сколько тарелок потребовалось?

Ответ на вопрос задачи находится действием деления:

10: 2 = 5 (тарелок).

Проанализируем решение этой задачи. В задаче рассматривается множество, в котором 10 элементов. Оно разбивается на подмножества, в каждом из которых по 2 элемента, т.е. на равночисленные подмножества. Кроме того, они попарно не пересекаются. В задаче спрашивается, сколько таких подмножеств получилось. Таким образом, число 5, полученное в ответе, - это число двухэлементных подмножеств, на которое разбито множество из 10 элементов.

2. Учительница раздала 6 тетрадей 3 ученикам поровну. Сколько тетрадей получил каждый ученик?

Данная задача также решается действием делением:

6: 3 = 2 (тетради).

Но число 2 здесь играет другую роль – оно обозначает число элементов в каждом из трех равночисленных непересекающихся подмножеств, на которые разбито множество, состоящее из 6 элементов.

Опишем эти задачи в общем виде и дадим определение частного натуральных чисел.

1. Имеем множество А, такое что n (А) = а. Данное множество необходимо разбить на попарно непересекающиеся подмножества, в каждом из которых содержится по в элементов. Тогда частное а: в показывает, сколько подмножеств содержится в таком разбиении. В этом случае говорят о делении по содержанию.

2. Имеем множество А, такое что n (А) = а. Теперь множество необходимо разбить на в равночисленных попарно непересекающихся подмножеств. Тогда частное а: в показывает, сколько элементов содержится в каждом подмножестве. В этом случае говорят о делении на равные части.

Таким образом, определение частного натуральных чисел будет иметь следующий вид:

Пусть а = n (А) и множество А разбито на равночисленные попарно непересекающиеся подмножества, тогда

1) если в – число элементов каждого подмножества, то частным а: в называется число подмножеств в разбиении;

2) если в – число подмножеств в разбиении, то частным а: в называется число элементов каждого подмножества.

В записи а: в = с число а называется делимым, число в –делителем, выражение а: в – частным, а число с - значением частного. Действие, при помощи которого находят значение частного, называется делением.

В математике, чтобы проверить правильность выполнения действия деления обращаются к действию умножения. Это связано с тем, что между действиями умножения и деления имеется определенная связь. Покажем что это за связь.

Пусть а = n(А) и множество А разбито на в попарно непересекающихся равночисленных подмножеств, т.е. А = А₁ È А₂ È А₃ È … È А _в, где n (А₁) = n (А₂) = n (А₃) = …= n (А _в) = а: в = с.

Но тогда по определению суммы n(А) = n (А₁ È А₂ È А₃ È … È А _в) = n (А₁) + n (А₂) + …+ n (А _в). Учитывая определение произведения, последнее равенство можно записать так:

а = с + с + с + …+ с = с× в.

в слагаемых

Равенство а = в × с выражает связь операций деления и умножения. Данный факт позволяет по-другому дать определение значения частного.

Значением частного натуральных чисел а и в называется такое натуральное число с = а: в, которое в произведении с числом в дает число а.

Аналогично можно провести теоретико-множественное истолкование обратной связи. Таким образом, а: в = с Û а = в× с.

Рассмотрим свойства, связанные с действием деления.

1. Для того чтобы существовало значение частного натуральных чисел а и в необходимо, чтобы в ≤ а. Если значение частного существует, то оно единственно.

2. Деление на нуль невозможно.

3. Правило деления суммы на число: (а + в): с = а: с + в: с.

4. Правило деления разности на число: (а - в): с = а: с - в: с.

5. Правило деления произведения на число: (а× в): с = (а: с)× в = а× (в: с), если а с и в с.

6. Правило деления числа на произведение: а: (в × с) = (а: в): с = (а: с): в.

7. Правило умножения числа на частное: а × (в: с) = (а× в): с = (а: с)× в.

Докажем справедливость свойства 3. Пусть даны множества А и В такие, что А Ç В = Æ и n(А) = а, n(В) = в. Если множества А и В можно разбить на равночисленные подмножества, состоящие из с элементов каждое, то и объединение этих множеств допускает такое же разбиение на с подмножеств. Если при этом множество А состоит из а: с подмножеств, а В – из в:с подмножеств, то А È В состоит из а: с + в: с подмножеств. Это и означает, что (а + в): с = а: с + в: с.

Порядковая теория натуральных чисел

В конце 19 века была построена порядковая теория натуральных чисел, которая обычно связывается с именем итальянского математика Джузеппе Пеано (1858-1932гг.), построившего эту теорию на аксиоматической основе.

Аксиоматический подход к построению теории состоит в следующем: 1) выделяются некоторые исходные, неопределяемые через другие понятия; все остальные понятия теории определяются через основные или ранее определенные; 2) выделяются некоторые исходные предложения, или аксиомы, истинность которых принимается без доказательства; все остальные предложения теории – теоремы – логически выводятся или доказываются с использованием введенных понятий, ранее доказанных фактов, теорем.

Аксиоматический подход применяется для построения теории, о которой уже имеются определенные, сформированные интуитивные представления. Иначе говоря, осуществляется аксиоматизация уже имеющейся «предматематической теории».

Поход к построению теории натуральных чисел, берущий начало от Пеано, представляет собой определенный способ математизации интуитивного представления о натуральном ряде чисел.

В качестве основных (неопределяемых) используются следующие понятия: множество, элемент, содержится (принадлежит). Множество натуральных чисел обозначается N, элементы множества – а, в, с …. Основным отношением выбирается отношение «непосредственно следовать за». Элемент, непосредственно следующий за элементом а, обозначается а´.

Отношение «непосредственно следовать за» удовлетворяет следующим аксиомам Пеано:

Аксиома 1. Единица непосредственно не следует ни за каким натуральным числом (т.е. единица – это «первое» натуральное число и не является «правым соседом» никакого другого натурального числа).

Аксиома 2. Для любого натурального числа существует одно и только одно непосредственно следующее за ним натуральное число (т.е. любое натуральное число имеет только одного «правого соседа»).

Аксиома 3. Любое натуральное число непосредственно следует не более чем за одним натуральным числом (т.е. единица не следует ни за каким, всякое другое натуральное число - точно за одним).

Всякое натуральное число, кроме единицы, является «правым соседом» одного и только одного натурального числа, его «левого соседа».

Аксиома 4. Если множество М есть подмножество множества натуральных чисел N, и известно, что оно содержит единицу и вместе с некоторым натуральным числом а содержит натуральное число а´, непосредственно следующее за а, то это множество М совпадает с множеством всех натуральных чисел N (т.е. М = N).

Данная аксиома, хотя по своему содержанию более сложная, чем первые три, но она также выражает достаточно простое свойство: с помощью последовательного прибавления единицы, начиная с единицы, можно получить все натуральные числа. Всякий раз, когда мы доходим до некоторого числа а, допускается возможность написания непосредственно следующего за ним числа а´.

Опираясь на введенное отношение «непосредственно следовать за» и аксиомы 1-4, характеризующие множество N, можно дать следующее определение натурального числа.

Множество N, для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам 1-4, называется множеством натуральных чисел, а его элементы – натуральными числами.

Аксиоматический подход к теории натуральных чисел при изучении математики в период детства не рассматривается, однако те свойства отношения «непосредственно следовать за», которые нашли отражение в аксиомах 1-4, являются предметом изучения в период детства и используются при решении задач. При рассмотрении чисел первого десятка выясняется, как может быть получено каждое число. При этом широко используются понятия «следует», «предшествует», прибавление и вычитание 1. Каждое новое число с самого начала выступает как продолжение ранее изученного отрезка N натурального ряда чисел. При таком подходе создаются условия для того, чтобы дети подметили некоторые общие свойства чисел натурального ряда: не только данное, рассматриваемое на этом занятии число, но и вообще любое число может быть получено прибавлением 1 к числу, которое встречается при счете перед ним, или вычитанием 1 из числа, которое идет при счете сразу после него; любое число на 1 больше, чем ему предшествующее. Таким образом, дети убеждаются в том, что за каждым числом идет следующее и притом только одно, что натуральный ряд чисел бесконечен.

Метод математической индукции

В основе всякого математического исследования лежат дедуктивный и индуктивный методы. Дедуктивный метод рассуждений - это рассуждение от общего к частному, т.е. рассуждение, исходным моментом которого является общий результат, а заключительным моментом – частный результат. Индукция применяется при переходе от частных результатов к общим, т.е. является методом, противоположным дедуктивному.

Метод математической индукции можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно.

Слово индукция по-русски означает наведение, а индуктивными называют выводы, на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему.

Например, мы каждый день наблюдаем, что Солнце восходит с востока. Поэтому можно быть уверенным, что и завтра оно появится на востоке, а не на западе. Этот вывод мы делаем, не прибегая ни к каким предположениям о причине движения Солнца по небу (более того, само это движение оказывается кажущимся, поскольку на самом деле движется земной шар). И, тем не менее, этот индуктивный вывод правильно описывает те наблюдения, которые мы проведем завтра.

Роль индуктивных выводов в экспериментальных науках очень велика. Они дают те положения, из которых потом путем дедукции делаются дальнейшие умозаключения. И хотя теоретическая механика основывается на трех законах движения Ньютона, сами эти законы явились результатом глубокого продумывания опытных данных, в частности законов Кеплера движения планет, выведенных им при обработке многолетних наблюдений датского астронома Тихо Браге. Наблюдение, индукция оказываются полезными и в дальнейшем для уточнения сделанных предположений.

В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство |AB| + |BC| ≥ |AC|.

По своему первоначальному смыслу слово «индукция» применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частных утверждений. Простейшим методом рассуждений такого рода является полная индукция. Вот пример подобного рассуждения.

Пусть требуется установить, что каждое натуральное чётное число n в пределах 4 < n < 20 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:

4 = 2 + 2 6 = 3 + 3 8 = 5 + 3 10 = 7 + 3

12 = 7 + 5 14 = 7 + 7 16 = 11 + 5 18 = 13 + 5

20 = 13 + 7

Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.

Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.

Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция).

Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин.

Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:

1 = 1 = 1²

1 + 3 = 4 = 2²

1 + 3 + 5 = 9 = 3²

1 + 3 + 5 + 7 = 16 = 4²

1 + 3 + 5 + 7 + 9 = 25 = 5²

После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод: 1 + 3 + 5 +…+ (2 n - 1) = n² , т.е. сумма n первых последовательных нечётных чисел равна n ²

Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости приведённой формулы.

Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев мы не в состоянии. Неполная же индукция часто приводит к ошибочным результатам.

Во многих случаях выход из такого рода затруднений заключается в обращении к особому методу рассуждений, называемому методом математической индукции. Он заключается в следующем.

Пусть нужно доказать справедливость некоторого утверждения для любого натурального числа n (например нужно доказать, что сумма первых n нечётных чисел равна n²). Непосредственная проверка этого утверждения для каждого значения n невозможна, поскольку множество натуральных чисел бесконечно. Чтобы доказать это утверждение, проверяют сначала его справедливость для n = 1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n = k вытекает его справедливость и при n = k + 1.

Тогда утверждение считается доказанным для всех n. В самом деле, утверждение справедливо при n = 1. Но тогда оно справедливо и для следующего числа n = 1 + 1 = 2. Из справедливости утверждения для n = 2 вытекает его справедливость для n = 2 + 1 = 3. Отсюда следует справедливость утверждения для n = 4 и т.д. Ясно, что, в конце концов, мы дойдём до любого натурального числа n. Значит, утверждение верно для любого n.

Обобщая сказанное, сформулируем следующий общий принцип.

Принцип математической индукции: Если предложение А(n), зависящее от натурального числа n, истинно для n = 1 и из того, что оно истинно для n = k (где k - любое натуральное число), следует, что оно истинно и для следующего числа n = k + 1, то предположение А(n) истинно для любого натурального числа n.

В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n > p, где p -фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом.

Если предложение А(n) истинно при n = p и если из предположения, что оно истинно при А(k) вытекает, что оно истинно при А(k +1) для любого k > p, то предложение А(n) истинно для любого n > p.

Доказательство по методу математической индукции проводиться следующим образом. Сначала доказываемое утверждение проверяется для n = 1, т.е. устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции. Затем следует часть доказательства, называемая индукционным шагом. В этой части доказывают справедливость утверждения для n = k + 1 в предположении справедливости утверждения для n = k (предположение индукции), т.е. доказывают, что истинность A(k +1) из предположения, что оно истинно при А(k).

Пример 1. Доказать, что при любом n справедливо утверждение: 1 + 3 + 5 +…+ (2 n - 1) = n ² .

Решение:

1. Имеем n = 1 = 1². Следовательно, утверждение верно при n = 1, т.е. А(1) истинно.

2. Предположим, что А(k) истинно, то есть утверждение справедливо для n = k: 1 + 3 + 5 +…+ (2 k - 1) = k ² .

3. Докажем, что утверждение справедливо и для следующего натурального числа n = k + 1, т.е. что 1 + 3 + 5 +…+ (2 k - 1) + (2 k +1) = (k + 1) ² .

В самом деле, 1+3+5+…+(2 k -1)+(2 k +1) = k ² + 2 k + 1 = (k + 1) ² .

Итак, из того, что предложение истинно для n = 1 и из предположения, что оно истинно для n = k, следует, что оно истинно и для следующего числа n = k + 1, на основании принципа математической индукции заключаем, что предположение истинно для любого натурального числа.

Пример 2. Доказать, что при любом n справедливо утверждение: 1 + х + х ² + х ³ +…+ х ⁿ = (х ⁿ⁺¹ - 1) / (х - 1)

Решение:

1. При n = 1 получаем

1 + х = (х² - 1) / (х - 1) = (х - 1) (х + 1) / (х-1) = х + 1

следовательно, при n=1 формула верна; А(1) истинно.

2. Предположим, что формула верна при n = k, т.е.

+ х + х² + х³ +…+ х^k = (х^k+1 - 1) / (х - 1).

3. Докажем, что тогда выполняется равенство

1 + х + х² + х³ +…+ х^k + x^k+1 = (x^k+2 - 1) / (х - 1).

В самом деле

1+ х + х² + x³ +…+ х^k + x^k+1 = (1 + x + x ² + x ³ +…+ x ^k ) + x ^k+1 = (x ^k+1 -1) / (x - 1) + x ^k+1 = (x ^k+2 - 1) / (x - 1).

Итак, из того, что предложение истинно для n = 1 и из предположения, что оно истинно для n = k, следует, что оно истинно и для следующего числа n = k + 1, на основании принципа математической индукции заключаем, что предположение истинно для любого натурального числа.

Пример 3. Доказать, что при любом n справедливо утверждение: 1 ² +2 ² +3 ² +…+ n ² = n (n + 1)(2 n + 1) / 6.

Решение:

1. Пусть n = 1, тогда Х ₁ =1 ² = 1(1 + 1) (2 + 1) / 6 = 1.

Дата добавления: 2015-04-25