Теоремы о дифф. ф-ях

Производные высших порядков.

Df: Пусть ф-ия 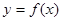дифф. на Х, то есть дифф. в каждой т. Х.

Каждому значению Х соответствует единственное значение 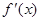, т.е. получаем 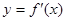как ф-ию, заданную на Х.

Если она окажется дифф. на Х, то мы можем вычислить следующую 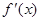, которая будет называться второй и т.д.

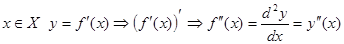
Df: Производной n - го порядка от ф-ии 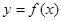называется первая производная от производной n-1 порядка.

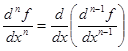
Пример:

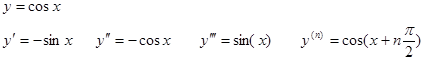
Теорема Ферма: Пусть 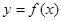дифф. на 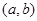и наибольшее или наименьшее ее значение в т. х₀, тогда производная в этой точке равна нулю.

**************************

Доказательство:

Пусть 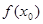- наибольшее на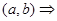

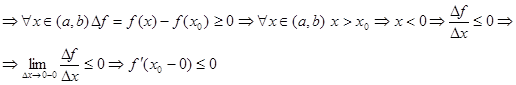
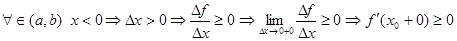
Но из дифф 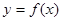в т. х₀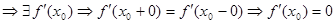

Zm: Из доказательства т. Ферма следует: Пусть 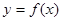непрерывна на промежутке и внутренних точках этого промежутка принимает наибольшее и наименьшее значение, тогда если в этой точке ф-ия дифф., то .

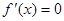Теорема Ролля: Пусть ф-ия :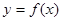

1. непрерывна на

2. дифф. на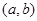

3. Принимает на концах этого отрезка одинаковые значения.

Тогда на 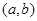существует т. х₀, в которой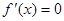

*************

Доказательство:

Из непрерывности ф-ии на отрезке следует, что имеет на этом отрезке свои наименьшее(m) и наибольшее(M) значения.

Возьмем два случая:

1. m=M; наименьшее значение совпадает с х₀ следовательно: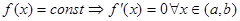

2. 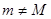; из (3) следует: ***********

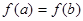Dh: Между двумя корнями ф-ии есть точка производной.

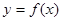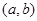Теорема Лагранжа: Пусть ф-ия непрерывна на промежутке , дифф. на , тогда на 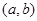существует такая х₀ такая, что верна формула:

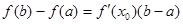
Если ее переписать в виде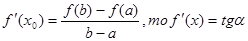

**************************

Доказательство:

Рассмотрим вспомогательную ф-ию .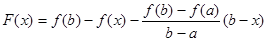

1. Она непрерывна на как сумма непрерывных ф-ий.

2. F(x) – дифф. на 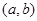как сумма дифф. на интервале ф-ий.

3. F(а) = 0; F(b) = 0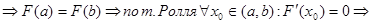

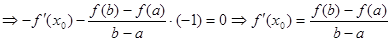
Sl: Пусть ф-ия 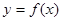дифф. на 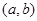, тогда для любой внутренней точки интервала справедлива формула Лагранжа:

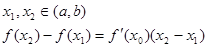х₀ между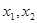

Действительно ***************

Из дифф. ф-ии на 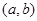следует ее непрерывность на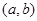

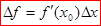
Теорема Коши: Пусть 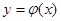и :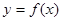

1. Непрерывны на .

2. Дифф. на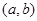

Тогда на 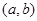существует т. х₀, для которой справедлива формула Коши:

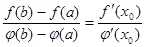
Доказывается как теорема Лагранжа.

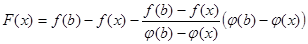
Дата добавления: 2015-03-29