Докажите, что однородная система, состоящая из трех уравнений от пяти переменных, имеет бесконечно много решений

Системы линейных уравнений

9. Какие системы уравнений называются определенными, неопределенными, несовместными? Приведите примеры. Может ли однородная система линейных уравнений быть несовместимой?

Если существует хотя бы одно решение системы – она совместна. Система, не имеющая ни одного решения, называется несовместной (появление противоречивой строки)

Например:

2*х1 + 3*х2 + х3 - 2*х4 =9

7*х1 + 8*х2 – х3 - 2*х4 =5

3*х1 + 2*х2 - 3*х3 + 2*х4 =10

Линейное уравнение называется однородным, если свободный член уравнения равен нулю. Система, состоящая из однородных уравнений, называется однородной.

Например:

Если система совместна, то она может иметь единственное решение, и в этом случае ее называют определенной.

Например: (имеет единственное решение)

х1+2*х2+3*х3=7

2*х1-х2+х3=4

3*х1-2*х2-х3=3

Систему называют неопределенной, когда она имеет бесконечно много решений (если число переменных больше, чем количества уравнений)

!!Любая однородная система совместна!!

Решим систему относительно х1,х2,х3. .

Каждый раз меняя значения, мы будем получать разные решения.

11. Докажите, что множество решений однородной системы из 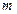уравнений с 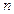неизвестными является подпространством пространства 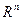. Какова размерность этого подпространства? Ответ обоснуйте.

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n = 0

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n = 0

…

a_m1x₁ + a_m2x₂ + … + a_mnx_n = 0

Решение системы х = (x₁, x₂, …, x_n). Пусть b = (b₁, b₂, …, b_n), c = (c₁, c₂, …, c_n) – являются решениями системы. Тогда b+с =(b₁+c₁, b₂+c₂, …, b_n+c_n) является решением системы (подставить в систему, раскрыть скобки). Для любого k ϵ R и b = (b₁, b₂, …, b_n) kb = (kb₁, kb₂, …, kb_n) также является решением системы. Значит, множество решений СОЛУ является подпространством Rⁿ, т. к. замкнуто относительно операций сложения и умножения вектора на число. Размерность равна m-r(рангу системы векторов).

12. Как связаны решения совместной неоднородной системы линейных уравнений 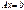и однородной системы 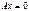? Приведите пример.

Теорема (Кронекера и Капелли): Неоднородная система уравнений Ax = b совместна тогда и только тогда, когда rangA = rangB (где B - расширенная матрица системы (B = [A|b]), получающаяся из A дописыванием свободного столбца b).

Теорема: Общее решение неоднородной системы линейных уравнений Ax = b имеет

вид x = x0 +c1x1 +...+crxr, где x0 - некоторое (частное) решение неоднородной системы,

а c1x1 +... + crxr - общее решение однородной системы Ax = 0. Пример:

A =1 1 1

1 1 −1

b=3

1, x∈ R3.

Здесь x0 = (1, 1, 1) - частное решение неоднородной системы. x1 = (1,−1, 0) - общее

уравнение однородной системы. Тогда решение x = (a, b, c) неоднородной системы:x = (a, b, c) = x0 + αx1 = (1, 1, 1) + α(1,−1, 0) = (1 + α, 1 − α, 1)

Дата добавления: 2015-03-31