Формулы численного дифференцирования интерполяционным методом

Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции.

В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).

Основными задачами являются вычисление производной на краях таблицы и в ее середине. Для равномерной сетки формулы численного дифференцирования «в начале таблицы» можно представить в общем виде следующим образом:

где — погрешность формулы. Здесь коэффициенты и 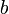зависят от степени n использовавшегося интерполяционного многочлена, то есть от необходимой точности (скорости сходимости к точному значению при уменьшении шага сетки) формулы. Коэффициенты представлены в таблице:

n	a 0	a 1	a 2	a 3	a 4	a 5	b
	− 1
	− 3		− 1
	− 11		− 9
	− 25		− 36		− 3
	− 137		− 300		− 75

Погрешность вычисляется по формуле

где h — шаг сетки, а точка ξ расположена где-то между i -тым и (i + n)-тым узлами. Примером может служить известная формула (n = 2)

.

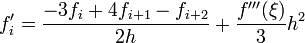При n = 1 формула может быть получена и из определения производной. Эта формула известна под названием формулы дифференцирования вперед.

Формулы «в конце таблицы» могут быть представлены в общем виде

в которых коэффициенты берутся из уже приведенной таблицы. В частности, при n = 1 получается известная формула дифференцирования назад.
14. Формулы численного дифференцирования методом неопределенных коэффициентов.

Другой способ построения формул численного дифференцирования приводит к тем же формулам - метод неопределённых коэффициентов. Чаще всего метод используется в многомерном случае, когда построить интерполяционный многочлен достаточно сложно. В этом случае коэффициенты численного дифференцирования ci выбираются из того, чтобы формула 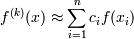была точна для многочленов максимально высокой степени. Пусть и потребуем, чтобы для такого многочлена соотношение для f(k)(x) обратилось в равенство: . Чтобы равенство выполнялось для любого многочлена степени m, необходимо и достаточно, чтобы коэффициенты при aj в правой и левой частях были равны (xj)(k) = j(j − 1)...(j − k + 1)xj − k. Получаем систему уравнений: относительно ci. Если m = n − 1, то число уравнений равно числу неизвестных. Определитель системы (определитель Вандермонда)отличен от нуля, то есть всегда можно построить формулу численного дифференцирования с n узлами, точную для многочленов степени n − i.
15. Наиболее распространенные формулы численного дифференцирования.

Дата добавления: 2015-04-24