Похибкa суми

Похибки арифметичних операцій

Теорема 1. Абсолютна похибка алгебраїчної суми декількох наближених чисел не перевищує суми абсолютних похибок цих чисел.

Доведення. Нехай x₁, x₂, …, х_п – задані наближені числа. Розгляне­мо їх алгебраїчну суму

и = ± х₁ ± х₂ ±... ± х_п.

Тоді похибка цієї алгебраїчної суми Дм буде складатися з алгебраїчної суми похибок доданків, тобто

∆ и = ± ∆ х₁ ± ∆ х₂ ±... ± ∆ х_п .

Звідси

|∆ и | ≤ |∆ х₁ | + |∆ х₂ | +... + |∆ х_п |.

Наслідок. За граничну абсолютну похибку алгебраїчної суми декількох наближених чисел можна прийняти суму граничних абсолютних похибок цих чисел, тобто

∆ _и = ∆ _х1 + ∆ _х2 +... + ∆ _хп .

Теорема 2. Гранична відносна похибка суми декількох наближених чисел одного й того ж знака не перевищує найбільшу з граничних відносних похибок цих чисел.

Доведення. Нехай

и = + х₁ + х₂ +... + х_п,

де для визначеності вважатимемо, що x _i > 0 (i = 1, 2,..., п). Позначимо

через А_i (і = 1, 2,..., п) точні значення доданків x _i , а через А – їх суму, тобто А = А₁ + + А₂ +... + А_п. Тоді

δ _u=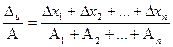

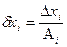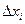Оскільки , то = А_і 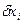. Тому

.

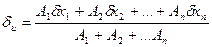Нехай

max = .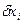

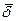1 ≤ i ≤ n

Тоді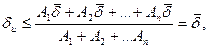

тобто 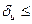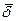= max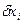

1 ≤ i ≤ n

2. Похибкa різниці. Розглянемо різницю двох наближених чисел х₁ та х₂:

и = х₁-х₂.

Тоді, на підставі наслідку з теореми 1,

∆ _и = ∆ _х1 + ∆ _х2, δ _u=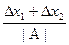

де А – точне значення різниці х₁-х₂. 3 останньої формули випливає, що для близьких чисел х₁ та х₂ гранична відносна похибка буде досить велика. Тому в обчислювальних алгоритмах бажано уникати віднімання близьких чисел.

Зауваження. При подальшому розгляді похибок арифметичних операцій, а також при розгляді похибок функцій припускатимемо, що похибки значно менші за абсолютною величиною від самих наближених величин, тож ними можна знехтувати в сумах, котрі містять одночасно наближену величину і її похибку як доданки; і завжди можна обмежитися членами, лінійними відносно похибок, нехтуючи членами більш високого порядку. Це означає, що наступні питання, пов'язані з похибками, розглядатимемо дещо грубо, проте елементарно. Адже строгий підхід під час розгляду цих питань не дає бажаних наочних результатів.

3. Похибкa добутку. Нехай

А_і=х_і+∆х_і (і = 1,2,..., n),

де для простоти вважатимемо, що х_і > 0 (і -1, 2,..., п), А = А ₁ А₂ … А_n, u = х₁х₂ … х_n . Тоді

А = (х₁ + ∆ х₁ ) (х ₂ + ∆ х₂) ... (х_п + ∆х_п) =

= х₁х₂ … х_n + х₂х₃ … х_n ∆ х₁ + х₁ х₃… х_n ∆ х₂ +... +

+ х₁х₂ … х_n-1 + ∆х_п +... + ∆x₁∆x₂…∆x_n.

Враховуючи зауваження, можемо прийняти, що

А = u +x₁ x₂ … х_п + ∆х₁+ х₁ х₃ … х_п + ∆х₂ +…+ x₁ x₂ … х_n-1 + ∆х_п.

Звідси

| ∆ u | = | А – u | ≤ x₂x₃ … x_n | ∆ x₁ | + х₁ х₃… x_n | ∆ x₂ | +…+

+ x₁ x₂ … х_n-1 + ∆х_п

Зокрема, якщо п = 2, то

| ∆ u | ≤ x₂ | ∆ x₁ | + x₁ | ∆ x₂ |.

За граничну абсолютну похибку добутку можна взяти

∆ u = x₂x₃ … x_n ∆ x₁+ х₁ х₃… x_n ∆ x₂ +…+ x₁ x₂ … х_n-1 + ∆х_п.

Розділивши нерівність на u, одержимо

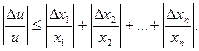
Враховуючи зауваження, замінюємо величину 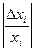на відносну

похибку 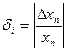множника х_i , а 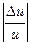– на відносну похибку

добутку 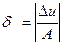. Отримаємо таку нерівність:

δ ≤ δ ₁ + δ ₂ + … δ _n.

За граничну відносну похибку добутку можемо прийняти

.

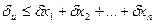4. Похибки частки. Нехай A₁ = х₁ + ∆ х₁, A₂ = х₂ + ∆ х₂, де для простоти x₁ > 0, x₂ > 0, 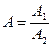, 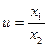. Тоді

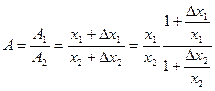
i

.

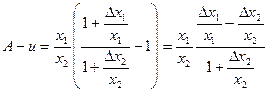Звідси

,

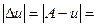
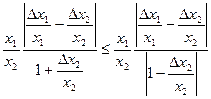aбo

.

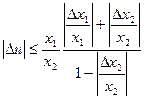Розділивши нерівність на u, одержимо

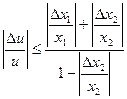
Врахувавши зауваження, замінимо 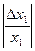на відносну похибку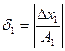

діленого, 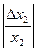- на відносну похибку 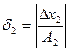дільника, 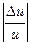- на відносну похибку 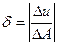частки. Отримаємо

.

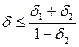За граничну відносну похибку частки можна прийняти

.

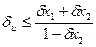5. Похибкa степеня. Нехай А = (х + ∆ х)^т, и = х^т, де т – нату­ральне число, х > 0. Використовуючи похибки добутку, одержуємо

|∆ u | < mx^{m - 1} |∆ x |, δ ≤ mδ₁,

де δ – відносна похибка степеня; δ₁ – відносна похибка аргументу х. Тому за граничні абсолютну та відносну похибки степеня можемо прийняти

∆ _u= mx^{m - 1} ∆ x, δ _u= mδ _x.

Із наведених похибок арифметичних операцій випливає, що операції додавання та віднімання (при великій різниці між числами) не погіршують точності результату порівняно з точністю алгебраїчних доданків, а операції множення, ділення і піднесення до степеня суттєво погіршують точність результату.

Дата добавления: 2015-05-23