Узагальнений закон Гука

Одержимо вираз для вільної енергії F як функції компонентів тензора деформацій, потім по формулі (75) встановимо зв'язок між компонентами тензора напружень і тензора деформацій.

Скориставшись малістю деформацій, розкладемо вільну енергію в ряд по ступенях 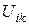в околиці точки .

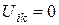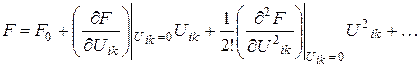(76)

Під час відсутності зовнішніх сил і під час відсутності деформації тіла, тобто при 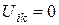, дорівнюють нулю і внутрішні напруження, .

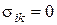Але . Виходить,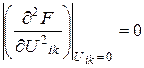

Вище ми бачили (формула (44)), що

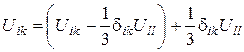
Отже, можна записати:

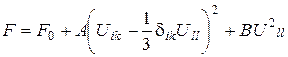
Дійсно, після зведення виразу для в квадрат і підстановки в (76) залишаться лише члени типу 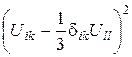і 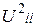, тому що 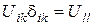і 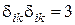. А й B - деякі константи, що є коефіцієнтами при таких членах.

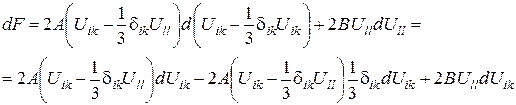
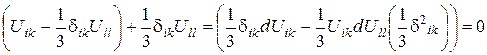
(77)

Для визначення констант А й В звернемося до окремих випадків. У випадку чистого зсуву дотичні напруження виражаються формулами для чистого зсуву

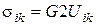
де G - модуль зсуву. Таким чином, 2 A = 2 G, A = G.

У випадку всебічного стиснення з (77) для нормальних напружень одержуємо вираз

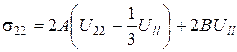
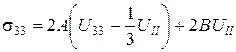
З іншої сторони Закон Гука для всебічного стиснення матеріалу під тиском Р має вигляд:

,

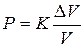де K - коефіцієнт всебічного стиснення, а 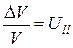, тобто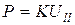

Очевидно, у випадку всебічного стиснення

; .

;

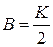
Підстановка отриманих для А й В значень у (77) призводить до співвідношення

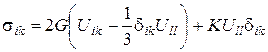(78)

Це і є узагальнений закон Гука для ізотропного тіла. Можна одержати аналогічний вираз, що представляє тензор деформацій через тензор напружень:

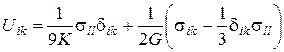(79)

Необхідно відзначити, що модуль зсуву і модуль всебічного стиснення, уведені нами просто як коефіцієнти в розкладанні вільної енергії пружно деформованого тіла по компонентах тензора деформацій, вони дійсно зв'язані, один - з деформацією всебічного стиску, а інший - з деформацією чистого зсуву. Це видно з формули (78), у якій K є коефіцієнтом при сумі діагональних компонентів тензора деформацій .

Сума є відносною зміною об’єму при деформації і не містить у собі деформацій, зв'язаних зі зміною форми елементів об’єму тіла, що деформується, у той же час коефіцієнт G збільшується в (78) на таку комбінацію, утворену з компонентів тензора деформацій, що являє собою деформацію чистого зсуву.

Встановимо, як зв'язані модуль всебічного стиснення і модуль зсуву з модулем Юнга та з коефіцієнтом Пуассона, (відношення відносного поперечного звуження до відносного подовжнього подовження при одновісному пружному розтязі матеріалу).

З цією метою розглянемо окремий випадок пружної деформації - одновісний розтяг.

Рис.16. Деформація одновісного розтягу

За визначенням, модулем Юнга E називається, коефіцієнт, що зв'язує в цьому випадку законом пропорційності напруження 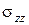і відносне подовження в напрямку осі Z.

(80)

Коефіцієнт Пуассона 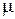, знову таки по визначенню, входить у співвідношення:

чи

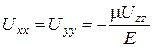(81)

Знак "-" вказує на те, що в поперечному напрямку відбувається стиснення матеріалу.

З узагальненого закону Гука (79) для діагональних компонентів тензора деформацій 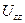і 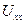в розглянутому випадку виходить:

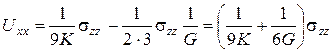
Порівнюючи ці співвідношення з формулами (80) і (81), безпосередньо знаходимо:

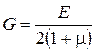(83)

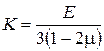(84)

Зворотні співвідношення, як можна переконатися, перетворюючи (83) і (84), мають вигляд:

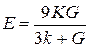(85)

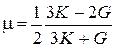(86)

Відповідно до отриманих формул тензор напружень виражається через тензор деформації наступним чином:

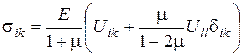(87)

Тензор деформацій - через тензор напружень:

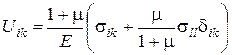(88)

Зрозуміло, (87) і (88) також являють собою узагальнений закон Гука для ізотропного тіла.

Дата добавления: 2015-05-24