
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нехай маємо послідовність
|
|
|
|
 (1.1)
(1.1)
елементами якої є точки метричного простору Х.
Означення 1.5. Точка  , метричного простору Х, називається границею послідовності (1.1), якщо
, метричного простору Х, називається границею послідовності (1.1), якщо 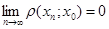 .
.
Дане означення, очевидно еквівалентне наступному:
Означення 1.5.* Точка  є границею послідовності (1.1), якщо
є границею послідовності (1.1), якщо  $ NÎ N, таке, що для всіх n≥N, виконується нерівність
$ NÎ N, таке, що для всіх n≥N, виконується нерівність  .
.
Якщо  є границею послідовності (1.1), то це записують так:
є границею послідовності (1.1), то це записують так:  .
.
Як ми бачимо, означення границі послідовності в метричному просторі, аналогічне означенню границі послідовності дійсних чисел (Якщо  , то
, то  ).
).
Якщо  , то геометрично це означає, що який би ми окіл точки
, то геометрично це означає, що який би ми окіл точки  не взяли, починаючи з деякого номера, всі члени послідовності попадуть в цей окіл.
не взяли, починаючи з деякого номера, всі члени послідовності попадуть в цей окіл.
Означення 1.6. Послідовність, яка має границю, називається збіжною.
Теорема 1.1. Якщо послідовність має границю, то вона єдина.
Доведення. Нехай  і
і  . Поскільки
. Поскільки 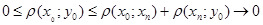 ,коли
,коли 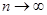 , то
, то  . Зачить
. Зачить 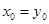 .
.
Теорема 1.2. Якщо послідовність  має границю,
має границю,  , то і будь-яка її підпослідовність
, то і будь-яка її підпослідовність 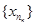 має границю
має границю  .
.
Доведення. Нехай  . Тоді
. Тоді  , на основі властивості границі для послідовностей дійсних чисел
, на основі властивості границі для послідовностей дійсних чисел 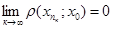 , де
, де  – підпослідовність послідовності
– підпослідовність послідовності  .
.
Теорема 1.3. Якщо послідовність має границю, товона – обмежена.
Доведення. Нехай  . Візьмемо
. Візьмемо 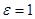 , тоді існує натуральне число N таке, що при всіх
, тоді існує натуральне число N таке, що при всіх  виконується нерівність:
виконується нерівність:
 (1.2).
(1.2).
Нерівність може не виконуватись тільки для перших N -1 елементів цієї послідовності. Якщо за r візьмемо  , то для всіх n виконується нерівність:
, то для всіх n виконується нерівність: 
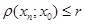 .
.
Означення1.7. Нехай маємо послідовність  елементів метричного простору Х. Дана послідовність називається фундаментальною, якщо
елементів метричного простору Х. Дана послідовність називається фундаментальною, якщо  $ NÎ N таке, що при всіх n≥N, m≥N виконується нерівність
$ NÎ N таке, що при всіх n≥N, m≥N виконується нерівність  .
.
Tеорема 1.4. Якщо послідовність  має границю, то вона – фундаментальна.
має границю, то вона – фундаментальна.
Дана теорема доводиться аналогічно, як і для послідовностей дійсних чисел.
|
|
|
Обернене твердження, як це було для дійсних чисел, в довільному метричному просторі не вірне. Дійсно, розглянемо простір, елементами якого є раціональні числа і відстань між х і у визначимо рівністю 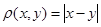 . Послідовність
. Послідовність  , nÎ N належить цьому простору, вона – фундаментальна, але границі не має (
, nÎ N належить цьому простору, вона – фундаментальна, але границі не має ( ірраціональне число).
ірраціональне число).
Лема 1.1. Для будь-яких x, y, z, u з метричного простору Х правильна нерівність:
 (1.3).
(1.3).
Доведення. За аксіомою трикутника маємо
 ,
,
звідси
 (1.4).
(1.4).
Помінявши місцями x i z, y i u, одержимо:
 (1.5).
(1.5).
З (1.4) і (1.5) випливає (1.3). Лему доведено.
Теорема 1.5. Коли  ,
,  , то
, то  .
.
Доведення. За лемою 1.1  , коли
, коли 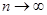 . Теорему доведено.
. Теорему доведено.
Нехай маємо лінійний нормований простір. Тоді в цьому просторі можемо ввести метрику, поклавши  . Збіжність в метриці породженій нормою, називають збіжністю по нормі.
. Збіжність в метриці породженій нормою, називають збіжністю по нормі.
Теорема 1.6. Якщо послідовність  фундаментальна і існує підпослідовність
фундаментальна і існує підпослідовність  цієї послідовності, яка збігається до
цієї послідовності, яка збігається до  , то і сама послідовність збігається до
, то і сама послідовність збігається до  .
.
Доведення. Нехай  фундаментальна послідовність,
фундаментальна послідовність,  – збіжна підпослідовність,
– збіжна підпослідовність,  . Візьмемо
. Візьмемо 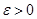 . Внаслідок фундаментальності
. Внаслідок фундаментальності  , існує натуральне число N 1 таке, що при
, існує натуральне число N 1 таке, що при  , виконується нерівність:
, виконується нерівність:
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 1105; Нарушение авторских прав?; Мы поможем в написании вашей работы!