Розділ 2. Диференційовність функцій багатьох змінних

.

А це означає, що складна функція неперервна в точці t⁽⁰⁾. Теорему доведено.

Оскільки дана функція має множину значень, яка є деякою множиною дійсних чисел, які можна порівнювати, то виникає питання: чи має місце тут теорема Больцано-Коші?

Теорема 1.4. Больцано-Коші (для функції багатьох змінних.)

Нехай f:E®R неперервна на зв’язній множині ЕÌRⁿ. Якщо f(x^{( 1 )} )=A, f(x ⁽²⁾ )=B; x^{( 1 )} , x⁽²⁾ÎE, A¹B, то для будь-якої точки C,(CÎR), що лежить між А і В, існує точка х ⁽³⁾ ÎЕ така, що f(x⁽³⁾)=C.

Доведення. Оскільки Е зв’язна множина в Rⁿ, то за теоремою 1.1, будь-які дві її точки можна з’єднати неперервною кривою, всі точки якої належать множині Е. Це означає, що неперервною кривою можна з’єднати і точки х⁽¹⁾, х⁽²⁾, де х^{( 1 )} =(х ₁ ^{( 1 )} , х₂^{( 1 )} ,..., х_п^{( 1 )} ), х⁽²⁾=(х ₁⁽²⁾, х₂ ⁽²⁾ ,..., х_п ⁽²⁾).

Таким чином існують функції х ₁ =j ₁ (t), х₂=j₂(t),…, х_n=j_n(t), –неперервні на [ a,b ], (j ₁ (a)…j_n(a))=x^{( 1 )} , (j ₁ (b)…j_n(b))=x ⁽²⁾іякщо t змінюється від a до b, то точка рухається по цій кривій від х^{( 1 )} до х⁽²⁾.

Розглянемо нашу функцію в точках тільки цієї неперервної кривої. Оскільки точки кривої задаються системою рівнянь від змінної t, z=f(x ₁, x₂,…,x_n), а точки (x ₁, x₂,…,x_n) належать кривій, то х ₁ =j ₁ (t), x₂=j₂(t),…, x_n=j_n(t). Це означає, що наша функція z є складною функцією параметра t, z=f(j ₁ (t),j₂(t),…,j_n(t)), tÎ [ a,b ]= Y (t).

Y(a)=A, Y(b)=B.

Оскільки f неперервна на Е, то вона неперервна в точках кривої, що належить цій множині. Кожний аргумент х_і, теж є неперервною функцією параметра t. Тому за теоремою 1.2, матимемо, що складна функція Y(t) є неперервною функцією однієї змінної на [ a, b ], а звідси за теоремою Больцано-Коші (з одномірного аналізу) випливає, що існує gÎ [ a, b ]: Y(g)=C (з умови теореми), тобто f(j₁(g), j₂(g),…, j_n(g))=C, а оскільки точка (j₁(g), j₂(g),…, j_n(g)) є точкою нашої кривої, то вона є і точкою множини Е, позначимо її х⁽³⁾. Таким чином f(x⁽³⁾)=С. Теорему доведено.

Приведемо ще одне різницеве означення неперервності функції багатьох змінних.

Означення 1.4. Нехай U=f(x₁,…,x_n) – задана в деякій області G, і (х ₁ ⁽⁰⁾,х ₂ ⁽⁰⁾,...,х_п⁽⁰⁾)ÎG. Надамо цій точці приріст, так щоб новоутворена точка не

вийшла за межі області G. Одержимо точку 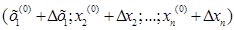. Тоді величина 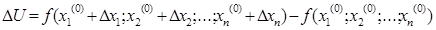, називається приростом функції f(x ₁; x₂;…;x_n).

Зрозуміло, що функція U=f(x ₁ ,…,x_n) буде неперервною в точці (x ₁⁽⁰⁾ ,…,x_n⁽⁰⁾) тоді і тільки тоді, коли .

Дата добавления: 2015-05-24