Другие термины и понятия

Классификация игр

Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функции выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры.

1) Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков более двух.

2) Игра называется с нулевой суммой или антагонистической, если выигрыш одного из игроков равен проигрышу другого. Игры с постоянной разностью – игроки выигрывают и проигрывают одновременно.

3) Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной – в противном случае.

4) Бескоалиционными называются игры, в которых игроки не имеют права вступать в соглашения, образовывать коалиции. В коалиционной игре, наоборот, игроки могут вступать в соглашения и образовывать коалиции. В кооперативной игре коалиции определены заранее, то есть до начала игры игроки могут принимать соглашения о своих стратегиях (возможность предварительных переговоров). В некооперативной игре игроки не могут координировать свои стратегии подобным образом и принимают решения независимо друг от друга.

5) Комбинаторные игры: число исходов, стратегий, факторов конечное, не очень большое. Можно построить модель игры, выработать правила. Однако численное решение невозможно из-за большой размерности задачи. В случайных играх количество исходов не зависит от поведения игрока. В стратегических играх один участник находится в состоянии неопределенности относительно поведения других участников игры.

6) Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаются выигрыши первого игрока в виде матрицы. Любая матричная игра имеет решение и может быть реализована методами линейного программирования. Матричные игры еще называют играми в нормальной форме. Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой есть матрицы выигрышей (проигрышей) отдельно для каждого участника. Непрерывной считается игра, в которой функция выигрышей является непрерывной в зависимости от стратегий.

Выбор и осуществление одного из предусмотренных правилами действий называется ходом игрока. Ходы могут быть личными и случайными. Личный ход – это сознательный выбор игроком одного из возможных действий. Случайный ход – это случайно выбранное действие (выбор карты из перетасованной колоды).

Стратегией игрока называется совокупность правил, определяющих выбор действия при каждом ходе в зависимости от сложившейся ситуации. Чтобы решить игру или найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, то есть один из игроков получает максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными.

Оптимальные стратегии должны удовлетворять условию устойчивости, то есть любому из игроков должно быть невыгодно отказываться от своей стратегии в этой игре. Если игра повторяется много раз, то игроков может интересовать не выигрыш и проигрыш в каждой конкретной партии, а средний выигрыш (проигрыш) во всех партиях.

Целью теории игр является определение оптимальной стратегии для каждого игрока.

Выигрыш – это мера эффекта для игрока. В теории игр выигрыш должен измеряться обязательно количественно.

В случае конечной игры двух лиц функции выигрыша каждого из игроков удобно представлять в виде матрицы выигрышей, где строки представляют собой стратегии одного игрока, а столбцы – стратегии другого. В клетках матрицы указываются выигрыши каждого из игроков в каждой из образующихся ситуаций. Данная форма представления конечных игр называется «матричные игры».

Пример решения задачи. Игра в «орлянку».

Если оба выбирают одинаковые стратегии (оба говорят “орел”), то 1-й выигрывает 1 рубль (а второй проигрывает); если выбирают разные, то 2-й выигрывает.

Таблица 2.1

Матрица выигрыша первого игрока (Н₁)

	Орел	Решка
Орел		–1
Решка	–1

Матрица выигрыша второго игрока (Н₂)

	Орел	Решка
Орел	–1
Решка		–1

Для антагонистических игр всегда Н₁= – Н₂.

Матрица, элементами которой являются выигрыши, соответствующие стратегиям игроков, называется платежной матрицей или матрицей игры.

Нижняя цена игры (α) (максиминный выигрыш – максимин) – это гарантированный выигрыш первого игрока при любой стратегии второго игрока (то есть из каждой строки выбираем минимальное число, а затем из всех этих минимумов берем наибольший). Стратегия, соответствующая максимину называется максиминной.

Верхняя цена игры (β) (минимаксный выигрыш – минимакс) – это гарантированный проигрыш второго игрока. (То есть из каждого столбца выбираем максимальное число, а затем из всех максимумов берем наименьший). Стратегия, соответствующая минимаксу, называется минимаксной.

Принцип, диктующий игрокам выбор наиболее «осторожных» минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника. Если верхняя и нижняя цены игры совпадают α=β= , то эта цена называется чистой ценой игры или ценой игры.

Для А=

Для В=

Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями или решением игры. То есть в этом случае первый игрок получает максимальный, не зависящий от поведения второго игрока выигрыш q, а второй игрок добивается минимального гарантированного, не зависящего от поведения первого игрока проигрыша q. Такое решение обладает устойчивостью, то есть если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Пара стратегий дает оптимальное решение игры тогда и только тогда, когда соответствующий элемент матрицы (размер выигрыша-проигрыша) является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация, если она существует, называется седловой точкой. То есть игра разрешима в чистых стратегиях, каждый из игроков будет на каждом шаге выбирать одну и ту же стратегию и ему не выгодно от нее отклониться: если первый игрок выберет другую стратегию, у него будет выигрыш меньше, а если второй игрок выберет другую стратегию, у него проигрыш будет больше.

Пример решения задачи.

Определить верхнюю и нижнюю цену игры, заданной платежной матрицей. Имеет ли игра седловую точку?

Р=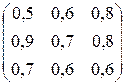

Таблица 2.2

Платежная матрица игры

	B1	B2	B3	α
A1	0,5	0,6	0,8	0,5
A2	0,9	0,7	0,8	0,7
A3	0,7	0,6	0,6	0,6
β	0,9	0,7	0,8	0,7

– цена игры. Седловая точка (А₂, В₂).

Пример решения задачи. Рассмотрим две конкурирующие финансовые компании А и В. Компания В ведёт переговоры с организаторами каждого из трёх проектов В ₁ , В ₂ , В ₃ на предмет инвестирования. Задача компании В: положительный результат переговоров. Компания А ставит своей задачей свести переговоры компании В к отрицательному результату, с тем чтобы занять место компании В в инвестировании.

Компания А для достижения своей цели – срыва переговоров компании В – может применить одно из двух средств: А ₁ – предложить организаторам проектов более выгодные для них условия инвестирования по сравнению с компанией В и А ₂ – предоставить в распоряжение организаторов проектов материалы, компрометирующие компанию В.

Действие А ₁ компании А приводит к отрицательному результату переговоров компании В с организаторами проектов В ₁ , В ₂ , В ₃, соответственно, с вероятностями 0,7; 0,5; 0,3, а действие А ₂ – с вероятностями 0,6; 0,9; 0,4.

Решение. Смоделируем данную ситуацию. Поскольку компании А и В преследуют противоположные цели, то рассматриваемая конфликтная ситуация является антагонистической. Игроками являются финансовые компании А и В. Игрок А имеет две чистые стратегии А ₁ и А ₂: ; множество стратегий игрока В состоит из трёх стратегий: . Игрок В должен выбрать один из трех проектов, игрок А выбирает одно из двух своих действий.

В качестве выигрыша игрока А (или проигрыша игрока В) рассмотрим вероятность отрицательного результата переговоров компании В. В соответствии со своими задачами игрок А стремится максимизировать выигрыш, а игрок В – минимизировать проигрыш.

Выясним, имеет ли игра седловую точку, то есть, разрешима ли игра в чистых стратегиях.

Матрица игры с показателями эффективности стратегий А ₁ , А ₂ и показателями неэффективности стратегий В ₁ , В ₂ , В ₃ имеет следующий вид:

Таблица 2.3

Платежная матрица игры

Bj Ai	B 1	B 2	B 3	α
A 1	0,7	0,5	0,3	0,3
A 2	0,6	0,9	0,4	0,4
β	0,7	0,9	0,4	0,4 0,4

В данном случае максиминной стратегией игрока А является стратегия А ₂ , а минимаксной стратегией игрока В – стратегия В ₃.

Если игрок А придерживается своей максиминной стратегии А ₂ , то игрок В должен выбрать свою минимаксную В ₃, с тем чтобы выигрыш игрока А (или что то же – проигрыш игрока В) был минимальным а ₂₃ = 0,4 (во 2-й строке матрицы (6.1)). На это игрок А должен ответить выбором опять же стратегии А ₂ , чтобы получить максимальный (в 3-м столбце) выигрыш: а ₂₃ = 0,4. Ответным ходом игрок В опять выбирает стратегию В ₃ и т. д.

Таким образом, если игроки А и В придерживаются своих максиминной и минимаксной стратегий, то ни один из них не может увеличить свой выигрыш, отступая от своей стратегии. Ситуация (А ₂ , В ₃) является в данной игре устойчивой.

Нижняя и верхняя цены игры совпадают:

a = b = 0,4

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_A игрока А называется применение чистых стратегий А₁, А₂,…..А_i, …., А_m с вероятностями p₁, p₂,…., p_i,….,p_m, причем сумма вероятностей равна 1: . Цена игры будет удовлетворять неравенству .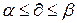

Основная теорема теории игр – теорема Неймана. Каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

В качестве примеров применения теории можно назвать решения по поводу проведения принципиальной ценовой политики, выхода на новые рынки, кооперации и создания совместных предприятий, определения лидеров и исполнителей в области инноваций, вертикальной интеграции и т.д. Положения данной теории в принципе можно использовать для всех видов решений, если на их принятие влияют другие действующие лица. Этими лицами, или игроками, необязательно должны быть рыночные конкуренты; в их роли могут выступать субпоставщики, ведущие клиенты, сотрудники организаций, а также коллеги по работе.

2.3. Геометрическая интерпретация игры 2´2

Пусть имеется два игрока А и В. У каждого из игроков по две стратегии (А₁ и А₂ у игрока А, В₁ и В₂ у игрока В). Игра с нулевой суммой.

По оси абсцисс отложим отрезок А₁А₂, то есть точка А₁ изображает стратегию А₁ (х=0), А₂ – стратегию А₂, все промежуточные точки – смешанные стратегии. На оси ординат откладываем выигрыш первого игрока, если второй применил стратегию В₁. Аналогично строим второй график, если второй график выбрал стратегию В₂.

Рис. 2.1. Геометрическая интерпретация стратегий первого игрока

q₁₌a₁₁p₁+a₂₁p₂

q₂=a₁₂p₁+a₂₂p₂ (ордината точки М₁ и М₂, соответственно)

В соответствии с принципом минимакса оптимальная стратегия S_А^* такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум.

Рис. 2.2. Решение игры графическим способом

Отрезок В₁N – минимальный выигрыш игрока А при использовании любой смешанной стратегии, если игрок В выбрал стратегию В₁. Аналогично, отрезок В₂N – выигрыш игрока А, если игрок В выбрал стратегию В₂. Следовательно, оптимальную стратегию определяет точка N, то есть минимальный выигрыш достигает максимума.

Пример решения задачи.

Решить графически игру, заданную платежной матрицей:

Р=

Определим верхнюю и нижнюю цены игры: 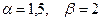. Следовательно, седловая точка отсутствует, будем искать решение в смешанных стратегиях. Отметим на графике величину выигрыша для каждой пары стратегий.

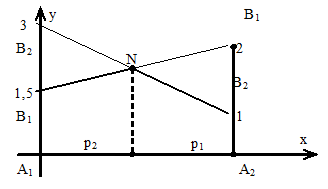
Рис. 2.3. Графическое решение игры

Запишем уравнение прямых, соответствующих величине выигрыша игрока А, если игрок В выбирает, соответственно, первую (B₁) y= = 0,5 x + 1,5 и вторую (B₂) y= –2x + 3 стратегии. Точка их пересечения N(0,6; 1,8). Следовательно, р₂ = x = 0,6 – вероятность выбора игроком А второй стратегии; р₁ = 1 – 0,6 = 0,4 – вероятность выбора игроком А первой стратегии. Цена игры = y = 1,8 – максимально возможный из минимально гарантированных выигрышей игрока А (либо минимально возможный из максимально гарантированных проигрышей игрока В).

Ø Важно помнить. Графически можно решить игру, если в игре участвуют только два игрока и у одного из игроков имеется только две стратегии (у второго игрока – любое количество стратегий).

Задания для самостоятельной работы.

1. Для этой же задачи начертить график, записать уравнения прямых, найти вероятности и седловую точку для игрока В.

2. Применив методы теории игр, найти пропорцию использования посевной площади для производства трех сортов пшеницы, урожайность которых зависит от погодных условий. Критерий оптимальности – максимум валового урожая. Решить задачу графически.

Таблица 2.4

Размер урожайности каждого сорта в зависимости погодных условий

	Засушливый год	Нормальный год	Дождливый год
Сорт 1
Сорт 2
Сорт 3

3. Игрок А записывает одно из двух чисел: 2 или 3. Игрок В записывает одно из трех чисел: 3, 4 или 5. Если числа одинаковой четности, то А выигрывает сумму чисел; и если четности чисел не совпадают, то сумму чисел выигрывает В. Построить платежную матрицу игры, определить верхнюю и нижнюю цену игры. Проверить наличие седловой точки.

Рассмотрим ситуацию, когда игра разрешается в чистых стратегиях, т. е. есть седловая точка. Графическое решение задачи может иметь следующие виды.

Рис. 2.4. Графики игр, разрешимых в чистых стратегиях

Дата добавления: 2015-05-09