Разложение вектора по данному базису

ЛИНЕЙНОЕ ПРОСТРАНСТВО. РАЗМЕРНОСТЬ, БАЗИС.

Пусть мы имеем некоторое множество , для элементов которого установлены понятия равенства 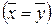, операции сложения ( - сумма элементов) и умножения на число 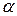( 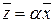или - произведение элемента 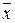на число 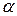), обладающие следующими свойствами:

1) ;

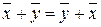2) ;

3) В множестве имеется элемент такой, что для любого , его называют нулевым элементом.

4) Для любого элемента имеется элемент такой, что 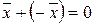, его называют противоположным элементу .

5) ;

6) ;

7) ;

8) .

Множество с определенными для его элементов операциями сложения и умножения на число, удовлетворяющими аксиомам 1-8, называется линейным (или векторным), а его элементы – векторами.

Линейными пространствами будут:

1. Множество всех векторов, принадлежащих некоторой плоскости.

2. Множество всех векторов, принадлежащих трехмерному пространству.

3. Множество всех 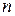-векторов.

Если некоторый вектор 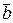линейного пространства представлен в виде линейной комбинации векторов того же пространства, т.е.

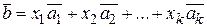, (3.1.)

то говорят, что вектор 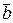разложен по векторам .

Важную роль в теории пространств играет понятие линейной зависимости и независимости векторов. Равенство (3.1) при 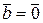представляет разложение нуль-вектора по векторам

(3.2.)

Такое разложение всегда можно. Значит линейная независимость системы векторов означает, что разложение нуль-вектора по векторам системы возможно единственным образом.

Максимально возможное число линейно независимых векторов в конечномерном пространстве называется размерностью этого пространства.

Множество 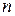-мерных векторов образует 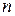-мерное пространство, которое обозначается через .

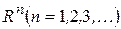Система 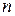линейно независимых векторов в 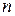– мерном пространстве называется базисом этого пространства.

Пусть вектора , их компоненты обозначим 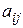: первый индекс () – номер координаты данного вектора, второй индекс () – номер вектора в системе,

.

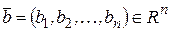В силу определения равенства векторов и операций сложения и умножения вектора на число в 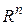, векторное равенство (3.1) теперь можно записать в виде системы 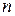линейных уравнений с неизвестными:

(3.3.)

Координаты вектора 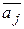образуют столбец коэффициентов при переменной , а координаты вектора 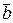- столбец свободных членов. Обратно, если в произвольно заданной системе (3.3) совокупность коэффициентов при одной и той же переменной и свободные члены рассматривать как соответствующие 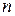-мерные векторы, то мы придем к векторному уравнению (3.1).

Уравнение (3.1) называют векторной формой записи системы линейных уравнений (3.3).

В частности, уравнение (3.2) является векторной формой записи однородной системы линейных уравнений

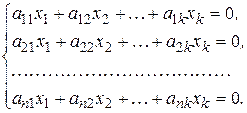(3.4)

Система (3.4) всегда совместна, если это решение единственное, то равенство (3.2) имеет место только при , т.е система векторов линейно независима.

Система (3.4) будет иметь единственное нулевое решение тогда и только тогда, когда ее ранг равен числу переменных 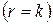, т.е. ранг основной матрицы системы:

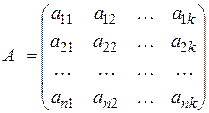, (3.5)

столбцы которой образованы компонентами этих векторов, равен числу ее столбцов.

Так как 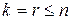, т.е. в пространстве 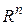система линейно независимых векторов не может содержать более 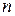векторов.

Любые 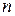векторов , для которых определитель со столбцами, образованными координатами векторов,

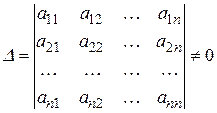(3.6)

будут линейно независимыми, и образуют базис этого пространства.

Переход от старого базиса к новому задается матрицей перехода

, (3.7)

где первый индекс -номер координаты вектора, второй индекс -номер вектора нового базиса, так что

. (3.8)

Переход от координат вектора 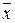относительно старого базиса к координатам относительно нового базиса осуществляется по формуле

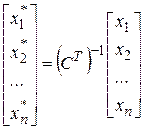. (3.9)

Пример 3.1. В базисе 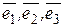заданы векторы , 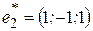и 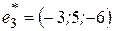. Показать, что векторы образуют базис. Вектор 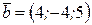, заданный в базисе 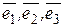разложить в базисе .

Решение. Составим матрицу перехода от старого базиса к новому

Дата добавления: 2015-05-26