Уравнение прямой, проходящей через две заданные несовпадающие точки

Уравнение прямой в отрезках

Уравнение прямой с угловым коэффициентом

Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке 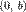и образующая угол с положительным направлением оси Ox:

Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.

Способы задания прямой:
или

Прямая линия, пересекающая ось Ox в точке 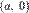и ось Oy в точке :

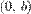В этом виде невозможно представить прямую, проходящую через начало координат.

Уравнение прямой, проходящей через две заданные несовпадающие точки и

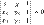
или

или в общем виде

68. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой

Две прямые, заданные уравнениями

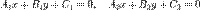
или

Эти прямые параллельны, если A ₁ B ₂ − A ₂ B ₁ = 0 или k ₁ = k ₂, и

перпендикулярны, если A ₁ A ₂ + B ₁ B ₂ = 0 или

Расстояние точки A (x ₁, y ₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

69. Декартова система координат. Способы задания поверхностей. Общее уравнение поверхности в пространстве.

ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т, прямолинейная система координат на плоскости или в пространстве (обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям). Названа по имени Р. Декарта (см. ДЕКАРТ Рене).
Декарт впервые ввел координатную систему, которая существенно отличалась от общепринятой в наши дни. Для задания декартовой прямоугольной системы координат выбирают взаимно перпендикулярные прямые, называемые осями. Точка пересечения осей O называется началом координат. На каждой оси задается положительное направление и выбирается единица масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P.

Метод задания поверхности каркасом линии называется каркасным.

Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать внутренние свойства поверхности. При проектировании поверхностей технических форм и их воспроизведении на станках с программным управлением используются совместно графические и аналитические способы задания поверхностей.

Поверхности рассматривают как множество точек и линий. Координаты точек этого множества удовлетворяют некоторому заданному уравнению вида F(x, y, z) = 0.

Алгебраической поверхностью n-го порядка называется поверхность, уравнение которой – алгебраическое уравнение степени n.

Графический способ задания поверхностей.

Способы аналитического задания

1. - векторно-параметрическое уравнение.

2. - параметрические уравнения.

3. 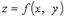- явное уравнение.

4. - неявное уравнение.

Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности. Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

Рассмотрим точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) в общей декартовой системе координат. Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы 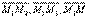были компланарны. ( ) = 0 Таким образом, 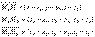Уравнение плоскости, проходящей через три точки:

70. Общее уравнение плоскости в пространстве. Уравнение плоскости в отрезках

Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению:

Ax + By + Cz + D = 0,

где А, В, С – координаты вектора -вектор нормали к плоскости.

Возможны следующие частные случаи:

А = 0 – плоскость параллельна оси Ох

В = 0 – плоскость параллельна оси Оу

С = 0 – плоскость параллельна оси Оz

D = 0 – плоскость проходит через начало координат

А = В = 0 – плоскость параллельна плоскости хОу

А = С = 0 – плоскость параллельна плоскости хОz

В = С = 0 – плоскость параллельна плоскости yOz

А = D = 0 – плоскость проходит через ось Ох

В = D = 0 – плоскость проходит через ось Оу

С = D = 0 – плоскость проходит через ось Oz

А = В = D = 0 – плоскость совпадает с плоскостью хОу

А = С = D = 0 – плоскость совпадает с плоскостью xOz

В = С = D = 0 – плоскость совпадает с плоскостью yOz

Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

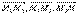Рассмотрим точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) в общей декартовой системе координат. Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы были компланарны. ( ) = 0 Таким образом, Уравнение плоскости, проходящей через три точки:

71. Условие параллельности и перпендикулярности плоскостей. Нормальное уравнение плоскости.

Дата добавления: 2015-05-26