
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Точность оценки регрессии
|
|
|
|
Классическая модель нормальной линейной регрессии
Коэффициент частной корреляции
Если исследуется зависимость между тремя величинами x, в, z (спрос на бензин, цены, доход) и нужно выделить влияние которых или два факторов, то используется так называемый коэффициент частной корреляции  - коэффициент частной корреляции между в и х в случае постоянства действия величины z
- коэффициент частной корреляции между в и х в случае постоянства действия величины z
 - обычные коэффициенты корреляции.
- обычные коэффициенты корреляции.
Коэффициент корреляции показывает, что две переменные связаны друг с другом, однако он не дает представления о том, каким образом они связаны.
Рассмотрим классическую линейную модель регрессии.
 , (1)
, (1)
то есть наблюдаемая случайная величина В (регрессанд, зависимая переменная, объяснимая переменная) представляется в виде линейной функции от к наблюдаемым переменным (регрессоров, независимых переменных, объясняющих переменных)  и от скрытых (=латентных =неявных) случайных переменных U (=возмущений уравнений =случайных возмущений).
и от скрытых (=латентных =неявных) случайных переменных U (=возмущений уравнений =случайных возмущений).
Основные предпосылки нормальной классической линейной модели регрессии
Модель (1) называется классической если выполняются следующие предпосылки (предположение):
1. регрессоры 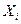 являются не случайными, а детерминированными, то есть их значение можно контролировать. Это значит, что экспериментатор может в лабораторном эксперименте произвольно задавать значение регрессоров. Эта предпосылка является нереальной для многих прикладных регрессионных моделей в экономике и социологии. Здесь в группу регрессоров часто включают стохастические неконтролированные величины (например, цены и количество предлагаемых или таких, которые имеют спрос товаров). С обобщениями классической модели, которые учитывают нарушение этой предпосылки, мы ознакомимся позже.
являются не случайными, а детерминированными, то есть их значение можно контролировать. Это значит, что экспериментатор может в лабораторном эксперименте произвольно задавать значение регрессоров. Эта предпосылка является нереальной для многих прикладных регрессионных моделей в экономике и социологии. Здесь в группу регрессоров часто включают стохастические неконтролированные величины (например, цены и количество предлагаемых или таких, которые имеют спрос товаров). С обобщениями классической модели, которые учитывают нарушение этой предпосылки, мы ознакомимся позже.
|
|
|
2. Единственной случайной переменной в (1) есть 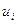 и следовательно, зависимая от нее
и следовательно, зависимая от нее  . Возмущения делают регрессионную функцию стохастической.
. Возмущения делают регрессионную функцию стохастической.
Предусматривается, что для возмущений (остатков) выполняются условия Гаусса-маркова:
2.1 Возмущение (остаток)  является случайной величиной со средним, ровным нулю, и дисперсией (
является случайной величиной со средним, ровным нулю, и дисперсией ( неизвестной), то есть
неизвестной), то есть
2.2 Остатки 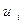 и
и  при
при 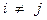 некоррелируемые, так что
некоррелируемые, так что  .
.
Поэтому 
Значение  и
и  некоррелируемые при
некоррелируемые при 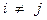

2.3 Остаток 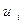 нормально распределен случайная величина со средним значением ровным нулю и дисперсией, то есть.
нормально распределен случайная величина со средним значением ровным нулю и дисперсией, то есть.
При добавлении этого предположения остатки 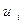 и
и  становятся не только некоррелируемыми, но и обязательно независимыми.
становятся не только некоррелируемыми, но и обязательно независимыми.
Если все эти предпосылки выполняются, то такая модель называется классической линейной моделью нормальной регрессии. Если не выполняется предпосылка 2.3 относительно нормального распределения возмущений, то имеет место классическая линейная регрессионная модель.
Предусматривается, что каждое наблюдение отзыва В имеет нормальное распределение относительно вертикали со средним, получаемым из постулированной модели. Дисперсии же всех нормально распределенных величин предусматриваются одинаковыми и ровными.
Во многих реальных ситуациях ошибки, в соответствии с центральной предельной теоремой, подчиняются нормальному распределению. Если член, который содержит ошибку, таков, что u оказывается суммой ошибок от нескольких причин, то независимо от того как могут быть распределены отдельные ошибки, их сумка u будет иметь нормальное распределение.
Если все перечислены условия соблюдены, то данная модель называется нормальной линейной регрессионной.
(Classical Normal linear regression model).
Условие независимости дисперсии ошибки от номера наблюдения  называется гомоскедастичностью (homoscedasticity).
называется гомоскедастичностью (homoscedasticity).
|
|
|
Случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью (heteroscedasticity).
 |

случай гомоскедастичности случай гетероскедастич-
ошибок ности ошибок
Условие  указывает на некоррелированность ошибок для разных наблюдений. Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда это условие не выполняется, говорят об автокорреляции остатков (serial correlation).
указывает на некоррелированность ошибок для разных наблюдений. Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда это условие не выполняется, говорят об автокорреляции остатков (serial correlation).
 |  |
P>0 P<0
Для простого случая  типичный вид данных представлен на рисунках.
типичный вид данных представлен на рисунках.
3.4 Линейная регрессия: подбор прямой. Случай два переменных Х и В
Уравнение прямой может быть полезное во многих ситуациях для обобщения наблюдаемой зависимости одной переменной от другой.
Рассмотрим как такое уравнение можно получить методом наименьших квадратов.
Допустимо, что линия регрессии переменные В от переменной Х имеет вид 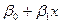 . Тогда линейная модель будет иметь вид
. Тогда линейная модель будет иметь вид
 , (1)
, (1)
u – остаточный фактор, возмущение.
В уравнении (1) величины  неизвестны, причем u в действительности трудно исследовать, поскольку она меняется от наблюдения к наблюдению
неизвестны, причем u в действительности трудно исследовать, поскольку она меняется от наблюдения к наблюдению 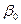 и
и 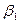 остаются постоянными, хоты мы не можем их находить не зная всех возможных значений Х и В, но мы можем оценить их, используя информацию, которая содержится в выборочных данных. Пусть и
остаются постоянными, хоты мы не можем их находить не зная всех возможных значений Х и В, но мы можем оценить их, используя информацию, которая содержится в выборочных данных. Пусть и  оценки параметров
оценки параметров 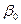 и
и 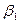 .
.
 , (2)
, (2)
в – предусмотрено значение В для данного Х. Уравнение (2) позволяет предусмотреть «действительное» среднее значение для заданного Х.
Процедурой оценивания будет метод наименьших квадратов (МНК).
При некоторых предположениях, какие мы рассмотрим позже, этот метод владеет определенными свойствами.
Пусть мы имеем множественное число из n наблюдений 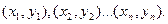
Тогда уравнение (1) можно записать в виде
 (3)
(3)
Сумма квадратов отклонений от действительной линии есть
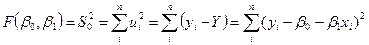 (4)
(4)
 Будем подбирать значения оценок
Будем подбирать значения оценок  и
и 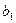 так, чтобы их постановка вместо
так, чтобы их постановка вместо  и
и 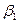 в уравнение (4) давала наименьшее возможное значение
в уравнение (4) давала наименьшее возможное значение  .
.
Линия, подобранная методом наименьших квадратов, такова, которая делает сумму квадратов всех этих вертикальных разногласий, указанных на рисунке, настолько малой насколько это возможно.
Дифференцируя уравнение (4) сначала по, потом по 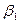 .
.
|
|
|
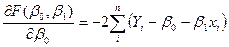
(5)
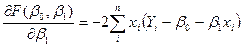
и приравнивая результаты к нулю, для оценок  и
и 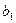 получим систему уравнений
получим систему уравнений
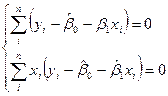 вместо
вместо 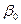 и
и 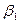 мы подставим
мы подставим 
 .
.
Решим эту систему относительно  и
и 
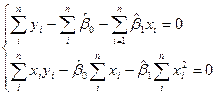 , (6)
, (6)




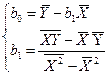 , (7)
, (7)
или
 , (8)
, (8)
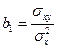 , (9)
, (9)
Действительно
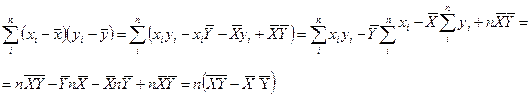 (10)
(10)
С помощью подстановки в уравнение 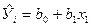 выражения для, можно получить оцениваемое уравнение регрессии
выражения для, можно получить оцениваемое уравнение регрессии 
Отметим, что поскольку, то 

(на практике из-за ошибок округления эта сумма может очутиться не точно ровной нулю).
В любом регрессионном задании сумма остатков всегда равна нулю, если член 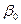 входит в модель. Это следствие первое из нормальных уравнений (6).
входит в модель. Это следствие первое из нормальных уравнений (6).
Исключение 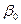 из модели приводит до того, что отзыв В обращается в нуль, когда все предикторы
из модели приводит до того, что отзыв В обращается в нуль, когда все предикторы 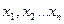 , уровни нулю.
, уровни нулю.
Такое предположение очень сильно. Исключение составляет линия регрессии, которая проходит через точку х=0, у=0 (отсекает нулевой отрезок).
Исключение 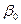 из модели всегда возможно с помощью “центрирования” данных, но это абсолютно не то же, что приравнять
из модели всегда возможно с помощью “центрирования” данных, но это абсолютно не то же, что приравнять 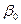 =0
=0
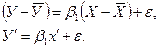
Попробуем построить выборочную линию регрессии для 25 пар наблюдений переменных Х и В, приведенных в таблицы, здесь же приведенные необходимые для последующего значения величины 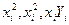 .
.
| Номер Опыту | В | Х | 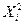
| 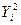
| ХУ |
| 10,98 | 35,3 | 1246,09 | 120,5604 | 387,594 | |
| 11,13 | 29,7 | 882,09 | 123,8769 | 330,561 | |
| 12,51 | 30,8 | 948,64 | 156,5001 | 385,308 | |
| 8,4 | 58,8 | 3457,44 | 70,56 | 493,92 | |
| 9,27 | 61,4 | 3769,96 | 85,9329 | 569,178 | |
| 8,73 | 71,3 | 5083,69 | 76,2129 | 622,449 | |
| 6,36 | 74,4 | 5535,36 | 40,4496 | 473,184 | |
| 8,5 | 76,7 | 5882,89 | 72,25 | 651,95 | |
| 7,82 | 70,7 | 4998,49 | 61,1524 | 552,874 | |
| 9,14 | 57,5 | 3306,25 | 83,5396 | 525,55 | |
| 8,24 | 46,4 | 2152,96 | 67,8976 | 382,336 | |
| 12,19 | 28,9 | 835,21 | 148,5961 | 352,291 | |
| 11,88 | 28,1 | 789,61 | 141,1344 | 333,828 | |
| 9,57 | 39,1 | 1528,81 | 91,5849 | 374,187 | |
| 10,94 | 46,8 | 2190,24 | 119,6836 | 511,992 | |
| 9,58 | 48,5 | 2352,25 | 91,7764 | 464,63 | |
| 10,09 | 59,3 | 3516,49 | 101,8081 | 598,337 | |
| 8,11 | 65,7721 | 567,7 | |||
| 6,83 | 46,6489 | 478,1 | |||
| 8,88 | 74,5 | 5550,25 | 78,8544 | 661,56 | |
| 7,68 | 72,1 | 5198,41 | 58,9824 | 553,728 | |
| 8,47 | 58,1 | 3375,61 | 71,7409 | 492,107 | |
| 8,86 | 44,6 | 1989,16 | 78,4996 | 395,156 | |
| 10,36 | 33,4 | 1115,56 | 107,3296 | 346,024 | |
| 11,08 | 28,6 | 817,96 | 122,7664 | 316,888 | |
| 235,6 | 76323,42 | 2284,11 | 11821,43 |
Приведены ниже величины получаем по очевидным формулам с целью вычислить коэффициенты b0 и b1.
|
|
|

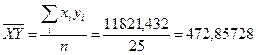

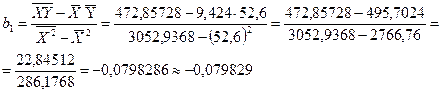
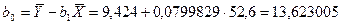
Окончательно для уравнения линейной регрессии получаем
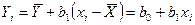 ,
,
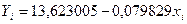 .
.
Построена линия регрессии нанесенная на рисунке вместе с диаграммой рассеяния.
 |
Рассмотрим вопрос, какая точность может быть приписана нашей оценке линии регрессии.
Рассмотрим следующую тождественность
|
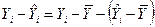 , (1)
, (1)

Геометрический смысл тождественности (1) легко понять из приведенного выше рисунка
Уравнение (1) можно переписать в виде  .
.
Возведем обе части этого уравнения в квадрат

Просуммируем это выражение от i=1 к n
 .
.
Окончательно
 , (2)
, (2)
Сумма квадратов относительно среднего = сумма квадратов относительно регрессии + сумма с обусловленной регрессией.
Введем обозначение

Ясно, что мы можем написать следующее равенство
 (3)
(3)
Не все действительные наблюдения лежат на прямой регрессии поскольку есть член 
 - дисперсия (разброс) обусловленный остаточными факторами. Пригодность линии регрессии для целей прогноза зависит от того, какая часть
- дисперсия (разброс) обусловленный остаточными факторами. Пригодность линии регрессии для целей прогноза зависит от того, какая часть 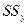 приходится на
приходится на 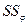 и
и  .
.
Мы будем довольны если 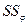 будет много больше, или, что тоже именно отношение
будет много больше, или, что тоже именно отношение
 , (4)
, (4)
не очень сильно отличается от единицы.
 - корреляционное отношение, коэффициент детерминирования.
- корреляционное отношение, коэффициент детерминирования.
Ясно, что имеет место формула
 , (5)
, (5)
Всякая сумма квадратов связана с числом, называемым ее степенями свободы. Это число показывает, как много независимых элементов инормации, что выходят из n независимых чисел  нужный для образования данной суммы квадратов.
нужный для образования данной суммы квадратов.
Для 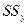 нужная n-1 степень свободы, поскольку
нужная n-1 степень свободы, поскольку 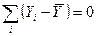 .
.
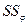 имеет одну степень свободы, поскольку
имеет одну степень свободы, поскольку 
 имеет n-2 степени свободы.
имеет n-2 степени свободы.
Это отображает тот факт, что даны остатки полученные для моделей прямой линии, которая требует оценивания двух параметров
n-1=1+n-2 (6)
Пользуясь уравнениями (2) и (6) мы можем построить таблицу дисперсионного анализа.
Таблица дисперсионного анализа
| Источник вариации | Число степенной свободы | Сумма квадратов SS | Средние квадраты MS |
| Обусловленный регрессией Относительно регрессии (остаток) | n-2 | 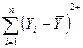 = = 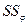
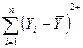 = = 
| 

|
| Общий, скорректированный на среднее | n-1 | 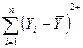 = = 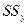
|
Средний квадрат относительно регрессии 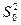 дает оценку, основанную на n-2 степенях свободы.
дает оценку, основанную на n-2 степенях свободы.
выполним вычисление для нашего примера
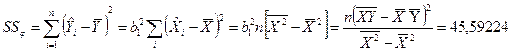


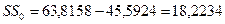
Таблица дисперсионного анализа
| Источник | Число степеней свободы | SS | MS |
| Регрессия Остаток | 45,5924 18,2234 | 45,5924

| |
| Общий, скорректированный | 63,8158 |
 - корреляционное отношение измеряет частицу общего разброса относительно среднего, такого, которое объясняет регрессией часто его выражают в процентах, умножая на 100.
- корреляционное отношение измеряет частицу общего разброса относительно среднего, такого, которое объясняет регрессией часто его выражают в процентах, умножая на 100.
 - коэффициент детерминирования
- коэффициент детерминирования
Таким образом получено уравнение регрессии,, на 71,44% объясняет общий разброс данных относительно среднего  .
.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 2492; Нарушение авторских прав?; Мы поможем в написании вашей работы!