
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Последовательное улучшение производственной программы
|
|
|
|
Линейная производственная задача
Задача о рациональном использовании производственных мощностей является одной из первых задач, для решения которой были применены методы линейного программирования. В общем виде математическая модель задачи об использовании производственных мощностей может быть получена следующим образом.
Предположим, что предприятие выпускает n видов изделий, имея m групп оборудования. Известны нормы времени на обработку каждого изделия на каждой группе оборудования, например, в минутах и фонд времени работы каждой группы оборудования. Требуется составить такой план производства, при котором прибыль предприятия будет наибольшей.
Примем следующие обозначения:
i – номер группы оборудования (I = 1,2, …, m);
j– номер вида изделия (j = 1,2, …, n);
aij – норма времени на обработку единицы j-го изделия на i-ой группе оборудования;
bi – действительный фонд времени работы i -й группы оборудования;
x j – планируемое количество единиц j -го изделия;
(x1, x2, …, xn) – искомый план производства.
Каков бы ни был план производства (x1, x2, …, xn), его компоненты должны удовлетворять условию, что суммарное время обработки всех изделий на данной группе оборудования не должно превышать фонда времени работы этой группы оборудования. На обработку x1 единиц первого изделия на i-й группе оборудования будет затрачено ai1x1 единиц времени, на обработку x2 единиц второго изделия на той же группе оборудования будет затрачено ai2x2 единиц времени и т.д. Необходимое время на обработку всех x1, x2, …, xnизделий на i -й группе оборудования будет равно сумме
 .
.
 Эта сумма не может превышать фонд времени работы i -й группы оборудования, т.е. должна быть меньше или равно bi. Выписывая такие условия для всех m групп оборудования, получаем:
Эта сумма не может превышать фонд времени работы i -й группы оборудования, т.е. должна быть меньше или равно bi. Выписывая такие условия для всех m групп оборудования, получаем:
|
|
|
a11x1 + a12x2 + … + a1nxn ≤ b1;
a21x1 + a22x2 + … + a2nxn ≤ b2; (1)
…………………………………………..
am1x1 + am2x2 + … + amnxn ≤ bm.
Так как компоненты плана суть количество изделий и, следовательно, не могут быть выражены отрицательными числами, то естественным образом добавляются условия:
x1 ³ 0, x 2³ 0 …, xn³ 0. (2)
Обозначим через с j прибыль на единицу j-го изделия.
При плане производства Х= (х1, х2, …, хn) прибыль предприятия будет равна:
P(Х) = c1x1 + c2x2 + … + cnxn. (3)
Мы хотим составить производственную программу X так, чтобы функция (3) приняла наибольшее значение при выполнении всех других условий.
Система линейных неравенств (1), (2) и линейная форма (3) образуют математическую модель задачи о рациональном использовании производственных мощностей. Среди всех решений системы линейных неравенств (1), удовлетворяющих условию неотрицательности (2), необходимо найти такое решение, при котором линейная форма (3) принимает наибольшее возможное значение. Это – задача линейного программирования.
Исходные параметры задачи могут быть представлены в виде технологической матрицы A затрат ресурсов на единицу продукции каждого вида, вектора B объемов ресурсов и вектора C удельной прибыли:

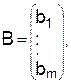 C=(c1, …, cn ).
C=(c1, …, cn ). 
В качестве примера рассмотрим задачу оптимизации производственной программы цеха, который может выпускать два вида изделий, имея четыре группы производственного оборудования. Пусть
 ,
, 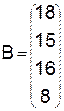 ,
,  , или кратко
, или кратко 
Задача состоит в том, чтобы найти производственную программу, максимизирующую прибыль:
 ; (4) при условиях:
; (4) при условиях:
 2x1 + 6x2 ≤ 18,
2x1 + 6x2 ≤ 18,
3x1 + 3x2 ≤ 15,
4x1 ≤ 16, (5)
x1 + 2x2 ≤ 8,
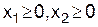 . (6)
. (6)
Полученную задачу линейного программирования с двумя переменными можно решить графически.
Напомним, что графический метод решения состоит из следующих этапов:
1. рисуем область допустимых решений, проводя соответствующие граничные прямые и выбирая соответствующие полуплоскости;
|
|
|
2. строим вектор-градиент целевой функции;
3. проводим линию уровня, перпендикулярную вектору-градиенту, которая проходит через область допустимых решений;
4. сдвигаем эту линию уровня параллельно самой себе в направлении вектора-градиента при решении задач на максимум (в направлении антиградиента при решении задач на минимум) до тех пор, пока она не станет опорной к области допустимых решений. Напомним, что прямая называется опорной к области допустимых решений, если выполняются следующие условия:
а. вся область допустимых решений находится по одну сторону от этой прямой;
б. эта прямая имеет хотя бы одну общую точку с областью допустимых решений;
5. оптимальным решением задачи являются точки пересечения опорной прямой с областью допустимых решений.
 Система линейных неравенств (5) и (6) определяет выпуклый многоугольник OLQRS допустимых решений. Линии уровня функции P перпендикулярны вектору-градиенту grad P = (6,9) и образуют семейство параллельных прямых (градиент указывает направление наиболее быстрого роста целевой функции). Наибольшего значения функция P достигает в точке Q. Координаты этой точки являются решением следующей системы: 3x1+3x2=15,
Система линейных неравенств (5) и (6) определяет выпуклый многоугольник OLQRS допустимых решений. Линии уровня функции P перпендикулярны вектору-градиенту grad P = (6,9) и образуют семейство параллельных прямых (градиент указывает направление наиболее быстрого роста целевой функции). Наибольшего значения функция P достигает в точке Q. Координаты этой точки являются решением следующей системы: 3x1+3x2=15,
2x1+6x2=18,
определяют оптимальный план производства x1=3, x2=2, а максимальная прибыль будет Pmax= 6·3+9·2=36. Графическое решение этой задачи представлено на рисунке 1.

Рис.1
Предположим теперь, что предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известна технологическая матрица А затрат любого ресурса на единицу каждого вида продукции, вектор В объемов ресурсов и вектор С удельной прибыли
 (7)
(7)
Требуется составить производственную программу, обеспечивающую предприятию наибольшую прибыль при имеющихся ограниченных ресурсах.
Математическая модель задачи:
найти производственную программу
Х = (x1, x2, x3, x4);
максимизирующую прибыль
Р(Х) = 36х1 + 14х2 + 25х3 + 50х4 ® max; (8)
 при ограничениях по ресурсам:
при ограничениях по ресурсам:
4x1 + 3x2 + 4x3 + 5x4 ≤ 208; (9)
2x1 + 5x2 + + 2x4 ≤ 107;
3x1 + x2 + 2x3 + 5x4 ≤ 181,
где по смыслу задачи
x1 ³ 0, x2 ³ 0, x3 ³ 0, x4 ³ 0. (т.е. X ³ 0, где 0 = (0, 0, 0, 0)). (10) Получили задачу на условный экстремум. Для ее решения систему неравенств (9) при помощи дополнительных неотрицательных неизвестных х5, х6, х7 заменим системой линейных алгебраических уравнений
|
|
|
 4x1 + 3x2 + 4x3 + 5x4 + x5 = 208; (11)
4x1 + 3x2 + 4x3 + 5x4 + x5 = 208; (11)
2x1 + 5x2 + + 2x4 + x6 = 107;
3x1 + x2 + 2x3 + 5x4 +x7 = 181,
где дополнительные переменные имеют смысл остатков соответствующих ресурсов. Среди всех решений системы уравнений (11), удовлетворяющих условию неотрицательности
х1 ³ 0, х2 ³ 0, …, х5 ³ 0, …, х7 ³ 0. (12)
надо найти то решение, при котором функция (8) примет наибольшее значение.
x1=0, x2=0, x3=0, x4=0, x5=208, x6=107, x7=181, (13)
первые четыре компоненты которого определяют производственную программу
x1=0, x2=0, x3=0, x4=0, (14)
по которой мы пока ничего не производим.
Из выражения (8) видно, что наиболее выгодно начинать производить продукцию четвертого вида, так как прибыль на единицу продукции здесь наибольшая. Чем больше выпуск этой продукции, тем больше прибыль. Выясним, до каких пор наши ресурсы позволяют увеличить выпуск этой продукции. Для этого придется записать для системы уравнений (11) общее решение
 x5 = 208 - 4x1 - 3x2 - 4x3 - 5x4; (15) x6 = 107 - 2x1 - 5x2 - 2x4;
x5 = 208 - 4x1 - 3x2 - 4x3 - 5x4; (15) x6 = 107 - 2x1 - 5x2 - 2x4;
x7 = 181 - 3x1 - x2 - 2x3 - 5x4.

 Мы пока сохраняем в общем решении х1=х2=х3=0 и увеличиваем только х4. При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств
Мы пока сохраняем в общем решении х1=х2=х3=0 и увеличиваем только х4. При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств
208 - 5x4 ≥ 0, х4 £ 208 /5,
107 - 2x4 ≥ 0, или х4 £ 107 /2, т.е. 0 £ х4 £  .
.
181 - 5x4 ≥ 0 х4 £ 181 /5,
Дадим х4 наибольшее значение х4 =181/5, которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (15). Получаем для системы уравнений (11) частное неотрицательное решение
х1=0, х2=0, х3=0, х4=  ; x5=27; x6=
; x5=27; x6=  ; x7=0. (16)
; x7=0. (16)
Нетрудно убедиться, что это решение является новым базисным неотрицательным решением системы линейных алгебраических уравнений (11), для получения которого достаточно было принять в системе (11) неизвестную х4 за разрешающую и перейти к новому предпочитаемому виду этой системы, сохранив правые части уравнений неотрицательными, для чего за разрешающее уравнение мы обязаны принять третье, так как
|
|
|
 ,
,
а34=5 будем называть разрешающим элементом. Совершим шаг Гаусса-Жордана, и применив известные формулы исключения, получаем для системы уравнений (11) новый предпочитаемый эквивалент
 x1 + 2x2 + 2x3 + x5 - x7 = 27;
x1 + 2x2 + 2x3 + x5 - x7 = 27;
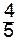 x1 +
x1 +  x2 -
x2 - 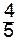 x3 + x6 -
x3 + x6 -  x7 =
x7 =  ; (17)
; (17)
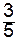 x1 +
x1 +  x2 +
x2 +  x3 + x4 +
x3 + x4 +  x7 =
x7 =  .
.
Приравняв к нулю свободные переменные х1, х2, х3, х7, получаем базисное неотрицательное решение, совпадающее с (16), причем первые четыре компоненты его определяют новую производственную программу
х1=0, х2=0, х3=0, х4=  . (18)
. (18)
Исследуем, является ли эта программа наилучшей, т.е. обеспечивает ли она наибольшую прибыль. Для этого выразим функцию прибыли (8) через новые свободные переменные х1, х2, х3, х7.
Из последнего уравнения системы (17) выражаем базисную переменную х4 через свободные и подставляем в (8). Получаем

 . (19)
. (19)
Видим, что программа (18) не является наилучшей, так как прибыль будет расти, если мы начнем производить или первую, или вторую, или третью продукцию, но наиболее быстро функция Р растет при возрастании х1. Поэтому принимаем х1 в системе (17) за разрешающую неизвестную, находим разрешающее уравнение по
 , (20) и исключаем х1 из всех уравнений системы (17), кроме первого уравнения. Получим следующий предпочитаемый эквивалент системы условий, который определит для системы (11) новое базисное неотрицательное решение и уже третью производственную программу, для исследования которого нам придется выразить функцию (19) через новые свободные переменные, удалив оттуда переменную х1, ставшую базисной. Мы видели выше, как это делается (удаляли х4 из (8)).
, (20) и исключаем х1 из всех уравнений системы (17), кроме первого уравнения. Получим следующий предпочитаемый эквивалент системы условий, который определит для системы (11) новое базисное неотрицательное решение и уже третью производственную программу, для исследования которого нам придется выразить функцию (19) через новые свободные переменные, удалив оттуда переменную х1, ставшую базисной. Мы видели выше, как это делается (удаляли х4 из (8)).
Важно обратить внимание на то, что эти удаления можно выполнить очень просто. Представим соотношение (8) в виде уравнения
-36х1 - 14х2 - 25х3 - 50х4 = 0 – P, (21)
и припишем его к системе (11). Получается вспомогательная система уравнений

4x1 + 3x2 + 4x3 + 5x4 + x5 = 208; (22) 2x1 + 5x2 + + 2x4 + x6 = 107;
3x1 + x2 + 2x3 + 5x4 +x7 = 181;
-36x1 - 14x2 - 25x3 - 50x4 = 0 – Р.
Напомним, что разрешающую неизвестную в системе (11) мы выбрали х4. Этой переменной в последнем уравнении системы (22) отвечает наименьший отрицательный коэффициент D4=-50. Затем мы нашли разрешающий элемент а34=5 и исключили неизвестную х4 из всех уравнений системы (11), кроме третьего. Далее нам пришлось х4 исключать и из функции (8). Теперь это можно сделать очень просто, если посмотреть на систему уравнений (22). Очевидно, достаточно умножить третье уравнение системы (22) на 10 и прибавить к четвертому; получим
-6х1 - 4х2 - 5х3 + 10х7 = 1810 – P. (23)
 Таким образом, мы преобразовали вспомогательную систему уравнений (22) к виду
Таким образом, мы преобразовали вспомогательную систему уравнений (22) к виду
x1 + 2x2 + 2x3 + x5 - x7 = 27;
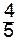 x1 +
x1 +  x2 -
x2 - 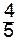 x3 + x6 -
x3 + x6 -  x7 =
x7 =  ; (24)
; (24)
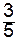 x1 +
x1 +  x2 +
x2 +  x3 + x4 +
x3 + x4 +  x7 =
x7 =  ;
;
-6x1 - 4x2 - 5x3 + 10x7 = 1810 – P.
Первые три уравнения этой системы представляют некоторый предпочитаемый эквивалент (17) системы уравнений (11) и определяют базисное неотрицательное решение (16) и соответственно производственную программу (18), а из последнего уравнения системы (24) получается выражение (19) функции цели через свободные переменные. Очевидно, если имеется хотя бы один отрицательный коэффициент Dj при какой-нибудь переменной xj в последнем уравнении системы (24), то производственная программа не является наилучшей и можно далее продолжать процесс ее улучшения. С помощью (19) мы выяснили, что следует начинать производить продукцию первого вида, т.е. фактически мы нашли в последнем уравнении системы (24) наименьший отрицательный коэффициент
min(Dj<0) = min(-6, -4, -5) = -6 = D1
и решили перевести свободную переменную х1 в число базисных, для чего, согласно (20) определили разрешающее уравнение и указали разрешающий элемент а11=1.
Учитывая сказанное выше, теперь мы будем преобразовывать не систему (17), а всю вспомогательную систему (24), по формулам исключения. Эта система преобразуется к виду
 x1 + 2x2 + 2x3 + x5 - x7 = 27;
x1 + 2x2 + 2x3 + x5 - x7 = 27;
3x2 - 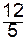 x3 -
x3 - 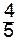 x5 + x6 +
x5 + x6 +  x7 = 13; (25)
x7 = 13; (25)
- x2 - 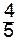 x3 + x4 -
x3 + x4 - 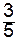 x5 +
x5 + 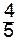 x7 = 20;
x7 = 20;
8x2 + 7x3 + 6x5 + 4x7 = 1972 – Р.
Первые три уравнения системы (25) представляют некоторый предпочитаемый эквивалент системы уравнений (11) и определяют базисное неотрицательное решение системы условий рассматриваемой задачи
x1=27, x2=0, x3=0, x4=20, x5=0, x6=13, x7=0, (26)
т.е. определяют производственную программу
x1=27, x2=0, x3=0, x4=20, (27)
и остатки ресурсов:
первого вида х5=0,
второго вида х6=13, (28)
третьего вида х7=0.
В последнем уравнении системы (25) среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели Р через остальные свободные переменные
Р = 1972 - 8х2 - 7х3 - 6х5 - 4х7, (29)
то становится совершенно очевидным (в силу того, что все xj ³ 0), что прибыль будет наибольшей тогда, когда
x2=0, x3=0, x5=0, x7=0. (30)
Это означает, что производственная программа (27) является наилучшей и обеспечивает предприятию наибольшую прибыль, т.о. ответ имеет вид:
X опт = (27, 0, 0, 20, (0, 13, 0)) и Р max = 1972. (31)
Итак, организовав направленный перебор базисных неотрицательных решений системы условий задачи, мы пришли к оптимальной производственной программе и нашли остатки ресурсов, а также максимальную прибыль.
Остается заметить, что процесс решения обычно записывается в виде так называемых симплексных таблиц,
| Б | 36 14 25 50 0 0 0 | α | β | Пояснения | ||
| СБ | (Базис) | Н | x1 x2 x3 x4 x5 x6 x7 | |||
 0 0
| х5 | 4 3 4 5 1 0 0 | 208/5 | P0 = CБ H | ||
| х6 | 2 5 0 2 0 1 0 | 107/2 | 2/5 |  
| ||
| х7 | 3 1 2 5 0 0 1 | 181/5 | - |  0 0
| ||
| P | -36 -14 -25 -50 0 0 0 | - | -10 | 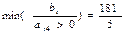
| ||
 0 0
| х5 | 1 2 2 0 1 0 -1 | - | 
| ||
| х6 | 173/5 | 4/5 23/5 -4/5 0 0 1 -2/5 | 173/4 | 4/5 | ||
| х4 | 181/5 | 3/5 1/5 2/5 1 0 0 1/5 | 181/3 | 3/5 | 
| |
| P | -6 -4 -5 0 0 0 10 | - | -6 | 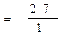
| ||
| х1 | 1 2 2 0 1 0 -1 | |||||
| х6 | 0 3 -12/5 0 -4/5 1 2/5 | все Dj ³ 0 | ||||
| х4 | 0 -1 -4/5 1 -3/5 0 4/5 | Здесь  – столбик коэффициентов при XБ; а – столбик коэффициентов при XБ; а  – столбик коэффициентов при Хj – столбик коэффициентов при Хj
| ||||
| P |  0 8 7 0 6 0 4 0 8 7 0 6 0 4
|

где представлены расширенные матрицы вспомогательных систем уравнений
(22) ® (24) ® (25).
Следует обратить внимание на экономический смысл элементов симплексных таблиц.
Значение дополнительной переменной в оптимальном плане показывает величину неиспользованного ресурса соответствующего вида.
Двойственная оценка фактической переменной показывает, насколько уменьшится значение целевой функции, если ввести в план одно изделие соответствующего вида.
Двойственная оценка дополнительной переменной показывает, насколько уменьшится целевая функция (прибыль) при уменьшении величины соответствующего ресурса на единицу (или увеличится при его увеличении).
Значение каждого коэффициента внутренних столбцов симплексной таблицы показывает, насколько уменьшится значение соответствующей базисной переменной, если ввести в план одно изделие, соответствующее свободной переменной; наименование базисной переменной указано в той строке, в которой расположен данный элемент, а свободной – в столбце.
Например, коэффициент D3=7 при переменной х3 показывает, что если произвести одну единицу продукции третьего вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 7 единиц.
В заключение заметим, что в рассматриваемом простейшем примере линейной производственной задачи возможна самопроверка результата.
Воспользуемся тем, что в оптимальной производственной программе x2=0, x3=0. Предположим, что вторую и третью продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию, и, решив эту задачу графически, убедимся в правильности решения симплексным методом.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!