Матричная модель производственной

ДИНАМИЧЕСКАЯ ЗАДАЧА УПРАВЛЕНИЯ ПРОИЗВОДСТВОМ И ЗАПАСАМИ

Динамическая задача управления производством и запасами формулируется следующим образом. Предприятие производит некоторое изделие, на которое оно имеет заказ на несколько (n) месяцев. Размеры заказов на каждый (j-й) месяц заданы (d_j) и могут изменяться от месяца к месяцу. Предприятие может в каждом месяце производить изделия и хранить их для удовлетворения будущих заказов. Затраты на производство изделия (x_j) и хранение запасов (y_j) в каждом месяце заданы. Требуется составить такой план производства изделий (x_j) и их запасов (y_j) на n месяцев, чтобы суммарные затраты на производство и хранение изделий были минимальны. Будем считать, что изделия (x_j) их запасы (y_j) и размеры заказов (d_j) принимают целые неотрицательные значения. Введем следующие обозначения:

x_j – число изделий, производимых в j – м месяце,

y_j – величина запаса к началу j – го месяца (это число не содержит изделий, производимых в j – м месяце),

d_j – заказ на изделия в j – м месяце,

f_j(x_j, y_j+1) – затраты на хранение и производство изделий в j – м месяце,

Будем считать, что величина запасов к началу первого месяца y₁ задана, а к концу последнего y_n+1=0.

Задача состоит в том, чтобы найти планы производства (x₁, x₂, …, x_n) и хранения запасов (y₂, y₃, …, y_n), компоненты которых удовлетворяют условиям материального баланса

x_j + y_j – d_j = y_j+1, j=1,2, …, n (1)

и минимизируют суммарные затраты на весь планируемый период

R= (2)

причем по смыслу задачи

х_j ³ 0, y_j ³ 0, j=1,2, …, n. (3)

Если целевая функция задачи (2) нелинейна, то задача (1) – (3) представляет собой задачу нелинейного программирования. Следует заметить, что затраты на производство изделий, как правило, имеют нелинейный характер, связанный с трудовыми, материальными, энергетическими и другими ресурсами.

Из условия y_n+1 =0 следует, что величина y_j+1 запаса к концу каждого месяца должна удовлетворять ограничениям

, j=1,2, …, n; (4)

т.е. запас к концу каждого месяца может обеспечить все заказы на оставшиеся до конца месяцы, но в последнем месяце y_n+1 =0. Кроме того, из соотношений (1) и (3) следует, что переменные x_j должны удовлетворять ограничениям

, j=1,2, …, n. (5) Напомним также, что переменные x_j, y_j и величины заказов d_j могут принимать целые неотрицательные значения.

Решение задачи (1) – (5) осуществим методом динамического программирования.

За параметр состояния s, характеризующий решение в каждом месяце, примем запас в конце k – го месяца

s=y_k+1, (6) а функцию состояния F_k(s) определим как минимальные затраты за первые k месяцев при выполнении условия (4)

, (7)

где минимум берется по неотрицательным целым значениям x₁, …, x_k, удовлетворяющим условиям

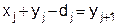, j = 1, …, k – 1; (8)

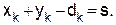(9)

Учитывая, что

(10)

и, так как величина запаса y_k к концу (k-1) периода, как видно из уравнения (9), равна

y_k= s + d_k – x_k, (11)

то мы приходим к рекуррентному соотношению

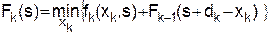, (12)

где минимум берется по единственной переменной x_k, которая согласно (5) может изменяться в пределах

, (13)

принимая целые значения, причем верхняя граница зависит от параметра состояния, изменяющегося в пределах

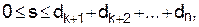(14)

а индекс k может принимать значения

k=2, 3, …, n (15)

Если k=1, то

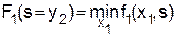, (16) где

x₁=s + d₁ – y_1, (17) 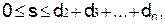(18)

т.е. на начальном этапе при заданном значении y₁ исходного запаса каждому значению параметра s отвечает только одно значение переменной x₁.

Применив известную вычислительную процедуру динамического программирования, на последнем шаге (при k=n) находим значения последних компонентов x_n^*, y_n^* оптимального решения, а остальные компоненты x_k^*, y_k^* определяем из условий баланса, двигаясь к началу (k=n-1,n-2, …, 1) в соответствии с результатами вычислений рекуррентного соотношения (12).

Рассмотрим более подробно функции затрат f_j(x_j, y_j+1) и рекуррентное соотношение. Пусть затраты 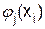на производство (закупку) x_j единиц изделия на этапе j имеют следующий вид:

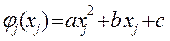^. (19)

Затраты на хранение запаса y_j+1, переходящего из этапа j в этап j+1

h_jy_j+1, (20)

где h_j – затраты на хранение единицы запаса на этапе j. Тогда затраты на производство и хранение на этапе j равны

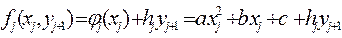^. (21)

Рекуррентное отношение (12) в этом случае принимает вид:

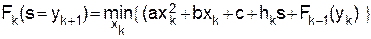, (22)

при условиях (11), (13) – (15). Если k=1, то 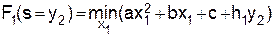, (23)

при условиях (17), (18).

Для дальнейших вычислений выражение в фигурных скобках (22) удобно представлять в виде суммы трех слагаемых:

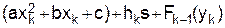. (24)

Пример. Рассмотрим задачу для трех месяцев (n=3). Пусть заказ на изделия на каждый месяц имеет соответственно следующие значения: d₁=3, d₂=2, d₃=4. В конце третьего месяца запас на изделия должен быть равен нулю, т.е. y₄=0. К началу первого месяца на складе имеется 2 изделия, т.е. y₁=2. Затраты на хранение единицы изделия для каждого месяца составляют соответственно h₁=1, h₂=3,h₃=2. Затраты на производство x_j изделий в каждом месяце 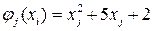. Требуется определить, сколько единиц изделий в каждом месяце нужно производить и хранить (для удовлетворения заказов на последующие месяцы), чтобы затраты на производство и хранение изделий за все три месяца были наименьшими.

Исходные данные этого примера, как это сделано в Приложении 4, можно записать так:

d₁ d₂ d₃ a b c h₁ h₂ h₃ y₁

3 2 4 1 5 2 1 3 2 2

Используя рекуррентное отношение (22), (23), последовательно вычисляем F₁(s=y₂), F₂(s=y₃), F₃(s=y₄=0). Результаты вычислений представляем в виде таблиц.

Положим k=1. Согласно (17) и (18),

х₁ = s +1; 0 ≤ s ≤ 6; F₁ (s = y₂) = x₁² + 5x₁ + 2 +y₂.

Результаты вычисления F₁(s=y₂) представлены в таблице 1.

Таблица 1

s=y2
F1(s=y2)
x1

Переходим ко второму этапу. Полагая k=2, вычисляем значения функции F₂(s=y₃) с помощью соотношения (22)

.

Согласно (11), (13) и (14) при k=2 с учетом заданных значений исходных данных, имеем

0 ≤ x₂ ≤ 6; 0 ≤ s ≤ 4; y₂ = s + 2 + x

Результаты вычисления F₂(s=y₃) представлены в таблице 2, где с учетом ранее сказанного, каждое значение рекуррентного соотношения представлено в виде суммы трех слагаемых. Кроме значений рекуррентного соотношения, в таблицу включены оптимальные значения x₃^*(s) изделий и оптимальные значения рекуррентного соотношения F₂(s), соответствующие значению запаса s.

Таблица 2

х2   s								x2^*(s)	F2(s)
	2+0+28	8+0+17	16+0+8	-	-	-	-
	2+3+41	8+3+28	16+3+17	26+3+8	-	-	-
	2+6+56	8+6+41	16+6+28	26+6+17	38+6+8	-	-
	2+9+73	8+9+56	16+9+41	26+9+28	38+9+17	52+9+8	-
	2+12+92	8+12+73	16+12+56	26+12+41	38+12+28	52+12+17	68+12+8

Из таблицы видно удобство представления правой части рекуррентного соотношения в виде суммы трех слагаемых: значения первых слагаемых (значения затрат на производство изделий) одинаковы по столбцам таблицы (где заданы количества, производимых изделий), значения вторых слагаемых (значения затрат на хранение запасов) одинаковы по строкам таблицы (где заданы значения запасов), значения третьих слагаемых выбираются из таблицы 1 при соответствующих значениях производства изделий (x₂) и запасов (s), с помощью которых определяется значение y₂. Из таблицы 2 видно, что эти значения выбираются из таблицы 1 последовательно слева направо. При этом значения третьих слагаемых одинаковы для клеток таблицы, которые «параллельны северо-западной диагонали». Прочерки в таблице соответствуют запрещенным по условиям задачи значениям x₂. Следует также заметить, что в том случае, когда сумма в фигурных скобках рекуррентного соотношения принимает одинаковые значения при различных оптимальных значениях x₂^*(s), то все такие значениях x₂^*(s) должны были бы быть указаны в столбце x₂^*(s) таблицы 2. В этом случае решаемая задача может иметь множество оптимальных решений.

Переходим к последнему этапу (k=3). Поскольку на последнем этапе s=y₄=0 и из соотношения (11), (13) с учетом исходных данных 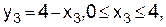то таблица для вычисления значений рекуррентного соотношения

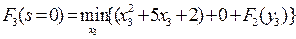
для этого этапа имеет вид, представленный в таблице 3.

Таблица 3

x3						x3^*	F3(0)
s=0	2+0+78	8+0+63	16+0+49	26+0+36	38+0+24	3; 4

Таким образом, минимум целевой функции затрат на производство изделий и хранение их запасов за три месяца равен 62 и достигается при двух значениях производства изделий в третьем месяце: x₃^*=3 и x₃^*=4, т.е. задача нашего примера имеет 2 решения (здесь произошел случай, указанный в предыдущем замечании).

Найдем эти решения, последовательно продвигаясь от последнего этапа (третьего месяца) к первому, пользуясь данными вычисления рекуррентных соотношений в таблицах 1-3 и условием баланса (11). При x₃^*=3 из (11) при значении k=3 с учетом исходных данных получаем: y₃*=4-3=1. Из таблицы 2 находим, что для y₃^*=1 (s=1) x₂^*=2. Из (11) при значении k=2 получаем: y₂^*=1+2-2=1. И, наконец, из таблицы 1 находим, что для y₁^*=1 x₁^* =2. По условию (11) y₁^*= y₂+d₁- x₁^* =1+3-2=2, что совпадает с исходным значением. Итак, первый оптимальный план производства и запасов имеет вид

x₁=2, y₁=2; x₂=2, y₂=1; x₃=3, y₃=1,

а минимальные общие затраты составляют 62 единицы.

Полезно проверить поученный результат. Для этого по исходным данным и найденному плану проверяем выполнение условий баланса (1) для каждого месяца. Для первого месяца находим x₁ + y₁ – d₁ = y₂, т.е. 2+2-3=1, для второго месяца x₂ + y₂ – d₂ = y₃, т.е. 2+1-2=1, для третьего месяца x₃ + y₃ – d₃ = y₄=0, т.е. 3+1-4=0. Важно проверить равенство j(x₁)+ j(x₂) +j(x₃) +h₁y₂+h₂y₃=F₃(y₄=0),

16 + 16 + 26 + 1 + 3 = 62.

Из аналогичных соображений при x₃^* =4 последовательно находим y₃^*=0, x₂^* =2, y₂^*=0, x₁^* =1, y₁^*=2. В этом варианте предприятие не хранит запасов изделий. Таким образом, второй оптимальный план производства и запасов имеет вид

x₁=1, y₁=2; x₂=2, y₂=0; x₃=2, y₃=0,

при том же значении минимальных затрат 62 единицы.

Дата добавления: 2015-06-04