Средняя квадратическая и средняя кубическая

Средняя геометрическая

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая простая исчисляется извлечением корня степени и из произведений отдельных значений — вариантов признака х:

где n — число вариантов; П — знак произведения.

Средняя геометрическая взвешенная исчисляется:

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая (например, для вычисления средней величины стороны и квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны и кубов).

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

где 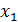, ,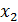… 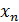- значения признака, n- их число.

Средняя квадратическая взвешенная:

,

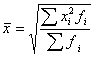где 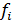- веса.

Средняя кубическая простая является кубическим корнем из частного от деления суммы кубов отдельных значений признака на их число:

,

где 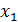, ,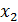… 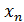- значения признака, n- их число.

Средняя кубическая взвешенная:

,

где 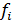- веса.

Средняя квадратическая и средняя кубическая необходимы для расчета средних значений, когда исходные данные представлены в квадратных или кубических единицах измерения.

Структурные средние

Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).

В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.

Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:

,

где 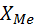- нижняя граница интервала, который содержит медиану;

– величина медианного интервала;

– частота медианного интервала;

- сумма накопленных частот интервалов, предшествующих медианному;

– сумма частот интервалов, предшествующих медианному.

Пример. Предположим, что в одной комнате оказалось 19 бедняков и один миллиардер. Каждый кладет на стол деньги из своего кармана. По пять долларов кладет каждый бедняк, а миллиардер — $1 млрд. В сумме получается $1 000 000 095. Если мы разделим деньги равными долями на 20 человек, то получим $50 000 004,75. Это будет среднее арифметическое значение суммы наличных, которая была у всех 20 человек в этой комнате.

Медиана в этом случае будет равна $5 (полусумма десятого и одиннадцатого, срединных значений ранжированного ряда). Можно интерпретировать это следующим образом. Разделив нашу компанию на две равные группы по 10 человек, мы можем утверждать, что в первой группе каждый положил на стол не больше $5, во второй же не меньше $5. В общем случае можно сказать, что медиана это то, сколько принес с собой средний человек. Наоборот, среднее арифметическое же совершенно неподходящая характеристика в нашем случае, поскольку выходит, что каждый, будь то бедняк или миллиардер, имел приблизительно $50 000 004,75.

Кумулята предназначена для графического изображения накопленных частот (частостей) количественных данных. При построении кумуляты по оси абсцисс откладываются варианты ряда (верхняя граница интервала, в данном примере – возраст в годах), а по оси ординат накопленные частоты (частости). Из точки на шкале накопленных частот (частостей), соответствующей 50% (или порядковому номеру медианы), параллельно оси абсцисс, до пересечения с кумулятой, проводится прямая. Затем из точки пересечения данной прямой с кумулятой на ось абсцисс опускается перпендикуляр. Точка пересечения прямой с осью абсцисс и является медианой.

Рассмотрим определение медианы по данным о распределении населения Российской Федерации по полу и возрастным группам на начало 2007 года (Таблица 1. 2.5).

Пример. Все население России на начало 2007 года составляло 142 221 млн. человек, из них мужчины – 65 849 млн. человек, женщины - 76372 млн. человек.

В Таблице 1.2.5 население разбито на 15 возрастных групп. Ширина каждого интервала равна четырем годам. Следует отметить, что у последней группы открытый интервал, а у остальных групп –закрытый.

Таблица 1.2.5

Распределение населения Российской Федерации по полу и возрастным группам на начало 2007 года (тыс. чел.)

Возраст, лет	Все население
Все население	мужчины и женщины	мужчины	женщины
в том числе в возрасте, лет:
0-4
5-9
10-14
15-19
20-24
25-29
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
70 и более

Построим кумулятивную кривую. Левая ось (ось ординат) показывает накопленные частости, нижняя ось (ось абсцисс) – количество лет. От оси ординат, из точки соответствующей 50%, параллельно оси абсцисс проводится прямая до пересечения ее с кумулятой. Из точки пересечения прямой и кумуляты, на ось абсцисс опускается перпендикуляр (рис. 1.2.1).

Рис. 1.2.1 - Расчет медианы по интервальному ряду распределения графическим способом (по частостям).

Пример. Определить медиану заработной платы рабочих.

Месячная з/п, руб.	Число рабочих	Сумма накопительных частот
		8 (2+6)
		24 (8+16)
		—
		—

Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составила ее половина - 20.

Накопленная сумма частот ряда получилась равной Варианта, соответствующая этой сумме, т.е. 160 руб., и есть медиана ряда.

Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.

Пример. Определить медиану заработной платы:

Месячная з/п, руб.	Число рабочих	Сумма накопительных частот
		8 (2+6)
		20 (8+12)
		—
		—

Медиана будет равна:

Ме = (150 + 170) / 2 = 160 руб.

Рассмотрим расчет медианы в интервальном вариационном ряду.

Пример. Определить медиану числа рабочих:

Группы предприятий по числу рабочих	Число предприятий	Сумма накопительных частот
100 — 200
200 — 300		4 (1+3)
300 — 400		11 (4+7)
400 — 500		41 (11+30)
500 — 600		—
600 — 700		—
700 — 800		—
ИТОГО

Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений, соответствует интервалу 400 - 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.

Известно, что:

Следовательно,

.

Мода – варианта, чаще всего встречающаяся в ряду распределения, т.е. варианта, которой соответствует наибольшая частота.

Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой расположена наибольшая частота, и будет модой.

В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Вычисление моды производится по следующей формуле:

, где

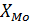– начло (нижняя граница) модального интервала;

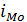– величина интервала;

– частота модального интервала;

– частота интервала, предшествующего модальному;

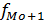– частота интервала, следующего за модальным.

Мода применяется, например, при определении размера одежда, обуви, пользующихся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар на рынке и т. д.

Пример. В таблице приведены итоговые оценки учащихся некоторого класса по математике. Найти моду данного распределения.

Количество баллов
Число учащихся

Из всех оценок чаще всего встречается 7 баллов: шесть раз. Поэтому Мо = 7. Этот результат имеет вполне определенный смысл - больше всего учащихся класса имеют по математике 7 баллов.

Пример. Распределение проданной обуви по размерам характеризуется следующими показателями:

размер обуви											и выше
число пар, в % к итогу	—										—

В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей.

Пример. Распределение предприятий по численности промышленно – производственного персонала характеризуется следующими данными:

Группы предприятий по числу работающих, чел.	Число предприятий
100-200
200-300
300-400
400-500
500-600
600-700
700-800

В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения.

Введем следующие обозначения:

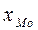=400, =100, =30, =7, =19

Подставим эти значения в формулу моды и произведем вычисления:

Квартили – это значения признака, делящие ранжированную совокупность на четыре равновеликие части.

Различают:

· нижнюю квартиль 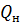, отделяющую ¼ часть совокупности с наименьшими значениями признака;

· среднюю квартиль – медиану;

· верхнюю квартиль 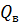, отделяющую ¼ часть совокупности с наибольшими значениями признака.

Для расчета квартилей по интервальному вариационному ряду используются формулы:

где

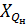- нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой, превышающей 25%);

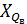- нижняя граница интервал, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой, превышающей 75%);

- накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;

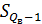- накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;

h – длина интервала;

, - частота интервала, содержащего нижний и верхний квартиль соответственно.

Квартильный размах – разница между верхней и нижней квартилями:

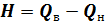
Квартильный размах охватывает 50 % значений выборки.

Пример. Для данных таблицы:

№ интервала	Интервалы	Середина интервала	Частота	Накопленная частота
Нижняя граница	Верхняя граница
	4,25	5,95	5,1
	5,95	7,65	6,8
	7,65	9,35	8,5
	9,35	11,05	10,2
	11,05	12,75	11,9
	12,75	14,45	13,6
	14,45	16,15	15,3
Всего:		-

Интервал, содержащий нижнюю квартиль – 3-ий, т. к. накопленная частота (27) первая превышает ¼ общей суммы частот (12,5).

Интервал, содержащий верхнюю квартиль – 5-ий, т. к. накопленная частота (42) первая превышает ¾ общей суммы частот (37,5).

,

Квартильный размах – полоса, шириной 11,48-7,81=3,67 содержит 50% значений выборки.

1.3 Правило мажорантности средних

Средние величины, применяемые в статистике, относятся к классу степенных средних. Общая формула степенной средней выглядит следующим образом:

,

где - степенная средняя;

x – меняющиеся величины признака (варианты);

n – число вариант;

m – показатель степени средней.

Изменение значения показателя степени средней (m) определяет вид средней величины:

· если m=1, получается средняя арифметическая;

· если m=2, получается средняя квадратическая;

· если m=3, получается средняя кубическая;

· если m= - 1, получается средняя гармоническая;

· если m=0, получается средняя геометрическая.

Чем больше показатель степени в формуле степенной средней, тем больше величина средней. Это правило называется правилом мажорантности средних.

1.4 Расчет средних по результатам группировки

Очень часто исходные данные для анализа бывают представлены в сгруппированном виде, когда для каждого значения осредняемого признака X сообщается частота его повторения.

В этих случаях средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических либо гармонических). Сложности возникают, когда в сгруппированных данных указывается не конкретное значение признака А по каждой группе, а лишь интервал его изменения. В данном случае правильный расчет общей средней величины возможен, если каким-либо способом удается получить среднее значение признака по каждой группе; далее используются обычные формулы средних взвешенных.

Если же средние значения признака в группах определить по имеющимся сведениям нельзя, то их заменяют серединами интервалов, получая в итоге некоторое, чаще всего вполне удовлетворительное, приближение к среднему значению.

Дата добавления: 2015-06-26