
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вариация
2.1 Понятие о вариации и задачи ее изучения
Вариация – различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени. [2, с. 50]
Статистический анализ вариации предполагает выполнение следующих основных этапов:
1) Построение вариационного ряда.
2) Графическое изображение вариационного ряда.
3) Расчет показателей центра распределения и структурных характеристик вариационного ряда.
4) Расчет показателей размера и интенсивности вариации.
5) Оценка вариационного ряда на асимметрию и эксцесс.
Построение вариационного ряда (ряда распределения) – это упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с тем или иным его значением.
Предположим, в результате обобщения итогов выборочного бюджетного обследования города N-ска построен вариационный ряд, отражающий распределение жителей города по величине среднедушевого дохода.
Таблица 2.1.1
| Среднедушевой денежный доход в среднем за месяц, тыс. руб. | Число жителей | Накопленные частоты (S) | Середина интервала (x) | xf | xw | |
| чел. (f) | в % к итогу (w) | |||||
| До 0.5 | 0,9 | 0,9 | 0,25 | 6,5 | 0,225 | |
| 0,5 – 1,0 | 16,5 | 17,4 | 0,75 | 347,25 | 12,375 | |
| 1,0 – 1,5 | 24,6 | 42,0 | 1,25 | 862,5 | 30,75 | |
| 1,5 – 2,0 | 18,8 | 60,8 | 1,75 | 924,0 | 32,9 | |
| 2,0 – 2,5 | 15,4 | 76,2 | 2,25 | 976,5 | 34,65 | |
| 2,5 – 3,0 | 12,5 | 88,7 | 2,75 | 962,5 | 34,375 | |
| 3,0 и более | 11,3 | 100,0 | 3,25 | 1033,5 | 36,725 | |
| Итого | 100,0 | - | - | 5112,75 | 182,0 |
В составе любого вариационного ряда можно выделить три основных элемента: варианты, частоты, частости.
Варианты – это значения, которые принимает исследуемый признак.
Если варианты представлены в виде целочисленных величин, вариационный ряд называют дискретным, если в виде интервалов – интервальным. В табл. 2.1.1 представлен интервальный вариационный ряд, вариантами которого являются значения среднедушевого денежного дохода населения (гр. 1).
Частоты вариационного ряда – абсолютная численность отдельных групп с различными значениями признака (гр. 2).
Частости вариационного ряда – удельные веса (доли) отдельных групп в общей численности совокупности (гр. 3).
При характеристике колеблемости признака применяют систему абсолютных и относительных показателей.
К абсолютным показателям вариации относятся:
1) размах вариации  ;
;
2) среднее линейное отклонение d;
3) дисперсия 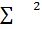 ;
;
4) среднеквадратическое отклонение  .
.
Эти показатели (кроме дисперсии) измеряются в тех же единицах, что и сам признак: в тоннах, метрах, секундах, рублях. К относительным показателям вариации относятся:
· коэффициент осцилляции 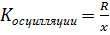 ;
;
· линейный коэффициент вариации 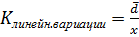 ;
;
· простой коэффициент вариации  .
.
Эти показатели выражаются в процентах или относительных величинах.
2.2 Графическое изображение вариационного ряда
Графическое изображение вариационных рядов облегчает их анализ и позволяет судить о форме распределения. Для графического изображения вариационного ряда в статистике строят гистограмму, полигон и кумуляту распределения.
 Гистограмма – столбиковая диаграмма, для построения которой на оси абсцисс откладывают отрезки, равные величине интервалов вариационного ряда. На отрезках строят прямоугольники, высота которых в принятом масштабе по оси ординат соответствует частотам (или частостям) (рис. 2.2.1).
Гистограмма – столбиковая диаграмма, для построения которой на оси абсцисс откладывают отрезки, равные величине интервалов вариационного ряда. На отрезках строят прямоугольники, высота которых в принятом масштабе по оси ординат соответствует частотам (или частостям) (рис. 2.2.1).
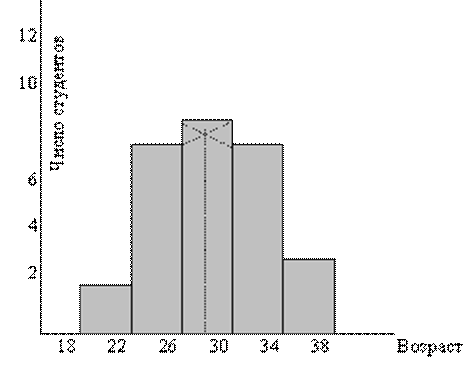
Рис. 2.2.1 Гистограмма распределения студентов по возрасту
Для графического изображения дискретного вариационного ряда применяют полигон распределения, для построения которого необходимо соединить прямыми отрезками точки с координатами x, w (рис. 2.2.2). Крайние точки полученного графика соединяют с точками по оси абсцисс, отстающими на одно деление в принятом масштабе от минимального и максимального значения вариант. Полигон может быть построен и для интервального вариационного ряда, для этого в качестве координат по оси абсцисс используют середины интервалов. Очевидно, что гистограмма легко может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить отрезками прямых, при этом середины верхних сторон двух крайних прямоугольников соединить с осью абсцисс в точках, отстоящих в принятом масштабе на величину интервалов от середины первого и последнего интервалов.

Рис. 2.2.2 Полигон распределения
Кумулята распределения строится по накопленным частотам (частостям). Накопленные частоты (частости) определяют последовательным суммированием частот (частостей), они показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое значение (гр. 4, табл. 2.1.1). При построении кумуляты интервального ряда (рис. 2.2.3) нижней границе первого интервала соответствует нулевая частота (частость), верхней – вся частота (частость) первого интервала. Верхней границе второго интервала – сумма частот (частостей) первого и второго интервалов и т. д. Верхней границе последнего интервала – сумма накопленных частот (частостей) во всех интервалах, что соответствует общей численности изучаемой совокупности на 100%.
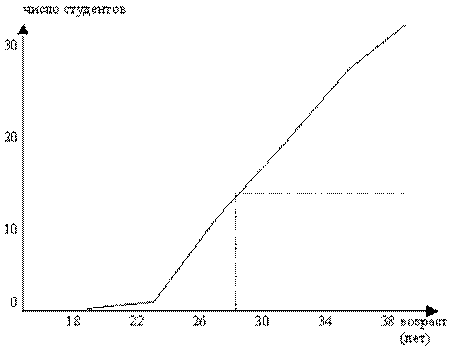
Рис. 2.2.3 Кумулята распределения студентов по возрасту
2.3 Показатели центра распределения и структурные характеристики вариационного ряда
Для характеристики среднего значения признака в вариационном ряду используются так называемые показатели центра распределения. К ним относятся средняя величина признака, мода и медиана.
Расчет средней величины признака (х) в вариационном ряду осуществляется по формуле средней арифметической взвешенной:
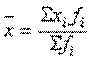
При расчете средней величины интервального ряда в качестве вариантов признака используются значения середины интервалов (гр. 5, табл. 2.1.1). Для нахождения середины открытых интервалов необходимо их предварительно условно закрыть, т. е. определить недостающую верхнюю и нижнюю границы. Принято считать, что в первой группе величина интервала равна интервалу второй группы, а в последней – интервалу предыдущей. В рассматриваемом примере используется ряд с равными интервалами, величина которых 0,5 тыс. руб. Тогда условная нижняя граница первого интервала будет равна:0,5 тыс. руб. – 0,5 тыс. руб. =0, а середина – 0,25 тыс. руб., условная верхняя граница последнего интервала: 3,0 тыс. руб. + 0,5 тыс. руб., а середина – 3,25 тыс. руб.
Осуществим расчет средней величины месячного среднедушевого денежного дохода (х), используя в качестве весов частоты распределения (f). Промежуточные расчеты запишем в гр. 6 табл. 2.1.1. Тогда
Х ср. = 5112,75/2809 =1,82 тыс. руб.
Месячный среднедушевой доход составляет 1820 руб.
Мода – значение признака, наиболее часто встречающееся в изучаемой совокупности. В дискретном ряду модой является вариант с наибольшей частотой (частостью). В интервальном вариационном ряду мода рассчитывается по формуле:

Модальный интервал – это интервал, имеющий наибольшую частоту (частость). В нашем примере это третий интервал от 1,0 до 1,5 тыс. руб.
Рассчитаем модальное значение признака, используя в качестве весов частости распределения:
Мо =  =1,29 тыс. руб.
=1,29 тыс. руб.
Таким образом в нашем примере наиболее часто встречающаяся величина среднедушевого дохода составляет 1290 руб.
Отметим, что вычисления моды в интервальном ряду является весьма условным.
Приближенно модальное значение признака можно определить и графически – по гистограмме. Для этого нужно взять столбец, имеющий наибольшую высоту, и из его левого верхнего угла провести отрезок в верхний угол последующего столбца, а из правого угла – в верхний правый угол предыдущего. Абсцисс точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности.
Медиана – вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части, таким образом, что половина единиц совокупности имеют значение признака меньше, чем медиана, а половина – больше, чем медиана. В интервальном ряду медиана определяется по формуле:

Медианный интервал – это интервал, в котором находится порядковый номер медианы. Для его определения необходимо подсчитать сумму накопленных частот (частостей) до числа, превышающего половину объема совокупности. По данным гр. 4 табл. 2.2.1 находим интервал, сумма накопленных частот в котором превышает 50%. Это интервал от 1,5 до 2,0 тыс. руб., он и является медианным. Тогда
Ме = 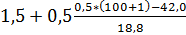 =1,72 тыс. руб.
=1,72 тыс. руб.
Медиану приближенно можно определить графически – по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения и является медианой.
Расчет модального и медианного значений для вариационных рядов с неравными интервалами осуществляется по формулам, аналогичным приведенным выше, только вместо показателей частот (частостей) используются показатели абсолютной или относительной плотности распределения, которые обеспечивают сопоставимость неравных интервалов. Показатели плотности распределения находятся как отношения частот (частостей) к величине интервала:
- абсолютная плотность распределения
 ;
;
- относительная плотность распределения
 , где i – величина интервала.
, где i – величина интервала.
По соотношению характеристик центра распределения (средней величины, моды и медианы) можно судить о симметричности эмпирического ряда распределения. Симметричным является распределение, в котором частоты двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. В симметричном распределение средняя величина, медиана и мода равны между собой:
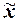 =Mo=Me.
=Mo=Me.
Если 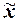 >Mo>Me, то имеет место правосторонняя асимметрия, т. е. большая часть единиц совокупности имеет значение изучаемого признака, превышающие модальное значение. На графике распределения правая ветвь относительно максимальной ординаты вытянута больше, чем левая.
>Mo>Me, то имеет место правосторонняя асимметрия, т. е. большая часть единиц совокупности имеет значение изучаемого признака, превышающие модальное значение. На графике распределения правая ветвь относительно максимальной ординаты вытянута больше, чем левая.
Соотношение 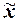 <Mo<Me характерно для левосторонней асимметрии, при которой большая часть единиц совокупности имеет значение признака ниже модального. На графике распределения левая ветвь вытянута больше, чем правая.
<Mo<Me характерно для левосторонней асимметрии, при которой большая часть единиц совокупности имеет значение признака ниже модального. На графике распределения левая ветвь вытянута больше, чем правая.
Нашему примеру соответствует соотношение 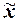 >Mo>Me (1820 руб. > 1290 руб.), характерное для правосторонней асимметрии. Наличие правосторонней асимметрии свидетельствует о том, что большая часть города имела месячный среднедушевой доход выше, чем его модальное значение (1290 руб.).
>Mo>Me (1820 руб. > 1290 руб.), характерное для правосторонней асимметрии. Наличие правосторонней асимметрии свидетельствует о том, что большая часть города имела месячный среднедушевой доход выше, чем его модальное значение (1290 руб.).
При анализе вариационного ряда важно знать не только направление асимметрии (правосторонняя или левосторонняя), но и ее степень, которая измеряется с помощью коэффициентов асимметрии.
Моду и медиану называют еще структурными средними, поскольку они дают количественную характеристику структуры строение вариационных рядов. К структурным характеристикам относятся и другие порядковые статистики: квартили – делящие ряд на 4 равные части, децили – делящие ряд на 10 частей, перцинтили – на 100 частей и др.
Общая схема расчета децилей следующая:
1) поскольку децили отсекают десятые части совокупности, по накопленным частостям определяем интервалы, куда попадают порядковые номера децилей: для первой децили – интервал, где находится вариант, отсекающий 10% совокупности с наименьшими значениями признака; для второй – 20% и т. д.; для девятой децили – интервал, содержащий вариант, отсекающий 90% с наименьшими значениями признака;
2) рассчитываем величину децилей по формулам, аналогичным формуле для нахождения медианы. Например, первая и девятая децили находятся по формулам:
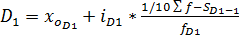 ;
;
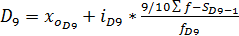 ,
,
где 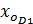 ,
,  - начала интервалов, где находятся первая и девятая децили;
- начала интервалов, где находятся первая и девятая децили;  ,
,  - величины интервалов, где находятся первая и девятая децили;
- величины интервалов, где находятся первая и девятая децили; 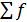 – общая сумма частот (частостей);
– общая сумма частот (частостей); 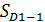 ,
, 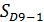 - суммы частот (частостей), накопленных в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили.
- суммы частот (частостей), накопленных в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили.
Для нашего примера первая дециль попадает в интервал от 0,5 до 1,0 тыс. руб. (сумма накопленных в этом интервале частостей составляет 17,4%, что превышает 10%), девятая дециль – в интервал от 3,0 тыс. руб. и более (в этом интервале находится 10% населения с наибольшими доходами). Найдем вершину соответствующих децилей.
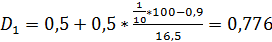 тыс. руб.
тыс. руб.
Следовательно, максимальная величина месячного среднедушевого дохода у 10% наименее обеспеченных жителей составляла 776 руб.
 тыс. руб.
тыс. руб.
Минимальная величина месячного среднедушевого дохода у 10% наиболее обеспеченного населения города составила 3058 руб.
Соотношение децильных доходов в социальной статистике получило название коэффициента децильной дифференциации доходов населения ( ):
):
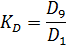
В рассматриваемом примере
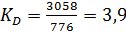 .
.
Это означает, что минимальный месячный среднедушевой доход 10% наиболее обеспеченного населения превышал максимальный доход 10% наименее обеспеченного населения в 3,9 раза.
2.4 Показатели размера и интенсивности вариации
2.5
Для характеристики размера вариации в статистике применяются абсолютные показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и дисперсия.
Размах вариации (размах колебаний) представляет собой разность между максимальным и минимальным значениями признака в совокупности:
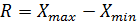
Величина R показывает, в каких пределах колеблется размер признака, образующего ряд распределения. Показатель R выражается в тех же единицах измерения, что и варианты ряда. Но размах вариации как показатель колеблемости имеет существенный недостаток. Его величина определяется двумя крайними значениями признака, в то время как колеблемость последнего в целом складывается из суммы всех его значений. Поэтому размах вариации может в ряде случаев неправильно характеризовать колеблемость признака. Если, например, на большой посевной площади с равномерной в целом урожайностью встречаются отдельные небольшие участки с исключительно высокой и низкой урожайностью, то размах вариации будет иметь значительный размер, хотя колеблемость урожайности в целом незначительна. Следовательно, размах вариации не отражает варьирования признака основной массы единиц совокупности.
Пример. Вычислить размах вариации:
Группы предприятий по объему товарооборота, млн.руб. 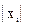
| Число предприятий 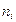
|
| 90 — 100 | |
| 100 — 110 | |
| 110 — 120 | |
| 120 — 130 | |
| ИТОГО |
Определяем показатель размаха вариации:
R = 130 - 90 = 40 млн. руб.
В связи с тем, что каждое индивидуальное значение признака отклоняется от средней на определенную величину, очевидно, что мерой вариации может служить средняя из отклонений каждой отдельной варианты от их средней. Такими показателями являются среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.
Среднее линейное отклонение представляет собой среднюю из абсолютных значений отклонений отдельных вариант от их средней. Так как алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю, т. е.  (второе свойство средней арифметической), при исчислении среднего линейного отклонения принимаются во внимание только абсолютные значения отклонения без учета знаков («+» или «-»). Среднее линейное отклонение рассчитывается по формуле средней арифметической простой:
(второе свойство средней арифметической), при исчислении среднего линейного отклонения принимаются во внимание только абсолютные значения отклонения без учета знаков («+» или «-»). Среднее линейное отклонение рассчитывается по формуле средней арифметической простой:
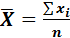 ,
,
или средней арифметической взвешенной:
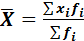 .
.
Пример. Вычислить среднее линейное отклонение:
| Табельный номер рабочего | 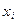
| 
| /  / /
|
| - 8 | |||
| - 7 | |||
| Итого |
X= 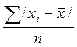 =
= 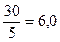
Средним квадратическим отклонением случайной величины называется корень квадратный из ее дисперсии:
Среднее квадратическое отклонение, равно корню квадратному из дисперсии. Оно может быть простым или взвешенным.
S (х i - х)
s = ------------------
n
или
S (х i - x) ¦ i
s = --------------------.
S ¦ i
Среднее квадратическое отклонение, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные варианты признака от среднего значения. Они выражаются в тех же единицах измерения, что и признак (в метрах, тоннах, рублях и т.д.).
Среднее квадратическое отклонение часто используется в качестве единицы измерения отклонений от средней арифметической. В зарубежной литературе этот показатель называется нормированным, или стандартизированным, отклонением.
По свойству мажорантности средних величин среднее квадратическое отклонение всегда больше среднего линейного отклонения. Если распределение признака близко к нормальному или симметричному распределению, то между s и d существует взаимосвязь: d = 0,8s или s = 1,25 d.
Среднее квадратическое отклонение играет важную роль в анализе вариационных рядов распределения. В условиях нормального распределения существует следующая взаимосвязь между величиной среднего квадратического отклонения и количеством наблюдений:
· В пределах x + 1s располагается 0,683, или 68,3% количества наблюдений;
· В пределах х + 2s - 0,954, или 95,4%;
· В пределах х + 3s - 0,997, или 99,7% количества наблюдений.
В действительности на практике почти не встречаются отклонения, которые превышают +3s. Отклонение 3s может считаться максимально возможным. Это положение называют правилом трех сигм.
Дисперсия – представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и в зависимости от исходных данных вычисляется по формулам простой дисперсии и взвешенной дисперсии.
Пример. Рассмотрим расчет дисперсии и среднего квадратического отклонения по данным нижеприведенной таблицы о выпуске промышленной продукции фирмами отрасли.
Вычисление s и s по несгруппированным данным
| Номер фирмы | Выпущено промышленной продукции за год, млн.руб. х | x i - x | х i - х) |
| А | |||
| +10 +2 -10 +10 -12 | |||
| Итого | __ |
Алгоритм расчета следующий:
- Определим среднюю величину по исходным данным (графа 1) по формуле средней арифметической простой:
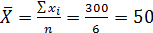 .
.
- Найдем отклонения (x i - х) и запишем их в графе 2.
Пример. Вычислить дисперсию:
Произведено продукции одним рабочим, шт. (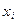 варианта) варианта)
| Число рабочих, 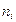
| 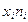
| 
| 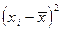
| 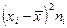
|
| -2 | |||||
| ИТОГО |
Исчислим среднюю арифметическую взвешенную:
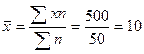 шт.
шт.
Значения отклонений от средней и их квадратов представлены в таблице. Определим дисперсию:
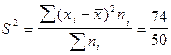 =1,48
=1,48
Среднее квадратическое отклонение будет равно:
 шт.
шт.
Пример. Рассчитать дисперсию для интервального ряда по данным о распределении посевной площади по урожайности пшеницы:
| Урожайность пшеницы, ц/га | Посевная площадь, га | 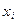
| 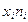
| 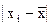
| 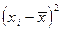
| 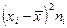
|
| 14 - 16 | -3,4 | 11,56 | ||||
| 16 - 18 | -1,4 | 1,96 | ||||
| 18 - 20 | 0,6 | 0,36 | ||||
| 20 - 22 | 2,6 | 6,76 | ||||
| ИТОГО |
Средняя арифметическая равна:
 ц с 1га.
ц с 1га.
Исчислим дисперсию:
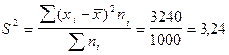
Важнейшие математические свойства дисперсии:
· Если от всех вариант отнять какое-то постоянное число А, то дисперсия не изменится. Это значит, что дисперсию можно вычислить не по заданным вариантам, а по отклонениям их от какого-то постоянного числа.
· Если все значения вариант разделить на какое-то постоянное число А, то дисперсия уменьшится в  раз, а среднее квадратическое отклонение – в А раз. Значит, можно разделить все варианты на какое-то постоянное число, исчислить среднее квадратическое отклонение, а затем умножить на это постоянное число.
раз, а среднее квадратическое отклонение – в А раз. Значит, можно разделить все варианты на какое-то постоянное число, исчислить среднее квадратическое отклонение, а затем умножить на это постоянное число.
· Если исчислить дисперсию от любой величины А, отличающейся от средней арифметической, то она всегда будет больше дисперсии, исчисленной от средней арифметической, причем на величину квадрата разности между средней и величиной А. Это значит, что дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, то есть она имеет свойство минимальности.
· Дисперсия равна разности между средним квадратом значений и квадратом среднего значения признака. Этим способом расчета дисперсии широко пользуются на практике.
В статистическом исследовании очень часто бывает необходимо не только изучить вариации признака по всей совокупности, но и проследить количественные изменения признака по однородным группам совокупности, а также и между группами. Следовательно, помимо общей средней для всей совокупности необходимо просчитывать и частные средние величины по отдельным группам.
Различают четыре вида дисперсий:
- общая;
- межгрупповая;
- внутригрупповая (частная);
- дисперсия средняя из внутригрупповых.
Общая дисперсия ( ) характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию, а именно: влияние признака-фактора, положенного в основание группировки и влияние других незначительных факторов. Эта величина определяется по формулам:
) характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию, а именно: влияние признака-фактора, положенного в основание группировки и влияние других незначительных факторов. Эта величина определяется по формулам:
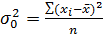 - простая.
- простая.
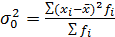 – взвешенная
– взвешенная
Межгрупповая дисперсия (дисперсия групповых средних) характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Эта дисперсия рассчитывается по формуле:

Внутригрупповая (частная) дисперсия:
 .
.
Дисперсия средняя из внутригрупповых определяет случайную вариацию результативного признака, обусловленную влиянием неучтенных факторов. Эта дисперсия рассчитывается по формуле:

Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:

Это тождество отражает закон (правило) сложения дисперсии. Опираясь на это правило, можно определить, какая часть (доля) общей дисперсии складывается под влиянием признака-фактора, положенного в основу группировки.
Правило сложения дисперсий легло в основу расчета коэффициента детерминации и эмпирического корреляционного отношения, используемых при изучении связей между явлениями.
Коэффициент детерминации рассчитывается как отношение межгрупповой дисперсии к общей дисперсии. Он показывает, какую долю общей вариации признака составляет вариация, обусловленная фактором, положенным в основание группировки.
Этот показатель характеризует тесноту связи.
Если коэффициент детерминации:
- равен нулю, то фактор-признак не оказывает влияния на результативный признак.
– равен единице, то изменение результативного признака полностью обусловлено изменением факторного признака.
- меньше 0,3, то связь невыражена;
- от 0,3 до 0,5, то связь слабая;
- от 0,5 до 0,7, то связь умеренная (средняя);
- от 0,7 до 0,9, то связь сильная
- от 0,9 до 0,99, то связь тесная.
Эмпирическое корреляционное отношение рассчитывается как корень квадратный из коэффициента детерминации. Оно характеризует тесноту связи. Этот показатель позволяет оценит степень влияния факторного признака на результативный.
Если эмпирическое корреляционное отношение
- равно 0, то факторный признак не оказывает влияния на образование общей вариации, т. е. на результативный признак;
- равно 1, то факторный признак полностью обуславливает изменение результативного признака, т. е. между ними существует функциональная связь.
2.6 Оценка вариационного ряда на асимметрию и эксцесс
Асимметрия и эксцесс являются важнейшими характеристиками формы распределения.
Ряды распределения могут иметь один и тот же центр группирования (показатели центра распределения) и одинаковые пределы варьирования признака (показатели вариации), однако при этом отличаться характером распределения единиц совокупности вокруг центра.
Для оценки степени асимметричности применяют моментный и структурный коэффициенты асимметрии.
Моментный коэффициент асимметрии (стандартизованный момент третьего порядка) определяется по формуле:
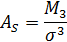
где М3 – центральный момент третьего порядка.
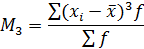
На направление асимметрии указывает знак коэффициента: если он отрицательный, то это левосторонняя асимметрия, при правосторонней асимметрии знак положителен.
Степень существенности асимметрии можно оценить с помощью средней квадратической ошибки коэффициента асимметрии, которая зависит от объема изучаемой совокупности и рассчитывается по формуле:
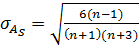 ,
,
Основной недостаток моментного коэффициента асимметрии заключается в том, что его величина зависит от наличия в совокупности резко выделяющихся единиц. Для таких совокупностей этот коэффициент малопригоден, поскольку его большая (абсолютная) величина будет объяснятся доминирующим вкладом в величину центрального момента третьего порядка нетипичных значений, а не асимметричностью распределения основной части единиц. В таких случаях рекомендуют либо исключить из анализа резко отличающиеся единицы, либо использовать структурные показатели асимметрии.
Структурные показатели (коэффициенты) асимметрии характеризуют асимметричность только в центральной части распределения, т. е. основной массы единицы, и в отличие от моментного коэффициента не зависят от крайних значений признака.
Наиболее часто применяют структурный коэффициент асимметрии, предложенный английским статистиком К. Пирсоном:
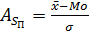 .
.
Другим свойством рядов распределения является эксцесс. Под эксцессом понимают островершинность или плосковершинность распределения по сравнению с нормальным распределением при той же силе вариации. Другими словами, эксцесс – это отклонение вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. При этом эксцесс определяется только для симметричных и умеренно ассиметричных распределений.
Чаще всего на практике эксцесс оценивается с помощью следующего показателя:
 ,
,
где М4 – центральный момент четвертого порядка.

Формула эксцесс основана на отклонение от нормального распределения (в нормальном распределении отношение М4:  =3).
=3).
Положительный эксцесс свидетельствует о том, что в совокупности есть слабоварьирующее по данному признаку "ядро", а в плосковершинных распределениях такого "ядра" нет и единицы рассеян по всем значениям признака более равномерно.
Чтобы оценить существенность эксцесса распределения, рассчитывают среднюю квадратическую ошибку эксцесса:
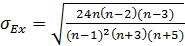 .
.
Список использованной литературы
1. Акулич М. В. Статистика в таблицах, формулах и схемах. – СПб.: Питер, 2009. – 128 с.
2. Статистика: учеб. / И. И. Елисеева. – М.: ТК Велби, Изд-во Проспект, 2006. – 448 с.
3. Статистика: учебник / Н. В. Толстик, Н. М. Матегорина. – Изд. 4-е, дополн. и перераб. – Ростов н/Д: Феникс, 2007. – 344 с.
4. www.aup.ru
5. www.chaliev.narod.ru
6. www.hi-edu.ru
7. www.markeloff.ru
|
|
Дата добавления: 2015-06-26; Просмотров: 3038; Нарушение авторских прав?; Мы поможем в написании вашей работы!