Алгебра операторов

Алгебра операторов. Обозначения. Равенство операторов. Операции с операторами. Коммутатор. Линейный оператор. Эрмитовский оператор. Обратный оператор. Примеры линейных и эрмитовских операторов.

Каждой физической величине можно сопоставить линейный эрмитов оператор. Оператор можно определить как функцию функции. На самом деле, функция есть закон, по которому значению (численному) одной переменной ставится в однозначное соответствие численное же значение другой переменной. Также и оператор, только роль переменных здесь выполняют функции. То есть оператор есть закон, по которому одной функции ставится в однозначное соответствие другая функция. Рассмотрим примеры. 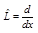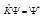Оператор ставит функции в однозначное соответствие её производную: , ; оператор ставит в соответствие функции 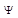сопряжённую ей функцию ; и т. д. Рассмотрим некоторые характеристики операторов. Оператор называется линейным, если для любых выполняется следующее равенство: .

В силу принципа суперпозиции в квантовой механике используются линейные операторы.

Линейный оператор – это такой оператор действующий на , что

(1) 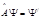(2) здесь – задача Штурма-Лиувилля - 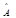действует на произвольную функцию .

Линейность: Если , то (3) т.к. , то из (3)

Сопряженный оператор – это оператор, который связан с данным оператором соотношением:

или Отсюда Если - то оператор называется эрмитовым.

Транспонированный оператор

Отметим следующие свойства:

1) , (4)

Из выражения (4) получаем 2) 3)

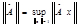
Сумма операторов: . Это операторное равенство предполагает

Произведение операторов: , тогда . Это операторное равенство предполагает

В общем случае не коммутативны

Коммутатор

Если , то операторы коммутативны.

Если , то операторы не коммутативны.

Так как физические величины вещественны, то число операторов в квантовой механике сужается.

Сужение класса операторов – эрмитовость операторов.

Запишем определение среднего:

Так как результаты измерений вещественны, то тоже должно быть вещественным, т.е.

(5)

Тогда , т.е.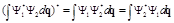

Обозначим , тогда

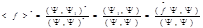
Тогда из (5) получаем

(6)

Из (6) имеем для любых : , , 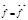где (сопряженный и транспонированный)

Каждой физической величине можно сопоставить линейный эрмитов оператор. Оператор можно определить как функцию функции. На самом деле, функция есть закон, по которому значению (численному) одной переменной ставится в однозначное соответствие численное же значение другой переменной. Также и оператор, только роль переменных здесь выполняют функции. То есть оператор есть закон, по которому одной функции ставится в однозначное соответствие другая функция. Рассмотрим примеры. Оператор 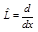ставит функции в однозначное соответствие её производную: , ; оператор ставит в соответствие функции сопряжённую ей функцию ; и т. д. Рассмотрим некоторые характеристики операторов. Оператор называется линейным, если для любых выполняется следующее равенство: .

2. Собственный функции и собственные значения операторов. Спектр операторов. Вырождение. Степень вырождения. Примеры решения задачи на для определения спектра оператора и его собственной функции.

В квантовой теории наблюдаемым ставятся в соответствие эрмитовы операторы в гильбертовом пространстве чистых состояний квантовой системы. При этом измерение интерпретируется как такое взаимодействие квантовой системы с измерительным прибором, в результате которого она переходит в состояние, описываемое Собственным Вектором наблюдаемой. Результатом измерения является Собственное Значение.

Определение: Если существуют такие значения числа f, при которых уравнение имеет нетривиальные решения, то они называются СЗ оператора F, а эти решения называются СВ этого оператора, соответствующими этим СЗ.

Основные свойства:

-все СЗ эрмитова оператора вещественны

-СВ эрмитова оператора, отвечающие разным СЗ, ортогональны

-два эрмитовых оператора имеют общую полную систему СВ тогда и только тогда, когда они коммутируют

-в Н существует ПОБ, составленный из СВ любого эрмитова оператора с чисто дискретным спектром. В случае непрерывного спектра можно построить расширение пространства, в котором такой базис тоже будет существовать.

Максимально широкий набор попарно коммутирующих независимых наблюдаемых называется Полным Набором Наблюдаемых для данной системы. Количество операторов в ПНН – число степеней свободы системы. Каждому набору СЗ операторов ПНН отвечает один и только один (с точностью до фазового множителя) их общий нормированный СВ.

Дата добавления: 2015-06-04