Теоремы для эрмитовских операторов

Теоремы для эрмитовских операторов.(полный набор собественных функций, свойства собственных чисел, свойства собственных функций коммутирующих операторов, орнормировка).

Оператор называется эрмитово сопряжённым по отношению к оператору , если для любых функций и 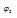из пространства выполняется равенство: . Такая запись эквивалентна следующему соотношению: 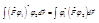Оператор 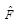называется эрмитовым, если . Физическая величина может принимать только те значения, которые принадлежат спектру её операторов. Если результатом действия оператора на функцию является число, умноженное на эту же функцию , то такая функция называется собственной функцией оператора , а число 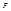- собственным значением этого оператора. Вообще говоря, оператор может иметь несколько собственных функций и собственных значений, поэтому правильнее использовать запись 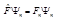. Совокупность всех собственных значений оператора называют его спектром. Здесь может пробегать как дискретный, так и непрерывный ряд значений. Выясним теперь, какие ограничения накладывает на собственные функции эрмитовость оператора.

Теорема I. Все собственные значения эрмитового оператора действительны. Умножим слева равенство 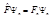на функцию и проинтегрируем результат: 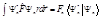(2) Рассмотрим левую часть этого выражения. По определению эрмитова оператора мы можем записать для

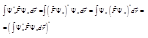: (3) последнее равенство следует из теории операторов (в данном курсе не рассматривается). Теперь, сравнивая выражение справа в (3) и выражение слева в (2), видим что 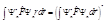(4) Из выражения (4) следует, что, так как число слева равно своему сопряжённому, то это число действительное. Таким образом, теорема доказана.

Теорема II. Собственные функции линейного эрмитова оператора, принадлежащие различным собственным значениям, ортогональны друг другу, то есть , если , . Запишем по определению собственного значения: (5) Из условия самосопряжённости мы можем записать: 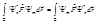. Теперь, подставляя сюда формулы (5), получим: 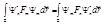. Так как 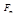и – константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим: , . По условию , поэтому, .

Дата добавления: 2015-06-04