Рівняння руху в нерелятивістській квантовій механіці. Рівняння Шредінґера

Нерелятивістська квантова механіка – це розділ квантової теорії, який не включає релятивістські ефекти, коли швидкості частинок порівнянні зі швид­кістю світла. Як відомо, стан квантової системи задається хвильовою функцією 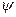. Розглянемо тепер питання, яким чином описується зміна станів квантових систем з плином часу, тобто, як маючи хвильову функцію квантової системи у початковий момент часу, знайти її у всі наступні моменти?

Як і при встановленні рівнянь Ньютона у класичній механіці або рівнянь Максвелла у класичній електродинаміці, ми не виводимо рівняння руху кванто­вої механіки, а постулюємо його на основі загальних принципів і деяких конкретних припущень. Таким чином, вважатимемо, що рівняння, яке описує зміну станів квантово-механічних систем у часі, має вигляд

, (5.16)

де 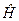– оператор Ґамільтона квантової системи. Це рівняння називають хвильо­вим рівнянням Шредінґера або просто хвильовим рівнянням. Воно є базовим рівнянням квантової механіки.

Запишемо рівняння (5.16) для випадку системи N>1 частинок:

, (5.17)

де

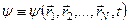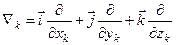, , (5.18)

а

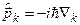, , (5.19)

де – оператор імпульсу k -вої частинки, m_k – її маса, U – потенціальна енер­гія, яка містить як взаємодію частинок із зовнішнім полем, так і їх взаємодію між собою, k =1, 2,…, N.

Всі наступні розділи квантової механіки, які ми будемо вивчати, пов’язані з рівнянням Шредінґера. Розв’язки цього рівняння, а також висновки з них блискуче пояснюють експериментальні факти і явища квантової фізики. Зрозу­міло, що не для всіх цікавих задач рівняння Шредінґера має точні розв’язки. Через це створена ціла низка наближених методів розв’язання цього рівняння. Їх використання дало змогу зрозуміти багато цікавих явищ природи.

Що стосується самого рівняння Шредінґера, то ще раз підкреслимо, що воно не виводиться, а постулюється. При цьому просторові координати (x, y, z) і час t входять у це рівняння несиметричним чином. Задачі, які мають точний розв’язок ми розглянемо дещо пізніше.

Стаціонарні стани. Стаціонарне рівняння Шредінґера

Розглянемо систему, у якої оператор Ґамільтона 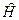явно не залежить від часу, тобто

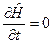. (5.20)

У цьому випадку хвильове рівняння Шредінґера (5.16) допускає розв’язки з відокремленими змінними:

. (5.21)

Оператор Ґамільтона 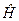не залежить від часу, тому

, (5.22)

або

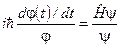. (5.23)

Ліва частина цього рівняння є функцією лише часу t, а права – тільки координат q. Рівність, очевидно, виконується, якщо ліва і права частини рівняння дорів­нюють деякій сталій величині, яку ми позначимо через E:

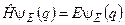, (5.24)

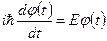. (5.25)

Перше з цих рівнянь є рівнянням на власні функції і власні значення оператора Ґамільтона 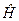, який є оператором енергії, отже, величина E має зміст енергії. Рівняння (5.24) називають також стаціонарним рівнянням Шредінґера. Хвильо­ві функції відповідають станам системи, у яких енергія має певне значен­ня.

Розв’язок іншого рівняння, а саме (5.25), можна записати у такому вигляді:

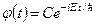. (5.26)

У квантовій механіці стани з певним значенням енергії називають ста­ціонарними станами. Для оператора 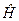з дискретним спектром власних значень E_n, n =1,2,…, і відповідних їм власних функцій 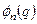стаціонарні стани з певною енергією E_n описуються хвильовими функціями

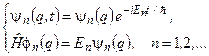. (5.27)

Система функцій 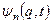є повною (замкненою), і будь-яка хвильова функція може бути представлена у вигляді

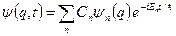, (5.28)

а величина 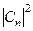рівна імовірності значення енергії E_n.

Якщо оператор 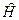має неперервний спектр власних значень, тоді

, (5.29)

а величина 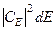визначає імовірність того, що система має енергію, значення якої містяться в інтервалі значень (E, E + dE).

Розв’язування стаціонарного рівняння Шредінґера – це одна з центральних задач квантової механіки. Адже енергетичний спектр квантовомеханічних сис­тем (множина власних значень оператора 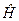) є найважливішою фізичною ха­рактеристикою системи (наприклад, атома водню, атома/іона гелію і т. д.). Ду­же важливим є також знання хвильових функцій . Вони дозволяють розра­ховувати середні значення спостережуваних фізичних величин, визначати просторову структуру атомів у їх різних власних станах. За допомогою хвильо­вих функцій проводять розрахунки імовірностей переходів між станами, інтенсивностей випромінювання й поглинання атомами світла, перерізів роз­сіяння одних атомних частинок на інших, тощо.

Розглянуті у попередній лекції приклади операторів Ґамільтона для потен­ціальної ями, гармонічного осцилятора, атома водню і атома гелію відносяться до випадку, коли оператор Ґамільтона явно не залежить від часу, а тому запи­са­ні там рівняння на власні значення і власні функції відповідних операторів Ґамільтона є стаціонарними рівняннями Шредінґера для перерахованих кванто­вих систем. Перші три з цих задач (за винятком атома гелію) мають точний розв’язок. Він існує також для задачі про проходження частинки через потен­ціальний бар’єр. У більшості задач квантової механіки та­ких розв’язків просто не існує.

Атом водню у довільному зовнішньому електромагнітному полі. Розглянемо ще один приклад стаціонарного рівняння Шредінґера для атома водню у до­вільному зовнішньому електромагнітному полі з потенціалами і . У класичній механіці функція Ґамільтона для електрона у полі „нерухомого” ядра (класично спрощена модель атома водню) має вигляд:

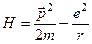, (5.30)

де m та e – відповідно, маса та заряд електрона, r – віддаль електрона від ядра "Вмикання" зовнішнього електомагнітного поля з потенціалами і у класичній електродинаміці здійснюється двома одночасними замінами: 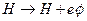і . Відповідно до цього, у квантовій механіці слід зробити такі зсуви операторів:

(отже, ) та . (5.31)

Внаслідок цього нестаціонарне рівняння Шредінґера для розглядуваного випадку матиме вигляд:

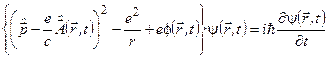. (5.32)

Дата добавления: 2015-06-04