
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Конец четвертой лекции
|
|
|
|
Наверное, каждый видел, как ловят рыбу спиннингом. Забрасывают подальше от берега в воду блесну — похожую на маленькую рыбку металлическую приманку с крючком, – а затем быстро сматывают на катушку леску, к которой она привязана. Чаще всего блесна возвращается обратно пустой, но иногда на крючке бьется хищная рыба — окунь, судак или щука, принявшая приманку за настоящую рыбку.
Сколько раз придется забрасывать блесну, чтобы поймать 1 рыбку? Это зависит от времени года, времени суток, погоды. Рыболов может сказать, что в среднем необходимо десять забросов. Тогда вероятность 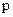 поймать рыбу за один заброс равна 0,1, а вероятность вытянуть пустой крючок
поймать рыбу за один заброс равна 0,1, а вероятность вытянуть пустой крючок 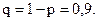 А какова вероятность за сто забросов не поймать ни одной рыбы? Или поймать 10 рыб?
А какова вероятность за сто забросов не поймать ни одной рыбы? Или поймать 10 рыб?
Похожая ситуация возникает, когда подбрасывают монету и считают, сколько раз выпадет орел. Ясно, что вероятность появления орла при каждом бросании 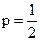 , как и вероятность выпадения решки
, как и вероятность выпадения решки 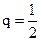 . А какова вероятность того, что при десяти бросаниях орел выпадет, например, пять раз? Или восемь раз?
. А какова вероятность того, что при десяти бросаниях орел выпадет, например, пять раз? Или восемь раз?
Такая процедура носит название схемы Бер-нулли — по имени уже известного нам швейцарского математика Якоба Бернулли, предложившего и изучившего ее. Давайте познакомимся с ней поближе.
Пусть производится 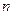 независимых испытаний и в каждом из них удача имеет вероятность
независимых испытаний и в каждом из них удача имеет вероятность 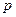 , а неудача — вероятность
, а неудача — вероятность 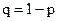 . Тогда количество успешных испытаний
. Тогда количество успешных испытаний 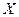 из общего числа испытаний
из общего числа испытаний 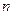 есть случайная величина, которая может принимать
есть случайная величина, которая может принимать 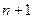 значение:
значение: 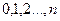 . Каково ее распределение? Другими словами, какова вероятность
. Каково ее распределение? Другими словами, какова вероятность 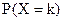 того, что в
того, что в 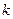 испытаниях нам будет сопутствовать удача, а в остальных
испытаниях нам будет сопутствовать удача, а в остальных 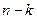 испытаниях постигнет неудача?
испытаниях постигнет неудача?
Выберем какие-нибудь конкретные 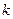 испытаний. Пусть это испытания с номерами
испытаний. Пусть это испытания с номерами 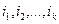 . Вероятность того, что испытание
. Вероятность того, что испытание 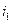 закончится успешно, равна
закончится успешно, равна 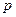 . Аналогично, вероятность того, что испытание
. Аналогично, вероятность того, что испытание 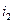 будет успешно, равна
будет успешно, равна 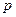 и т. д. С другой стороны, вероятность того, что испытание
и т. д. С другой стороны, вероятность того, что испытание  окажется неудачным, равна
окажется неудачным, равна 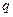 (здесь
(здесь 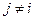 ни в каких случаях). Значит, вероятность того, что и испытание
ни в каких случаях). Значит, вероятность того, что и испытание 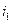 и испытание
и испытание 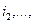 и испытание
и испытание 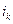 завершатся успехом, а все остальные испытания — неудачей, равна
завершатся успехом, а все остальные испытания — неудачей, равна 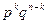 , так как вероятность произведения независимых событий равна произведению их вероятностей.
, так как вероятность произведения независимых событий равна произведению их вероятностей.
|
|
|
Но мы рассмотрели лишь один вариант выбора 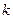 успешных испытаний из общего числа испытаний. Всего же таких вариантов, как учит комбинаторика, существует
успешных испытаний из общего числа испытаний. Всего же таких вариантов, как учит комбинаторика, существует 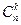 . Поэтому вероятность того, что успешными будут какие-то
. Поэтому вероятность того, что успешными будут какие-то 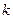 испытаний, а все остальные испытания будут неудачны, равна
испытаний, а все остальные испытания будут неудачны, равна 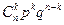 .
.
Таким образом, вероятность 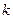 успешных исходов
успешных исходов 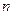 испытаний по схеме Бернулли можно выразить формулой, носящей имя Бернулли:
испытаний по схеме Бернулли можно выразить формулой, носящей имя Бернулли:
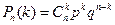 . (1.23)
. (1.23)
Поэтому распределение вероятностей 1.23 носит название биномиального распределения.
Теперь попробуем ответить на вопросы о монете и рыбках. В случае бросания монеты 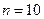 ,
, 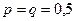 ,
, 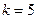 или 8.
или 8.
Применяя формулу (1.24), получим:
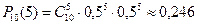 ,
,
и
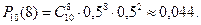
В задаче с рыболовом 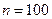 ,
, 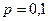 и
и 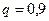 , а
, а 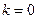 или 10. Тогда, рассуждая аналогично предыдущему, получим:
или 10. Тогда, рассуждая аналогично предыдущему, получим:
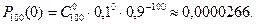
Если рыболов не поймает ни одной рыбы, то совершенно очевидно, что он вероятность успеха ( 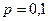 ) оценил неверно.
) оценил неверно.
B случае 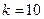 получаем
получаем 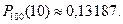
Схема Бернулли применима как для 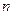 последовательно, так и для
последовательно, так и для 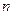 одновременно проводимых испытаний. Например, десятикратное подбрасывание 1 монеты можно заменить однократным подбрасыванием 10 монет. Используем это обстоятельство для решения одной жизненно важной задачи.
одновременно проводимых испытаний. Например, десятикратное подбрасывание 1 монеты можно заменить однократным подбрасыванием 10 монет. Используем это обстоятельство для решения одной жизненно важной задачи.
Предположим, вы решили полететь на самолете в Саратов и у вас есть выбор: лететь на двухмоторном или на четырехмоторном самолете. Моторы у самолетов одинаковы, и каждый с вероятностью 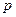 может отказать во время полета. От знакомых авиаторов вы знаете, что двухмоторный самолет способен долететь до Саратова и на одном моторе, а четырехмоторный — на трех или даже на двух моторах, а на одном уже не может. Какой самолет надежнее?
может отказать во время полета. От знакомых авиаторов вы знаете, что двухмоторный самолет способен долететь до Саратова и на одном моторе, а четырехмоторный — на трех или даже на двух моторах, а на одном уже не может. Какой самолет надежнее?
|
|
|
Обозначим через 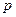 вероятность выхода мотора из строя за время полета, а через
вероятность выхода мотора из строя за время полета, а через 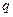 — вероятность безотказной работы двигателя. Тогда вероятность катастрофы двухмоторного самолета равна
— вероятность безотказной работы двигателя. Тогда вероятность катастрофы двухмоторного самолета равна 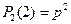 , а четырехмоторного —
, а четырехмоторного — 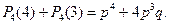
Определим, при каких значениях 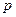 и
и 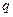 вероятность разбиться на двухмоторном самолете будет меньше, чем на четырехмоторном, т. е. когда
вероятность разбиться на двухмоторном самолете будет меньше, чем на четырехмоторном, т. е. когда 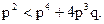 Очевидно, что
Очевидно, что 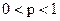 . Сократив на
. Сократив на 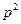 и заменив
и заменив 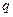 на
на 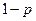 , получим, что вероятность разбиться на двухмоторном самолете будет меньше, если
, получим, что вероятность разбиться на двухмоторном самолете будет меньше, если 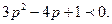 Это неравенство справедливо при
Это неравенство справедливо при 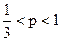 .
.
Те же авиаторы вам сообщили, что для моторов, которые установлены на таких самолетах, 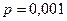 , что, конечно же, меньше
, что, конечно же, меньше 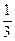 . А потому полет на четырехмоторном самолете является более безопасным.
. А потому полет на четырехмоторном самолете является более безопасным.
Глава 1.11. Случайные величины и их числовые характеристики
В теории вероятностей часто рассматривают случайные события, которые характеризуются числами: количество покупателей в супермаркете за промежуток времени, напряжение в сети, показания приборов в эксперименте и др. Такие события называются случайными величинами. А раз это числа, то их можно складывать, умножать на обычные числа и т. д. Да и другие случайные события иногда можно трактовать как числа. Например, выпадению той или иной грани игрального кубика соответствует число на этой грани. Выпадение орла при подбрасывании монеты можно обозначить через 1, а выпадение решки — через 0. Тогда сумма значений такой случайной величины при 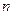 подбрасываниях монеты равна числу выпавших орлов.
подбрасываниях монеты равна числу выпавших орлов.
Вообще, если случайная величина 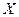 может принимать значения
может принимать значения 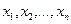 , то значения
, то значения 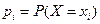 , где
, где 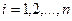 , называются распределением вероятностей случайной величины
, называются распределением вероятностей случайной величины 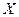 , причем справедливо равенство
, причем справедливо равенство
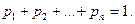
На практике распределение случайной величины задают в виде таблицы, у которой первой строкой идут значения случайной величины, а второй строкой – вероятности с которыми эти значения принимаются. Например, в случае с подбрасыванием игральной кости – закон распределения числа выпавших очков будет иметь вид таблицы 1.1.
Таблица 1.1
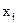
| ||||||
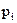
| 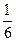
| 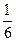
| 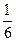
| 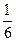
| 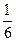
| 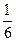
|
Во многих случаях важно знать «среднее значение» случайной величины. В теории вероятностей оно называется математическим ожиданием и определяется следующим образом.
|
|
|
Пусть случайная величина 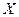 может принимать значения
может принимать значения 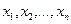 с вероятностями
с вероятностями 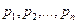 соответственно. Тогда число
соответственно. Тогда число
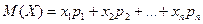 (1.25)
(1.25)
есть математическое ожидание случайной величины 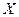 .
.
Если вычислить математическое ожидание числа очков, выпавших при подбрасывании игральной кости, представленное в таблице 1.1, то оно будет задано суммой произведений значений на соответствующие вероятности, т. е.
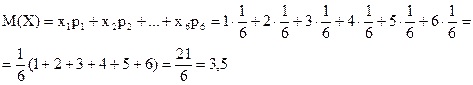
Если изобразить закон распределения числа очков, выпавших при подбрасывании игральной кости графически, где по оси абсцисс отложить значения случайной величины, а по оси ординат им соответствующие вероятности, то график будет представлять собой прямую линию, параллельную оси абсцисс. Такое распределение называют равномерным. Математическое ожидание в этом случае будет представлено точкой с координатой 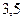 на оси абсцисс.
на оси абсцисс.
Понятие математического ожидания, которое получило дальнейшее развитие в трудах Даниила Бернулли, Даламбера и др., первым ввел Гюйгенс. Он писал, что математическим ожиданием игрока, имеющего вероятность 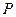 для выигрыша суммы
для выигрыша суммы 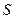 , является произведение
, является произведение 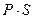 .
.
Например, лотерейный розыгрыш некоторого ценного объекта стоимостью в 3 000 руб. при выпуске 1 000 билетов ценою в 3 руб. каждый является справедливым, так как вероятность выигрыша каждого билета есть 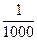 , а математическое ожидание покупателя равно
, а математическое ожидание покупателя равно 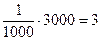 именно столько, сколько он уплатил за лотерейный билет. Если количество выпущенных билетов было бы больше 1 000, то при сохранении всех остальных условий игра уже не была бы справедливой. Тогда математическое ожидание выразилось бы формулой (1.25).
именно столько, сколько он уплатил за лотерейный билет. Если количество выпущенных билетов было бы больше 1 000, то при сохранении всех остальных условий игра уже не была бы справедливой. Тогда математическое ожидание выразилось бы формулой (1.25).
Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:
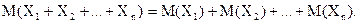 (1.26)
(1.26)
Если 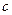 — постоянная (т. е.
— постоянная (т. е. 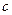 есть случайная величина, всегда принимающая одно и то же значение), то
есть случайная величина, всегда принимающая одно и то же значение), то
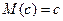 и
и  . (1.27)
. (1.27)
Понятие математического ожидания находит немало применений в разных других областях человеческой деятельности. Но вернемся снова к анализу азартных игр. Игра на деньги или жетоны называется безобидной, если математическое ожидание выигрыша для каждого игрока равно 0. В противном случае она выгодна тому игроку, для которого математическое ожидание выигрыша положительно.
|
|
|
Рассмотрим всем известную игру с подбрасыванием монеты. Один из игроков делает ставку на орла, а второй — на решку. Монету подбрасывают. Если она упадет орлом, то второй платит первому, например, рубль, а если решкой — первый платит второму рубль. Так как вероятности выпадения и орла, и решки равны 0,5, то математическое ожидание выигрыша любого игрока равно нулю, т. е.: 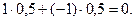
Значит, игра безобидная.
Игрок в рулетку, поставивший 1 жетон, например, на линию, выигрывает 5 жетонов с вероятностью 6/37 и проигрывает 1 жетон с вероятностью 31/37. Поэтому математическое ожидание его выигрыша равно:
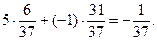
Игра явно небезобидная и выгодна игорному дому, который с каждого поставленного жетона имеет выигрыш 1/37 жетона.
Несколько более сложна игра «Попытай счастье», в которую играли в XIX в. на североамериканском Дальнем Западе. Бармен предлагал скучающему посетителю поставить доллар и назвать одно из чисел: 1, 2, 3, 4, 5, 6. «Теперь ты бросаешь три игральные кости, — продолжал он. — Если на одной из них выпадет названное тобой число, то забирай свой доллар и еще один мой в придачу. Если это число выпадет на двух костях, то я к твоему доллару доплачу еще два. А если на всех трех, то я даю три доллара».
Безобидна ли эта игра, и если нет, то кому выгодна? Вероятность выпадения нужного числа при бросании одной кости 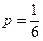 , а вероятность невыпадения
, а вероятность невыпадения 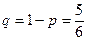 . Расчеты показывают: вероятность того, что ни разу не выпадет названное число, равна:
. Расчеты показывают: вероятность того, что ни разу не выпадет названное число, равна:
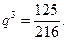
Вероятность выпадения нужного числа ровно на 1 кости
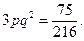
Вероятность выпадения этого числа ровно на двух костях будет найдена как
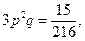
а вероятность тройного успеха
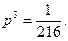
Тогда
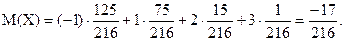
Значит, посетителю игра не выгодна.
Если число испытаний 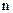 достаточно велико, а вероятность появления события
достаточно велико, а вероятность появления события 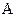 в каждом испытании мала
в каждом испытании мала 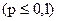 , то математическое ожидание числа появлений события
, то математическое ожидание числа появлений события 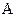 в
в 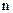 независимых испытаниях равно произведению числа испытаний на вероятность появления события
независимых испытаниях равно произведению числа испытаний на вероятность появления события 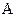 в каждом испытании.
в каждом испытании.
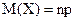 . (1.28)
. (1.28)
Например, найти математическое ожидание числа бракованных изделий в партии из 5000 изделий, если каждое изделие может оказаться бракованным с вероятностью 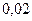 .
.
Так как число изделий велико, а вероятность брака в каждом изделии мала, то в соответствии с формулой 1.28 получим:
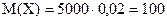 .
.
Если математическое ожидание является первой числовой характеристикой случайной величины, то разброс ее значений относительно математического ожидания — второй. Как оценить разброс? Из курса физики известно такое понятие дисперсии как – рассеивание света. В теории случайных величин мы сталкиваемся с аналогичным понятием.
Пусть 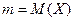 — математическое ожидание случайной величины
— математическое ожидание случайной величины 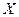 . Тогда
. Тогда 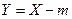 есть случайная величина, выражающая отклонение случайной величины
есть случайная величина, выражающая отклонение случайной величины 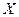 от ее математического ожидания. Первое, что приходит в голову, — вычислить математическое ожидание
от ее математического ожидания. Первое, что приходит в голову, — вычислить математическое ожидание 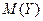 и принять полученный результат за характеристику разброса значений случайной величины
и принять полученный результат за характеристику разброса значений случайной величины 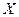 . Однако, согласно расчетам,
. Однако, согласно расчетам,
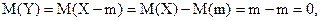
т. е. математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю. Если подумать, здесь нет ничего удивительного. Случайная величина 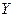 может принимать и положительные, и отрицательные значения, которые, в конце концов, уравновешивают друг друга.
может принимать и положительные, и отрицательные значения, которые, в конце концов, уравновешивают друг друга.
А что если рассмотреть квадрат отклонения случайной величины 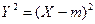 ? Во-первых, эта величина всегда неотрицательна, а во-вторых, она характеризует именно абсолютную величину отклонения, не зависящую от знака. Тогда
? Во-первых, эта величина всегда неотрицательна, а во-вторых, она характеризует именно абсолютную величину отклонения, не зависящую от знака. Тогда 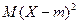 является математическим ожиданием квадрата отклонения случайной величины
является математическим ожиданием квадрата отклонения случайной величины 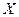 от ее математического ожидания. Оно называется дисперсией случайной величины
от ее математического ожидания. Оно называется дисперсией случайной величины 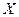 и обозначается
и обозначается 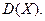
Для вычисления дисперсии пользуются утверждением, что она равна математическому ожиданию квадрата случайной величины без квадрата ее математического ожидания, т. е.
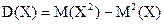 (1.29)
(1.29)
Предлагаем вычислить вам самостоятельно дисперсию числа выпавших очков при подбрасывании игральной кости по формуле 1.29. Приблизительно она будет равна 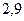 .
.
Дисперсия всегда неотрицательна, т. е.
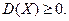
Причем, равенство 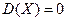 возможно в том и только в том случае, когда
возможно в том и только в том случае, когда 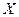 — постоянная (т. е. всегда принимает одно и то же значение). Дисперсия суммы независимых случайных величин равна сумме их дисперсий (как и для математического ожидания):
— постоянная (т. е. всегда принимает одно и то же значение). Дисперсия суммы независимых случайных величин равна сумме их дисперсий (как и для математического ожидания):
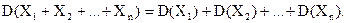 (1.30)
(1.30)
Если 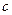 — постоянная величина, то
— постоянная величина, то
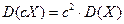 . (1.31)
. (1.31)
Следует отметить, что дисперсия имеет размерность, соответствующую квадрату размерности описываемой ею случайной величины. Поэтому очень часто используют другую характеристику:
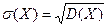 , (1.32)
, (1.32)
которую называют квадратичным отклонением случайной величины 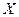 . Размерность
. Размерность 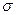 (сигма) та же, что и у
(сигма) та же, что и у 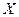 .
.
Если число испытаний 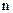 достаточно велико, а вероятность появления события
достаточно велико, а вероятность появления события 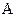 в каждом испытании мала
в каждом испытании мала 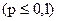 , то дисперсия числа появлений события
, то дисперсия числа появлений события 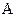 в
в 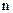 независимых испытаниях равно произведению числа испытаний на вероятность появления события
независимых испытаниях равно произведению числа испытаний на вероятность появления события 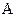 в каждом испытании и на вероятность не появления события
в каждом испытании и на вероятность не появления события 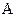 , т. е.
, т. е.
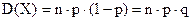 . (1.33)
. (1.33)
Проиллюстрируем понятия математического ожидания и дисперсии рассказом о «шулерской кости» — игральной кости, в которую вставлен свинцовый шарик. Он так расположен внутри кости, что вероятность выпадения той или иной грани кубика пропорциональна числу очков на этой грани.
Найдем вероятности выпадения различных граней кубика. Пусть 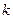 — коэффициент пропорциональности, тогда эти вероятности составляют:
— коэффициент пропорциональности, тогда эти вероятности составляют: 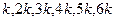 .
.
Их сумма должна быть равна 1, поэтому, 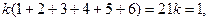 а значит,
а значит, 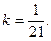
Подсчитаем математическое ожидание числа выпадающих очков:
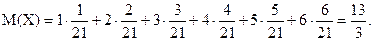
Теперь вычислим квадрат математического ожидания, т. е. 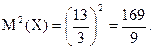
Далее найдем математическое ожидание квадратов значений случайной величины, т. е.
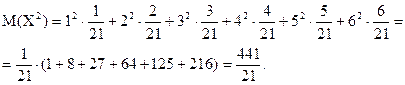
В соответствии с формулой 1.29, получим 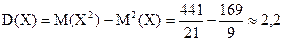 .
.
Заметим, что для обычного кубика (мы вычисляли ранее математическое ожидание 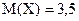 а дисперсию вы вычисляли самостоятельно и
а дисперсию вы вычисляли самостоятельно и 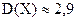 ).
).
Таким образом, у «шулерской кости» среднее число выпадающих очков ощутимо больше, а разброс меньше, чем у обычной игральной кости.
Как мы уже упоминали, в числе других Бернулли, повлиявших на развитие математики, есть два сына Иоганна: Николай и, особенно, Даниил. Николай, как и Даниил, был приглашен в Петербург, незадолго до того основанный Петром Великим; там он пробыл недолго. Даниил вместе с Л. Эйлером трудились в Петербургской академии.
Николай Бернулли предложил задачу по теории вероятностей, которая известна как Петербургская задача (или, более выразительно, Петербургский парадокс).
Во многих книгах по теории вероятностей имеются таблицы распределения Пуассона – французского математика и механика. Симеон Дени Пуассон (1781–1840 гг.) считал, что жизнь прекрасна благодаря лишь двум вещам — изучению математики и преподаванию математики.
Закон Пуассона действует всякий раз, когда имеется много независимых испытаний 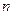 , а вероятность
, а вероятность 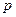 некоторого события
некоторого события 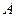 в каждом из них так мала, что среднее число событий
в каждом из них так мала, что среднее число событий 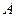 равное
равное 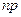 , невелико. Появление события
, невелико. Появление события 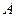 при данном испытании обычно называют исходом, а общее число событий
при данном испытании обычно называют исходом, а общее число событий 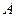 при
при 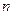 испытаниях — числом исходов
испытаниях — числом исходов 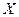 . В таком случае можно считать, что число исходов
. В таком случае можно считать, что число исходов 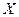 имеет распределение Пуассона с
имеет распределение Пуассона с 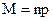 . Примерами может служить число дорожно-транспортных происшествий или число пожаров, произошедших за сутки в большом городе.
. Примерами может служить число дорожно-транспортных происшествий или число пожаров, произошедших за сутки в большом городе.
В самом деле, очень мала вероятность того, что за сутки данный автомобиль попадет в аварию или что в данном здании вспыхнет пожар. Однако 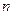 — число машин или зданий велико, а потому
— число машин или зданий велико, а потому 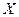 — число неприятных происшествий в большом городе подчиняется закону Пуассона. Это позволяет достаточно точно рассчитывать число машин «скорой помощи» или пожарных машин, чтобы, с одной стороны, вовремя оказать помощь, а с другой — не держать в резерве лишние машины. Конечно, в таких многомиллионных городах, как Москва, произведение
— число неприятных происшествий в большом городе подчиняется закону Пуассона. Это позволяет достаточно точно рассчитывать число машин «скорой помощи» или пожарных машин, чтобы, с одной стороны, вовремя оказать помощь, а с другой — не держать в резерве лишние машины. Конечно, в таких многомиллионных городах, как Москва, произведение 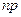 для мелких дорожно-транспортных происшествий без жертв или вызовов машин «скорой помощи», как правило, очень велико. В таком случае законом Пуассона целесообразно пользоваться при расчетах численности персонала и технической оснащенности служб помощи в отдельных районах города.
для мелких дорожно-транспортных происшествий без жертв или вызовов машин «скорой помощи», как правило, очень велико. В таком случае законом Пуассона целесообразно пользоваться при расчетах численности персонала и технической оснащенности служб помощи в отдельных районах города.
Для того чтобы нормально работать и получать прибыль, страховые компании во всем мире также прибегают к закону Пуассона. Пусть, например, страховая компания за страховку строения от пожара берет плату, равную 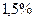 от суммы, на которую оно застраховано.
от суммы, на которую оно застраховано.
Предположим, что компания застраховала 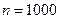 хозблоков на дачных участках на 8 тыс. рублей каждый. Собрав деньги за эту страховку в количестве 120 тыс. рублей, компания обязана выплатить за каждое сгоревшее в течение года строение 8 тыс. рублей. Если для хозблока вероятность сгореть в течение года равна
хозблоков на дачных участках на 8 тыс. рублей каждый. Собрав деньги за эту страховку в количестве 120 тыс. рублей, компания обязана выплатить за каждое сгоревшее в течение года строение 8 тыс. рублей. Если для хозблока вероятность сгореть в течение года равна 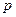 , то при небольших
, то при небольших 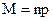 случайная величина
случайная величина 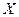 — число сгоревших за год застрахованных хозблоков — подчиняется распределению Пуассона. Компания разорится, если
— число сгоревших за год застрахованных хозблоков — подчиняется распределению Пуассона. Компания разорится, если 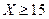 , поскольку в таком случае она должна выплатить погорельцам не менее 120 тыс. рублей, не говоря уже о других затратах. Расчет показывает, что
, поскольку в таком случае она должна выплатить погорельцам не менее 120 тыс. рублей, не говоря уже о других затратах. Расчет показывает, что
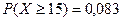 при
при 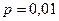 ,
,
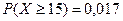 при
при 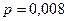 ,
,
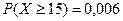 при
при 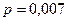 .
.
Исходя из этих вероятностей компании, видимо, невыгодно работать при 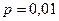 и вполне допустимо при
и вполне допустимо при 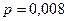 и
и 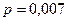 . Подобными, но более сложными расчетами занимается страховая, или, как ее еще называют, актуарная, математика. Раздел, который нами рассмотрен, имеет большое значение во всех направлениях деятельности, в том числе и экономической.
. Подобными, но более сложными расчетами занимается страховая, или, как ее еще называют, актуарная, математика. Раздел, который нами рассмотрен, имеет большое значение во всех направлениях деятельности, в том числе и экономической.
В завершении изучения этой лекции предлагаем выполнить оставшиеся задания 33-40 домашней контрольной работы.
После тщательной проверки всех ответов 40 заданий контрольной работы внимательно и аккуратно заполните таблицу ответов домашней контрольной работы.
Следующим этапом работы над курсом математики будет компьютерный практикум и выполнение контрольного компьютерного практикума.
Завершением изучения курса математики является контрольно-тестовый экзамен, состоящий из 100 тестовых заданий, на которые вам предстоит ответить.
Но прежде мы считаем необходимым рассказать о тех наградах, которых удостаивают математиков за открытия.
РАЗДЕЛ 2. ВЫСШИЕ НАГРАДЫ В ОБЛАСТИ МАТЕМАТИКИ
Научное открытие само по себе — величайшее счастье. Открыв законы движения планет, Иоганн Кеплер писал: «Я предаюсь радости и не стесняюсь похвалиться перед смертными: я похитил золотые сосуды египтян, чтобы создать из них храм моему божеству вдали от пределов Египта... Прочтется ли эта книга моими современниками или потомством — не столь уж важно, — она найдет своего читателя. Разве Господь Бог не ждал шесть тысяч лет созерцателя Своего творения?».
Труд ученого приносит величайшее удовлетворение, но в то же время человек, ищущий истину, нуждается в моральной, а часто и в материальной поддержке. Похвала и признание окрыляют, дают новые силы для работы, а потому и государственные структуры, и отдельные люди помогают ученым. Одна из форм такой поддержки — медали и премии за выдающиеся научные результаты.
Кто и когда впервые стал награждать ученых, ответить трудно. Но в XIX в. вручали уже достаточно много медалей и премий, и сами факты таких присуждений становились предметом национальной гордости. Одной из самых больших почестей, которых удостоились русские математики в XIX столетии, была премия Бордена Парижской академии наук. В 1888 г. ее вручили Софье Васильевне Ковалевской.
В настоящее время Российская Академия наук присуждает три медали и девять премий по математике: медали были учреждены в честь Л. Эйлера, П.Л. Чебышева и М.В. Келдыша; премии — имени И.М. Виноградова, С.В. Ковалевской, А.Н. Колмогорова, М.А. Лаврентьева, Н.И. Лобачевского, A.M. Ляпунова, А.И. Мальцева, А.А. Маркова (старшего) и И.Г. Петровского.
Интересна история премии Н.И. Лобачевского. Казанское физико-математическое общество поставило себе целью создать капитал для вручения международной премии имени Лобачевского.
На приглашение общества стать почетными членами комитета по организации 100-летнего юбилея со дня рождения великого русского геометра откликнулись математики Гельмгольц, Эрмит, Чебышев, Сильвестр, Клейн, Дарбу, Ли. Величайшие ученые того времени!
В пожертвованиях и сборе денег приняли участие и Лондонское королевское общество, и члены Французского факультета наук, и средние учебные заведения городов России, и персональные пожертвователи. Собрали 9 071 рубль 86 копеек. На эти средства устроили юбилейные торжества, поставили памятник Лобачевскому в Казани, а 6 000 рублей были объявлены неприкосновенным капиталом международной премии имени Н. И. Лобачевского. Вот строки из «Положения о премии»: «Основной капитал премии остается неприкосновенным на вечные времена …». Именно так – на вечные времена!
Первое присуждение состоялось в 1897 г. Премию (по отзыву Феликса Клейна) получил Софус Ли. Следующая премия (1900 г.) присуждена В. Киллингу. В 1903 г. премии удостоен Давид Гильберт. Отзыв на его работу писал Анри Пуанкаре. В 1906 г. премия вручена Б. Леви, а в 1909 г. – Л. Шлезингеру. В 1912 г. лауреатом стал Ф. Шур … и «вечные времена» закончились – разразилась Первая мировая война, а следом революция 1917 г. России.
Но самое удивительное, что премия возобновилась. В 1927 г. ее получил Г. Вейль, а в 1937 г. Э. Картан и советский геометр В.В. Вагнер. И снова началась война, и снова перерыв. В 1950 г. премию Н.И. Лобачевского учредила Академия наук СССР. Ее удостоились А.Д. Александров, А.В. Погорелов, Л.С. Понтрягин, Х. Хопф, П.С. Александров, Б.Н. Делоне, С.П. Новиков, Г. Буземан, А.Н. Колмогоров, В.И. Арнольд и Г.А. Маргулис.
Очень хочется верить в то, что этот список не прервется и будет продолжен именами новых математиков, действительно, на вечные времена!
Пожалуй, самая известная из международных премий, которыми награждаются математики, — это премия Филдса. Ее учредитель Джон Чарлз Филдс родился в 1863 г. в Канаде, окончил университет в Торонто, потом долго жил в Европе, но вернулся в Торонто и работал там до конца жизни. Его научные работы связаны с теорией алгебраических функций и алгеброй. Однако больше всего Филдс был известен как общественный деятель. Именно благодаря его активности в 1924 г. состоялся Международный математический конгресс в Торонто. На этом конгрессе обсуждалась идея Филдса — учредить международную премию и медаль по математике. Филдс писал: «Я особо подчеркиваю, что медаль должна быть интернациональна и объективна, насколько это возможно....Она ни под каким видом не должна включать упоминание о какой-либо стране, институте или личности».
Впервые эта награда была вручена на международном конгрессе в Осло в 1936 г. С тех пор на каждом международном конгрессе ее присуждают самым выдающимся математикам. На медали выгравированы только фамилия лауреата и год присуждения премии. Там нет никакого упоминания о Филдсе. И тем не менее и премию, и медаль называют его именем. Часто медаль Филдса называют «математическим Нобелем».
Филдс считал, что премия должна не только отмечать уже достигнутые успехи, но стимулировать творческую деятельность лауреата. Современники Филдса истолковали эту фразу как указание на то, что награждать следует относительно молодых ученых. Чуть позже установилась возрастная граница: лауреат должен быть не старше 40 лет. И число номинантов этой премии – 4 человека.
В 2006 г. состоялось событие, всколыхнувшее не только весь научный математический мир, но и всю общественность Планеты. На состоявшемся в Мадриде Международном математическом конгрессе были объявлены имена номинантов премии Филдса. Победителями стали австралиец Теренс Тао, француз Венделин Вернер, а также россияне Андрей Окунков и Григорий Перельман. За все существование этой премии ее получили 44 математика, среди них 8 россиян.
В связи с этим журнал Science назвал работу петербургского математика Григория Перельмана, доказавшего гипотезу Пуанкаре, главным научным прорывом в 2006 году.
Перельман решил задачу, с которой не справились лучшие умы XX века.
Гипотеза Пуанкаре является центральной проблемой топологии — науки о геометрических свойствах объектов, не меняющихся при малых деформациях. Математики в течение столетия бились над этой проблемой, пока Перельман не опубликовал ее решение в интернете.
Григория Перельмана наградили за доказательство проблемы Пуанкаре, касающейся так называемых трехмерных поверхностей. Проблема Пуанкаре была одной из «задач тысячелетия», за которую американский Институт Клея пообещал премию в размере $1 млн. Однако Григорий Перельман отказался от получения своего миллиона, не пояснив причины своего демарша. Так, по словам американского математика Джона Болла, Григорий Перельман не захотел приехать в Мадрид, поскольку не считает себя частью «международного математического сообщества». «Никакой враждебности по отношению к математикам у него нет и быть не может,— считают его бывшие коллеги по Математическому институту имени Стеклова, где до последнего времени работал господин Перельман.— Его просто не устраивают некоторые нормы жизни и существования науки, как и всех нас».
Кто же он, наш современник, величайший математик века, отказавшийся от таких наград?
Григорий Перельман слывет в научном мире бескорыстным человеком, лишенным всякого честолюбия. Ученый отклонил присуждение ему докторской диссертации, отказался от продвижения по работе. В 1996 году он не явился на церемонию вручения премии, присужденной Европейским конгрессом математиков.
Перельман родился 13 июня 1966 года, и его удивительные способности стали основанием для раннего зачисления в физико-математическую спецшколу Петербурга. В 16 лет он получил золотую медаль с высшими баллами на Международной математической олимпиаде 1982 года для одаренных школьников. Защитив диссертацию в Петербургском государственном университете, он работал в институте математики им. Стеклова, а в конце 1980-х приехал в США, где работал в разных университетах. Примерно 10 лет назад он вернулся в свой институт, чтобы работать над доказательством формы Вселенной.
Математический мир заволновался еще в 2002 году, когда он впервые опубликовал свою новаторскую работу, посвященную задаче, сформулированной французским математиком, физиком и философом Жюлем Анри Пуанкаре в 1904 году. Гипотеза Пуанкаре, которую большинству нематематиков трудно даже понять, занимала величайшие умы XX века.
Еще раз подчеркнем, что она касается геометрии многомерных пространств и является ключом в сферу топологии. Перельман утверждает, что решил задачу в более общем виде, названном гипотезой геометризации Терстона, частным случаем которой является гипотеза Пуанкаре.
Как видите для человека науки, увлеченного идеей, не важны награды. Ему не интересны деньги. Лучшая награда для него — это доказательство его теоремы, что не совсем понятно для многих из нас.
Итак, мы рассмотрели 4 лекцию, завершающую курс математики. Но уже по сложившейся традиции вам необходимо выполнить самостоятельную работу №4, задания 33-40 домашней контрольной работы.
Надеемся, что Вы уже выполнили компьютерный практикум, контрольный компьютерный практикум – настало время выполнять экзаменационное тестирование. Мы желаем вам успехов!
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 792; Нарушение авторских прав?; Мы поможем в написании вашей работы!