Несобственный интеграл

Определенный интеграл

Пример 9. Вычислить интеграл .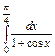

Решение. Для того, чтобы вычислить данный интеграл, воспользуемся основной тригонометрической заменой:

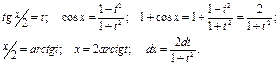
Так как данный интеграл является определенным, то при замене переменной, меняются пределы интегрирования:

.

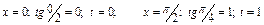На отрезке по переменной t функция 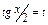непрерывно дифференцируема, монотонна и в границах его принимает значения границ отрезка по переменной x. Следовательно, выбранная замена переменной правомерна. Получаем:

.

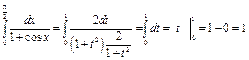Пример 10. Вычислить несобственный интеграл 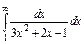или доказать его расходимость.

Решение. Перейдем от несобственного интеграла к определенному с границами 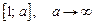. Далее считаем полученный интеграл, с помощью обычных правил интегрирования:

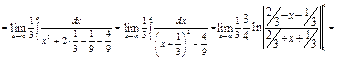
Пример 11. Вычислить несобственный интеграл 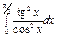или установить его расходимость.

Решение. Так же, как и в предыдущем примере, перейдем от несобственного интеграла к определенному под знаком предела.

.

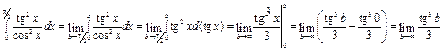Замечание: когда , то .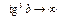

Поэтому получаем, что 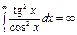, а это значит, что данный интеграл расходится.

Пример 12. Вычислить интеграл от разрывной функции или установить его расходимость.

Решение. Данная подынтегральная функция имеет разрыв в точке х =0, поэтому разделим исходный интеграл на два несобственных интеграла, так как они будут представлять собой интегралы от разрывной функции в точке границы отрезка интегрирования.

. (1)

Так как подынтегральная функция имеет разрыв на правом конце отрезка интегрирования, то:

.

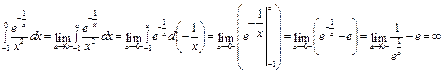Таким образом, на отрезке 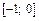интеграл расходится, а следовательно расходится и исходный интеграл, так как равенство (1) справедливо только для сходящихся интегралов в правой части.

Приложения определенного интеграла

1. Площадь плоской криволинейной трапеции.

Пример 13. Вычислить площадь фигуры, ограниченной линиями:

.

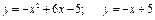Решение. Построим фигуру, площадь которой надо вычислить. Одной из линий является параболой с вершиной в точке С с координатами (3;4). Вторая линия – прямая.

Найдем координаты точек пересечения данных линий:

Для этого решаем систему уравнений 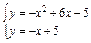, ее решением являются точки A(2;3),B(5;0).

Фигура ACB не является криволинейной трапецией, поэтому для вычисления площади данной фигуры рассмотрим разность площадей двух криволинейных трапеций: FACB и FAB.

Для вычисления площадей воспользуемся формулой:

, где a и b это пределы, в которых изменяется переменная х. В данном случае для обеих фигур a=2, b=5. Из чертежа видно, что для фигуры FACB . Вычислим площадь этой фигуры:

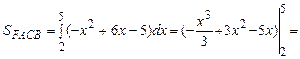
Для фигуры FAB 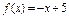, следовательно, имеем:

.

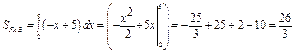Площадь искомой фигуры будет равна: .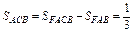

Пример 14. Вычислить площадь фигуры, ограниченной линией .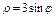

Решение. Построим данную кривую.

Полярные координаты точек кривой получаются заданием значений угла 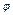и вычислением значений 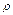из равенства 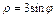. Положение точки А на плоскости в полярной системе координат определяют расстоянием 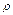от полюса 0 до точки и углом 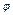, образованным отрезком ОА с полярной осью.

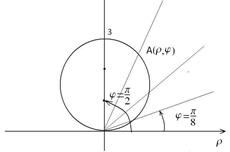
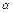Вычислим площадь данной фигуры по формуле: , где и 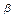пределы, в которых лежит данная фигура. В нашем случае .

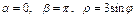Подставляя все эти величины в формулу, получаем:

2. Вычисление длины дуги плоской кривой.

Пример 15. Вычислить длину дуги кривой: , между точками пересечения с осями координат.

Решение. Данная кривая задана в параметрическом виде, то есть x и y зависят от параметра t. Поэтому, чтобы построить точку с координатами (x,y) нужно задать некоторое значение параметра и потом посчитать x и y.

Построим график и найдем точки пересечения с осями координат: .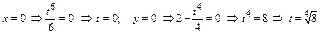

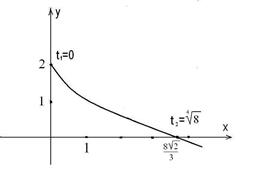
Длина дуги вычисляется по формуле .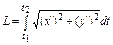

Для данной задачи .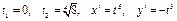

Подставляя все эти значения в формулу, получаем:

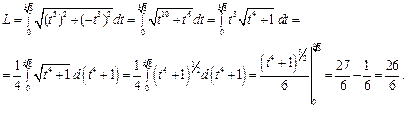
Дата добавления: 2015-06-30