
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила дифференцирования
|
|
|
|
.
Теперь числитель и знаменатель первоначальной дроби можно представить произведением, что помогает вычислить предел
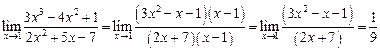 .
.
В третьем примере (в) вычисляется предел при 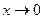 для неопределенности типа
для неопределенности типа 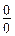 с участием тригонометрических функций. Для выполнения этого задания следует использовать первый замечательный предел или его разновидности
с участием тригонометрических функций. Для выполнения этого задания следует использовать первый замечательный предел или его разновидности
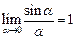 ,
, 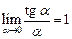 ,
, 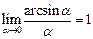 ,
,
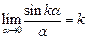 ,
,  .
.
Кроме того нужны некоторые формулы из тригонометрии
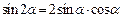 ,
, 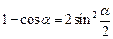 ,
, 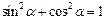 .
.
Пример для задания в):
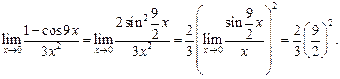
В заданиях (г) требуется раскрыть неопределенность типа 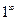 , либо
, либо  . Для их вычисления следует использовать второй замечательный предел
. Для их вычисления следует использовать второй замечательный предел
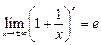 ;
; 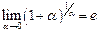
и свойства логарифмов
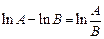 ;
;  .
.
Примеры для задания г):
1 ) 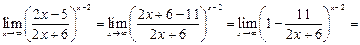
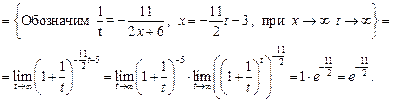
2) 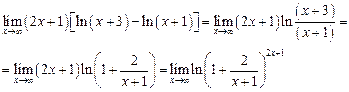
Так как функция 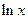 непрерывная, то можно перейти к пределу под знаком функции, т.е.
непрерывная, то можно перейти к пределу под знаком функции, т.е.
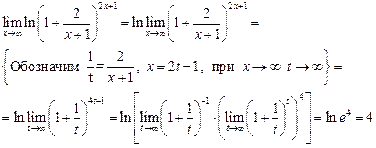
ЗАДАНИЕ 7
Для нахождения производных необходимо знание основных формул дифференцирования.
Пусть 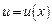 ,
, 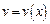 ,
, 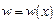 , тогда
, тогда
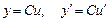 ;
; 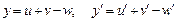 ;
;
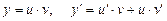 ;
;
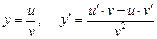 ;
; 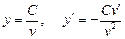 ;
;
Производная сложной функции 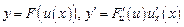 .
.
Таблица производных
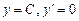 ;
; 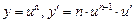 ;
;
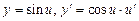 ;
; 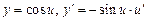 ;
;
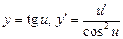 ;
; 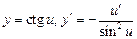 ;
;
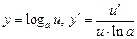 ;
; 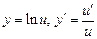 ;
;
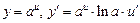 ;
; 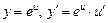 ;
;
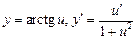 ;
; 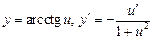 ;
;
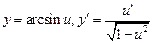 ;
; 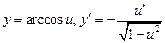 ;
;
формула для логарифмического дифференцирования
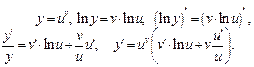 (27)
(27)
Примеры для заданий а) и б):
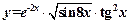 . Находим производную от произведения функций.
. Находим производную от произведения функций.
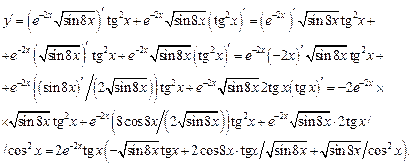
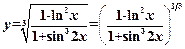 .
.
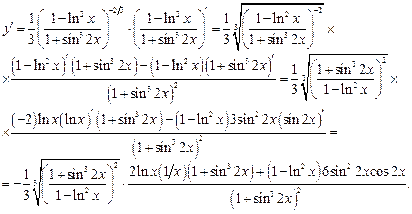
 .
.
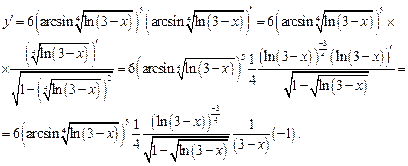
Пример для задания в):
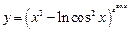 . Используя формулу (27), найдем
. Используя формулу (27), найдем
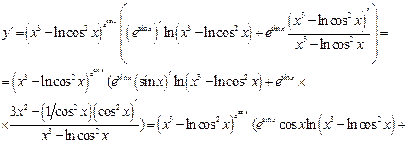
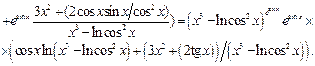
Пример для задания г): 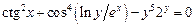 . Переменная
. Переменная 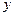 задана как неявная функция. Продифференцируем обе части равенства, считая
задана как неявная функция. Продифференцируем обе части равенства, считая 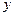 функцией от
функцией от 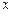 .
.
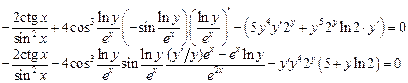
Объединив члены, содержащие 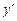
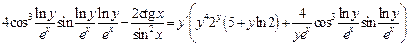
найдем
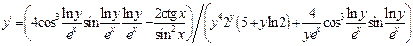
ЗАДАНИЕ 8
Найти первую и вторую производные функции.
Пример. а): 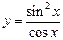 . Найдем первую производную
. Найдем первую производную 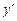 :
:
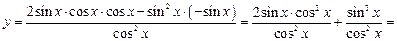
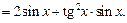 Дифференцируя выражение для
Дифференцируя выражение для 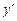 , вычислим вторую производную
, вычислим вторую производную 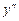 :
: 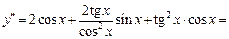
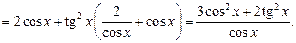
б) 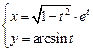 .
.
Функция задана параметрически. Вычислим
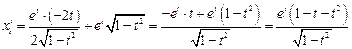 ,
,  . Первая производная
. Первая производная 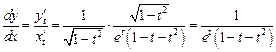 .
.
Вторая производная 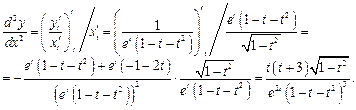
Этот же результат можно получить, если воспользоваться для нахождения второй производной формулой 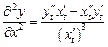 , вычислив
, вычислив 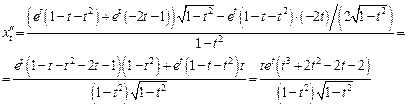 и
и 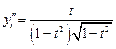 .
.
|
|
|
Задание 9
Исследовать функцию и построить ее график.
Пример. Рассмотрим функцию 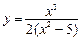 .
.
1. Данная функция существует при всех значениях кроме точек, где знаменатель обращается в ноль 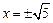 . Поэтому областью определения функции являются все действительные числа, кроме чисел
. Поэтому областью определения функции являются все действительные числа, кроме чисел 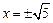 , а именно:
, а именно:
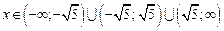 .
.
2. Данная функция 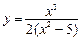 является нечетной, так как
является нечетной, так как 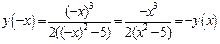 . Функция непериодическая.
. Функция непериодическая.
3. Найдем интервалы возрастания и убывания функции, точки экстремума. Для этого вычислим первую производную
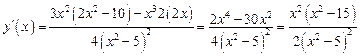 . (28)
. (28)
Используем необходимый признак экстремума: если функция имеет экстремум в некоторой точке, то первая производная в этой точке либо равна нулю, либо не существует. Из (28) найдем, что первая производная равна нулю при 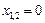 и
и 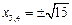 ; не существует при
; не существует при 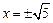 , но последние два значения не входят в область определения функции. Точки
, но последние два значения не входят в область определения функции. Точки 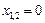 и
и 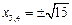 разбивают область определения функции на интервалы
разбивают область определения функции на интервалы
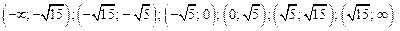 .
.
Чтобы определить, возрастает или убывает функция на каждом из перечисленных интервалов, воспользуемся достаточным признаком возрастания (убывания) функции.
Найдем знак первой производной в каждом из интервалов. Для этого возьмем любое значение переменой 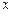 из соответственного интервала и, подставим его в выражение для
из соответственного интервала и, подставим его в выражение для 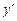 и определим знак первой производной при выбранном значении
и определим знак первой производной при выбранном значении 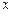 . Так, в интервале
. Так, в интервале 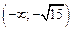
 , значит, функция на этом интервале возрастает. В интервале
, значит, функция на этом интервале возрастает. В интервале 
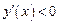 , т. е. функция на этом интервале убывает и т. д.
, т. е. функция на этом интервале убывает и т. д.
Результаты исследования записаны в таблице 1. Здесь же даны выводы о том, является ли критическая точка экстремальной или нет при помощи достаточного признака экстремума функции в критической точке по 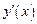 . Из таблицы 1 видно, что при
. Из таблицы 1 видно, что при  функция достигает максимума (
функция достигает максимума (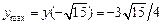 ). Точка
). Точка 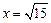 является точкой минимума (
является точкой минимума (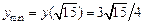 ), так как при переходе через эту критическую точку производная
), так как при переходе через эту критическую точку производная 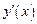 меняет знак с «–» на «+».
меняет знак с «–» на «+».
Таблица 1
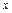
| 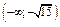
| 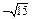
| 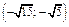
| 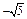
| 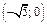
| |
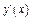
| + | - | Не сущ. | - | ||
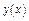
| 
| 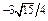 max
max
| 
| Не сущ. | 
|
Продолжение таблицы 1
|
|
|
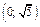
| 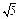
| 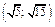
| 
| 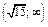
|
| - | Не сущ. | - | + | |

| Не сущ. | 
| 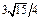 min min
| 
|
4. Вычисляя 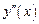 , найдем интервалы выпуклости, вогнутости и точки перегиба (таблица 2).
, найдем интервалы выпуклости, вогнутости и точки перегиба (таблица 2).
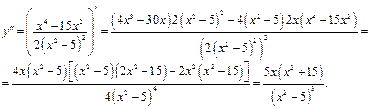
Отсюда имеем 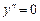 при
при 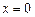 , а при
, а при 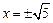
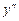 не существует. Так как при
не существует. Так как при 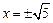 и функция не существует, то стационарной точкой для второй производной является только
и функция не существует, то стационарной точкой для второй производной является только 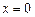 . Эта точка разбивает область определения функции на промежутки
. Эта точка разбивает область определения функции на промежутки
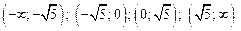 .
.
Таблица 2
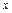
| 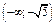
| 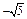
| 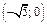
| 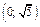
| 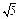
| 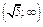
| |
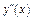
| - | Не сущ. | + | - | Не сущ. | + | |
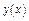
| 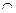
| Не сущ. | 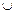
| 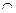
| Не сущ. | 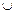
|
Отсюда видно, что начало координат О (0; 0) – точка перегиба графика.
5. Найдем асимптоты графика функции:
а) Вертикальные асимптоты.
Так как в данном случае функция имеет вид дроби, то из условия обращения в ноль знаменателя найдем вертикальные асимптоты: 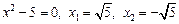 . Так как
. Так как 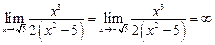 , то по определению прямые
, то по определению прямые  и
и 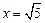 являются вертикальными асимптотами.
являются вертикальными асимптотами.
б) Наклонные асимптоты (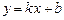 ).
).
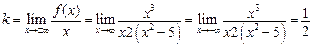 ;
;
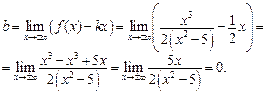
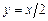 – наклонная асимптота графика функции.
– наклонная асимптота графика функции.
6. Точкой пересечения графика функции с осями координат будет точка О(0;0), так как при 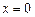 имеем
имеем 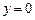 .
.
Таким образом, функция возрастает на интервалах 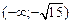 и
и 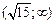 , убывает на интервалах
, убывает на интервалах 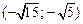 ,
, 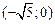 ,
, 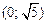 ,
, 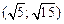 является выпуклой при
является выпуклой при 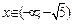 ,
, 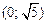 и вогнута при
и вогнута при 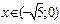 и
и 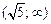 .
.
Строим график функции (рисунок 1), отметив вначале на плоскости 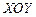 асимптоты графика функции
асимптоты графика функции 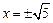 ,
, 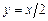 ; точки экстремума функции
; точки экстремума функции 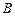 (
(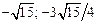 ) и
) и 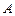 (
( ), точку перегиба О(0;0).
), точку перегиба О(0;0).

Рис. 1 Чертеж к заданию 4.
Задание 10
Найти частные производные второго порядка функции 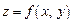 .
.
Частной производной по 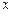 от функции
от функции 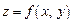 называется предел
называется предел 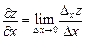 ; аналогично
; аналогично  ,
,
где 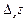 и
и 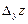 - соответственные частные приращения.
- соответственные частные приращения.
При вычислении частных производных используют следующее правило: частная производная по 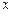 от
от 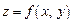 равна производной от
равна производной от 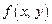 , вычисленной в предположении, что только
, вычисленной в предположении, что только 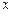 является переменной, а
является переменной, а 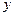 формально считается постоянной. Аналогично вычисляется и частная производная по
формально считается постоянной. Аналогично вычисляется и частная производная по 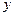 .
.
Пример. Дана функция 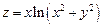 . Найдем производные первого порядка
. Найдем производные первого порядка 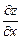 и
и 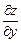 . Считая
. Считая 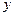 постоянной, получим
постоянной, получим 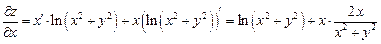 .
.
Считая 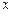 постоянной, вычислим
постоянной, вычислим 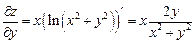 .
.
Подобным образом найдем производные второго порядка:
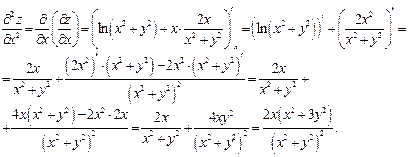
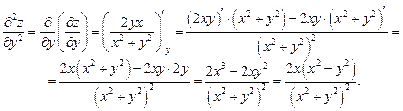
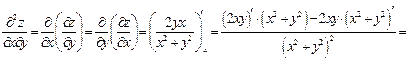
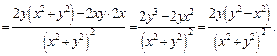
Задание 11
Пусть задана функция трех переменных 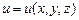 . В трехмерном пространстве
. В трехмерном пространстве 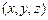 существуют точки, в которых функция
существуют точки, в которых функция 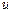 принимает одинаковое значение, которое обозначим через
принимает одинаковое значение, которое обозначим через 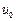 :
:
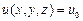 . (29)
. (29)
С геометрической точки зрения (29) – уравнение некоторой поверхности, которую принято называть поверхностью уровня. Если величину 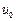 изменять, то из (29) будем иметь семейство поверхностей уровня. Пусть функция
изменять, то из (29) будем иметь семейство поверхностей уровня. Пусть функция 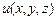 однозначная. Тогда две различные поверхности уровня не будут пересекаться. Поверхности уровня обладают и еще одним свойством, для чего надо ввести понятие вектора – градиента:
однозначная. Тогда две различные поверхности уровня не будут пересекаться. Поверхности уровня обладают и еще одним свойством, для чего надо ввести понятие вектора – градиента:
|
|
|
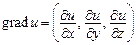 . (30)
. (30)
Оказывается, вектор 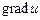 , вычисленный в точке поверхности уровня, всегда направлен по нормали к этой поверхности.
, вычисленный в точке поверхности уровня, всегда направлен по нормали к этой поверхности.
Вектор 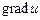 удобно использовать при вычислении производной от некоторой функции
удобно использовать при вычислении производной от некоторой функции 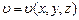 по заданному направлению вдоль единичного вектора
по заданному направлению вдоль единичного вектора 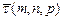 , где
, где 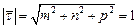 .
.
Формула для вычисления производной по заданному направлению имеет вид скалярного произведения единичного вектора 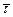 на вектор
на вектор 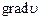 , вычисленного в некоторой точке
, вычисленного в некоторой точке 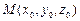 , координаты которой должны быть заданы:
, координаты которой должны быть заданы:
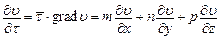 . (31)
. (31)
Пример. Вычислить производную функции 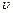 в точке
в точке 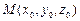 по направлению вектора
по направлению вектора 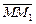 .
.
Пусть 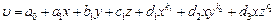 (32)
(32)
Возьмем 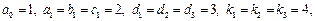
 .
.
а) Найдем координаты вектора 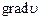 в точке М. Для этого:
в точке М. Для этого:
1) Запишем конкретный вид для 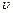 :
:
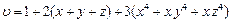 .
.
2) Вычислим частные производные
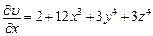 ;
; 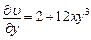 ;
; 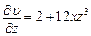 .
.
3) В точке 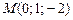 они принимают значения
они принимают значения
 ;
; 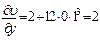 ;
;  .
.
Поэтому вектор 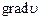 в данной точке
в данной точке  имеет вид
имеет вид
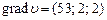 . (33)
. (33)
б) Найдем единичный вектор 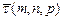 , имеющей направление
, имеющей направление  .
.
1) Вектор  имеет координаты
имеет координаты 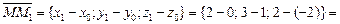
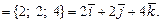
2) Длина вектора  определяется по формуле
определяется по формуле 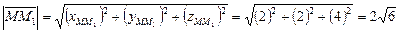 .
.
3) Единичный вектор 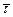 вдоль вектора
вдоль вектора  найдем по формуле
найдем по формуле 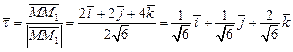 .
.
Откуда 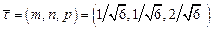 . (34)
. (34)
После подстановки вектора 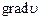 из (33) и значений m, n, p из (34) в формулу (31) получим значение для искомой производной по заданному направлению
из (33) и значений m, n, p из (34) в формулу (31) получим значение для искомой производной по заданному направлению
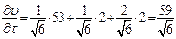 .
.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М., Наука, 1984 (Дрофа, 2006)
2. Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Линейная алгебра в вопросах и задачах. М., Наука, Физматлит, 2001.
3. Воеводин В.В. Линейная алгебра. М., Наука, 1980 (Лань, 2008)
4. Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. М., Наука, Физматлит, 2000.
5. Ильин В.А., Позняк Э.Г. Аналитическая геометрия: Учебник для вузов. М. Физматлит, 2007.
6. Ильин В.А., Позняк Э.Г. Линейная алгебра: Учебник для вузов. М. Физматлит, 2007.
7. Краснов М.Л., Киселев А.И., Макаренко Г.И. Шикин Е.В., Заляпин В.И. Вся высшая математика: Учебник. Т.1 – Т.6. Издательство УРСС, 2002.
|
|
|
8. Кудрявцев Л.Д. Краткий курс математического анализа. т. 1, 2. Альфа, 1998 (Физматлит, 2005).
9. Шипачев В.С. Высшая математика. М. Высш. школа. 2002.
10. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1.: М. Высш. школа. 1996.
Учебное издание
учебное Пособие
ДЛЯ выполнения КОНТРОЛЬНОЙ РАБОТЫ № 1
ПО МАТЕМАТИКЕ
Для студентов всех направлений
квалификация (степень) «бакалавр», «специалист»
заочной формы обучения
Составители: Сайко Дмитрий Сергеевич
Чернышов Александр Данилович
Минаева Надежда Витальевна
Кузнецов Сергей Фёдорович
Ковалёва Елена Николаевна
Половинкина Марина Васильевна
Никифорова Ольга Юрьевна
Соболева Елена Александровна
Подписано в печать 01.2014. Формат 60 х 84 1/16.
Усл. печ. л. 1,5. Тираж 150 экз. Заказ.С – 28.
ФГБОУ ВПО «Воронежский государственный университет
инженерных технологий» (ФГБОУ ВПО «вгуит»)
Отдел оперативной полиграфии ФГБОУ ВПО «вгуит»
Адрес университета и отдела оперативной полиграфии:
394036 Воронеж, пр. Революции, 19.
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 441; Нарушение авторских прав?; Мы поможем в написании вашей работы!