Метод резолюций

Метод семантических таблиц

Методы доказательства – это алгоритмические процедуры, посредством которых можно установить, является ли данное высказывание тавтологией. Первый из описанных методов алгоритмического доказательства использует семантические таблицы. Генцен в 1934 году доказал, что все тавтологии могут быть получены применением некоторых правил, а Бет и Хинтикка в 1955 году построили алгоритм, проверяющий, является ли данное выражение тавтологией или нет.

Основой для построения семантических таблиц является атомарная семантическая таблица, которая строится на основе законов исчисления высказываний.

¯ ¯

¯

¯	¯	¯	¯ ¯
¯ ¯	¯ ¯	¯ ¯ ¯ ¯	¯ ¯ ¯ ¯

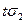
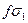
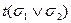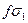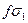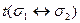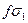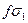Пусть – высказывание. Обозначим через - утверждение “ истинно”, а через - утверждение “ ложно”. При этом – и называются помеченными формулами.

Вершинами семантической таблицы называются все помеченные формулы, встречающиеся в таблице. Вершина семантической таблицы называется особой, если она встречается как корень некоторой атомарной семантической таблицы. В противном случае вершина называется обычной. Ветвь семантической таблицы называется противоречивой, если для некоторого высказывания помеченные формулы и являются вершинами этой ветви. Семантическая таблица называется

замкнутой, если каждая непротиворечивая ее ветвь не содержит обычных вершин. В противном случае семантическая таблица называется незамкнутой.

Семантическая таблица противоречива, если каждая ее ветвь противоречива. Алгоритм построения семантической таблицы для выражения :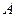

Помещаем помеченную формулу 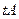или 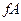в корень.

Шаг . Пусть мы уже построили семантическую таблицу , .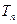

Шаг 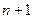. Расширим семантическую таблицу 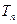до семантической таблицы 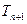. При этом мы пользуемся некоторой вершиной семантической таблицы 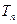, которую в дальнейшем не будем использовать. Из всех обычных вершин 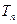, ближайших к корню, выбираем самую левую. Обозначим выбранную вершину .

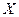К концу каждой непротиворечивой ветви семантической таблицы 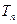мы присоединяем атомарную семантическую таблицу, имеющую корнем 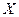. (При этом вершина 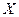становится особой вершиной.) В результате получаем семантическую таблицу 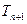(как правило, мы не записываем саму вершину 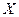, так как она уже присутствует в каждой из рассматриваемых непротиворечивых ветвей).

Построение заканчивается, если каждая непротиворечивая ветвь не содержит обычных вершин.

Доказательством или выводом по Бету высказывания 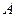называется замкнутая противоречивая семантическая таблица, в корне которой помещена помеченная формула 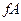. Замкнутая противоречивая таблица, имеющая в качестве корня 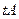, называется опровержением по Бету высказывания .

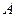Итак, если замкнутая семантическая таблица с 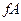в корне противоречива (что означает, что мы всеми возможными способами пытались сделать высказывание 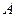ложным и не сумели), то 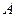- тавтология.

Если не все ветви семантической таблицы противоречивы, то это свидетельствует о том, при некоторой комбинации значений атомов, входящих в исходное выражение, это выражение будет истинным, а при другой комбинации - ложным.

Построим семантическую таблицу для выражения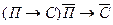

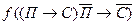
½

½

½

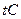
½

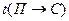
½

½

½ ½

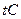
Рис. 3.1. Непротиворечивая семантическая таблица

В построенной семантической таблице (рис.3.1.) нет противоречивых ветвей, что свидетельствует о том, что не при какой комбинации значений атомов данное выражение не будет истинным.

Докажем методом семантических таблиц, что выражение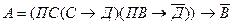

является тавтологией.

Помещаем в корень семантической таблицы 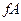, а затем, пользуясь атомарной семантической таблицей, раскроем последовательно функцию импликации, функцию отрицания, функцию конъюнкции и, наконец, оставшиеся функции импликации (рис. 3.2.).

Все ветви построенной семантической таблицы являются противоречивыми, следовательно, предположение о ложности рассматриваемого выражения является неверным, следовательно, данное выражение есть – тавтология.

½

|

|

½

½

½

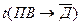
½

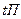
½

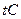
½ ½

Å | |

| | |

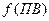
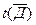
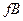
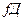
Å Å Å

Рис. 3.2. Пример противоречивой семантической таблицы

В качестве примера приведём ещё две семантические таблицы

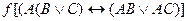
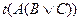
½ ½

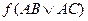
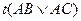
½ ½

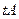
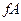
½ ½ ½

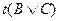
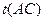
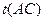
½ ½ ½ ½ ½

½ ½ ½ ½ ½

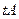
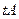
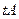
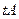
½ ½ ½ ½ ½

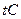
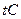
½ ½ Å Å ½ ½

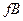
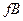
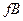
Ž ½ ½ ½

Ž ½ Å Å

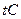
ÅÅ

Рис. 3.3. Пример противоречивой семантической таблицы

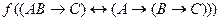
½ ½

½ ½

½ ½

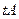
½ ½

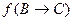
½

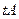
½ ½

½ ½ ½ ½

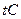
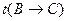
½ ½ Å Å ½ ½

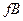
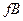
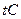
Å Å Å Å

Рис. 3.4. Пример противоречивой семантической таблицы

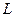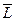Пропозициональные символы с отрицанием либо без отрицания, входящую в элементарную сумму (дизъюнкт), называют литералами (литерами) логики высказываний. Литеры и называют контрарными.

Резольвентой двух дизъюнктов 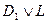и 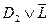называется дизъюнкт .

Теорема. Резольвента является логическим следствием порождающих ее дизъюнктов, то есть, ╞ .

Докажем эту теорему. =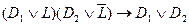

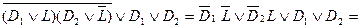
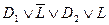= =1.

Метод резолюций доказательства невыполнимости формулы 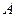состоит в том, что эта формула представляется в КНФ и к ней конъюнктивно присоединяются все возможные резольвенты ее дизъюнктов и получаемых в процессе доказательства резольвент. Полнота метода резолюций состоит в том, что он гарантирует получение для формулы 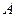следствия false, если 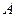невыполнима. Если же, перебрав все возможные резольвенты формулы 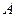, мы не нашли пустую резольвенту, то 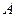не является невыполнимой.

Вывод пустого дизъюнкта может быть наглядно представлен с помощью дерева вывода, вершинами которого являются или исходные дизъюнкты, или резольвенты, а корнем – пустой дизъюнкт.

Пусть задано множество дизъюнктов . Для заданного множества дизъюнктов дерево поиска представлено на рис. 3.5.

Пример 1. Доказать правильность логического вывода.

Если я пойду завтра на первое занятие, то должен буду встать рано, а если я пойду вечером на танцы, то лягу спать поздно. Если я лягу спать поздно, а встану рано, то вынужден довольствоваться пятью часами сна. Я просто не в состоянии обойтись пятью часами сна. Вывод: я должен или пропустить завтра первое занятие, или не ходить на танцы.

Введем следующие обозначения:

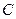- “Я пойду на первое занятие”;

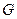- “Я должен встать рано”;

- “Я пойду на танцы”;

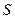- “Я лягу спать поздно”;

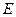- “Я могу обойтись пятью часами сна”.

Рис.3.5. Дерево поиска

Данной задаче соответствует следующее формальное описание: ; ; ╞ .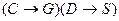

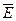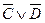Так как доказательство проводится методом от противного, то вывод берется с отрицанием. Исходные посылки и вывод, взятый с отрицанием, представим в виде множества дизъюнктов и будем формировать возможные резольвенты с целью получения нулевой резольвенты.

1. ;

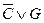2. ;

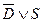3. ;

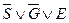4. ;

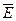5. C;

6. D;

7. 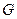(1,5);

8. 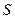(2,6);

9. 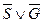(3,4);

10. 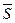(7,9).

11. Нулевая резольвента () (8,10).

Получение нулевой резольвенты свидетельствует о невыполнимости исходной формулы, то есть, мы пытались всеми возможными методами подтвердить ложность вывода, но нам это не удалось. Следовательно, вывод является правильным.

Как следует из этого примера, формирование резольвент не является однозначной процедурой.

Существует много различных подходов к реализации метода резолюций, которые позволяют формализовать этот процесс.

Дата добавления: 2015-06-27