Решение. 1.1. В нашей задаче необходимо определить месячные объемы выпуска продукции вида А и Б

1.1. В нашей задаче необходимо определить месячные объемы выпуска продукции вида А и Б. Обозначим эти объемы как переменные модели:

х₁ – месячный объем выпуска продукции А,

х₂ – месячный объем выпуска продукции Б.

Используя данные таблицы, получим:

расход сырья = 4х1 +х2,

затраты времени работы оборудования = 1х1 + 3х2,

затраты рабочего времени = 8х1 + 1х2.

Так как ежемесячный расход ресурсов не может превышать их максимально возможный месячный размер, то имеем ограничения

4х1 + х2 £ 423

1х1 + 3х2 £ 245

8х1 + 1х2 £ 442

Еще одно неявное ограничение состоит в том, что переменные х₁ и х₂ должны быть неотрицательны, т.е. х₁ ³0, х₂³0.

Целевая функция модели должна выражать основную цель деятельности предприятия. В нашем примере это получение максимальной выручки от реализации произведенной в течении месяца продукции. Если обозначить функцию размера выручки через Z, то

Z = 146х₁ + 208х₂,

а основная цель предприятия может быть выражена так:

Максимизировать целевую функцию Z= 146х₁ + 208х₂,

Перепишем это условие в следующей форме: Z = 146х₁ + 208х₂® max.

Таким образом, математическая модель оптимизации выпуска продукции может быть записана в следующем виде.

Найти неизвестные значения переменных х₁ и х₂, удовлетворяющие ограничениям

4х1 + х2 £ 423

1х1 + 3х2 £ 245

8х1 + 1х2 £ 442

х₁ ³0, х₂³0

и доставляющих максимальное значение целевой функции Z = 146х₁ + 208х₂® max.

Построенная модель является задачей линейного программирования. Любое решение, удовлетворяющее ограничениям модели, называется допустимым, а допустимое решение, доставляющее максимальное значение целевой функции, называется оптимальным.

1.2. Решение задачи линейного программирования с двумя переменными может быть получено графическим способом.

Построим множество допустимых решений или область допустимых решений. Проводим перпендикулярные оси координат: горизонтальная – ось Ох₁, вертикальная - Ох₂. Условия неотрицательности переменных х₁ ³0, х₂³0 показывают, что область допустимых решений будет лежать в первом квадранте системы координат. Для изображения на плоскости множества точек, координаты которых удовлетворяют оставшимся ограничениям модели, рассмотрим уравнения, получаемые из неравенств модели заменой знака «£» на знак «=». В результате такой замены получим три линейных уравнения прямых:

4х1 + х2 = 423	(1)
1х1 + 3х2 = 245	(2)
8х1 + 1х2 = 442	(3)
х1 ³0, х2³0

Для того, чтобы провести на плоскости прямую линию, достаточно знать любые две различные точки, лежащие на этой прямой. Рассмотрим уравнение первой прямой. Если положить х₁ = 0, то х₂ =186, а при х₂ = 0, х₁ = 111,6. Следовательно, прямая (1) проходит через точки с координатами (0;186) и (111,6;0). Обозначим эту прямую как линия (1).

Прямая (2) проходит через точки с координатами (0;148,5) и (118,8;0).

Прямая (3) проходит через точки с координатами (0;111) и (222;0).

Каждая прямая делит плоскость на две полуплоскости. Точки расположенные по одну сторону прямой, удовлетворяют соответствующему неравенству, а точки, расположенные по другую сторону, не удовлетворяют. Для того, чтобы определить искомую полуплоскость, выбирается некоторая «тестовая» точка и ее координаты подставляются в левую часть неравенства. Если для этой точки неравенство выполняется, то она лежит в искомой полуплоскости, т.е. все точки этой полуплоскости удовлетворяют неравенству модели. Если же для «тестовой» точки неравенство не выполняется, то искомой будет та полуплоскость, которая не содержит эту точку. Взяв в качестве «тестовой» точку с координатами (0;0), убеждаемся, что она удовлетворяет всем неравенствам модели.

Следовательно, все полуплоскости, соответствующие неравенствам модели, содержат точку (0,0).

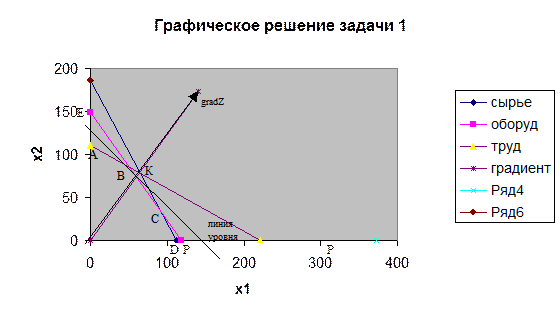
Точки множества допустимых решений должны удовлетворять всем ограничениям. Следовательно, множество допустимых решений является пересечением всех допустимых полуплоскостей и представляет собой многоугольник АВСDО. Любая точка, расположенная внутри этого многоугольника или на любом отрезке его границы, является допустимым решением, т.е. удовлетворяет всем ограничениям модели.

Для нахождения оптимального решения задачи необходимо определить направление возрастания целевой функции.

Вектор, компоненты которого являются коэффициентами целевой функции при переменных х₁ и х₂, называют вектором – градиентом целевой функции и обозначают grad Z.

Целевая функция может возрастать до тех пор, пока линии уровня соответствующие возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и линии уровня, соответствующей максимально возможному значению целевой функции, и будет точкой максимума.

На рисунке видно, что оптимальное решение соответствует точке В, лежащей на пересечении прямых (2) и (3). Поэтому ее координаты находим как решение системы линейных уравнений, задающих эти прямые:

1х1 + 3х2 = 245

8х1 + 1х2 = 442

Решая эту систему находим х₁* = 50, х₂*= 86. При этом значение целевой функции Z = 146х₁* + 208х₂* = 146 ´ 50+ 208´ 86 = 65820

Полученное решение означает, что предприятию необходимо ежемесячно производить 50 единиц продукции А и 86 единиц продукции Б, что позволит ему получать максимальную месячную выручку в размере 65820 рублей.

1.3. Найти неизвестные значения переменных u_1, u₂, u₃, удовлетворяющих ограничениям:

4u1 + 1u2 + 8u3 ³ 146

1u1 + 3u2 + 1u3 ³ 208

u₁ ³0, u₂ ³0, u₃ ³ 0  

и доставляющих минимальное значение целевой функции

W = 423u₁ + 245u₂ + 442u₃ ® min.

Для рассматриваемой нами задачи условия «дополнительной нежесткости» имеют вид:

u₁ (423 - 4x₁- 1x₂ )= 0 x₁(4u1 + 1u2 + 8u3 - 146)= 0

u₂(245 - 1x₁ – 3x₂)= 0 x₂(1u1 + 3u2 + 1u3 - 208) = 0

u₃(442 - 8x₁ – 1x₂)= 0

u₁ ³0, u₂ ³0, u₃ ³ 0,

Подставляя в них найденные значения х₁* = 50, х₂*= 86, получим:

так как х₁* = 50, то 4u1 + 1u2 + 8u3 - 146 = 0

так как х₂* = 86, то 1u1 + 3u2 + 1u3 - 208 = 0

так как 423 -5х₁* – 3 х₂* =423 – 5´50 -3´86 = 50 ¹0, то u₁^* = 0.

Получаем систему уравнений:

4u1 + 1u2 + 8u3 - 146 = 0

1u1 + 3u2 + 1u3 - 208 = 0

u₁=0

Решая эту систему, находим оптимальные значения переменных двойственной задачи:

u₁* = 0, u₂* = 54, u₃* = 76

Вычислим оптимальное значение целевой функции двойственной задачи:

W = 423 × 0 + 245 × 54 + 442 × 76 = 65820, т.е. Z* = W* = 65820, что соответствует первой теореме двойственности.

Для исследуемой задачи оптимизации производственной программы получим

u₁ – стоимостная оценка сырья, ее размерность [руб./1 кг сырья];

u₂ – стоимостная оценка времени работы оборудования, ее размерность [руб./1 ст.час];

u₃ – стоимостная оценка трудовых ресурсов, [руб./1 чел.-час];

u₁* = 0 означает, что ни увеличение, ни уменьшение месячного количества сырья не приведет к изменению оптимального значения суммарной выручки.

u₂* = 54 означает, что при изменении количества оборудования с 54 стан.-час до 54 + Δm, изменение максимальной суммарной выручки составит u₂* Δm (руб.) = 54Δm (руб).

u₃* = 76 означает, при изменении месячного размера трудоресурсов с 76 стан.-час до 76 + Δt, изменение максимальной суммарной выручки составит u₃* Δt (руб.) = 76Δt (руб).

Задача 3

Малое предприятие намерено организовать в следующем квартале выпуск продукции А и Б, пользующейся высоким спросом на рынке. Предприятие располагает необходимым сырьем и оборудованием и может привлечь квалифицированных рабочих на условиях почасовой оплаты, но не имеет средств на оплату труда рабочих. Для этого оно может получить в банке кредит сроком на три месяца под 40% годовых с погашением кредита и процентов по нему в конце квартала.

Информация о нормах затрат сырья, оборудования и трудовых ресурсов, объемах сырья и парка оборудования, имеющихся в распоряжении предприятия, размер выручки от реализации продукции А и Б приведены в таблице:

Наименование ресурсов	Норма затрат на	Объем ресурса
Продукт А	Продукт В
Сырье (кг)
Оборудование (ст.час.)
Трудоресурсы(чел.час.)			?
Цена реализации (руб.)

Целью организации выпуска новой продукции является получение максимальной суммарной прибыли, которая определяется как разность между суммарной выручкой, полученной от реализации произведенной за квартал продукции А и Б, и затратами, связанными с обеспечением кредита (возврат суммы кредита и начисленных процентов).

Требуется:

1. Построить математическую модель оптимизации выпуска продукции с использованием кредита для выплаты зарплаты рабочими с произвольной почасовой ставкой t (руб./чел.-час) оплаты труда.

2. Определить оптимальную программу выпуска продукции, максимальную прибыль, необходимый размер кредита, сумму уплаченных процентов и потребность в трудовых ресурсах, если почасовая ставка t оплаты труда равна 10 руб./чел.-час.

3. Найти функцию спроса на трудовые ресурсы, как функцию почасовой ставки оплаты труда t, построить график этой функции. Исследовать зависимость размеров максимальной прибыли и кредита, обеспечивающего ее получение, от почасовой ставки t оплаты труда в диапазоне от 10 до 60 рублей за чел.-час. Найти функции, выражающие эти зависимости, и построить их графики.

Дата добавления: 2015-06-27