
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методом Фурье
|
|
|
|
Решение краевой задачи для уравнения теплопроводности
В соответствии с методом разделения переменных, ищем решение уравнения 29) в виде произведения двух функций: 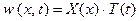 . Тогда подстановка
. Тогда подстановка 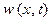 в таком виде в уравнение 29), даст
в таком виде в уравнение 29), даст 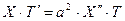 или
или 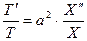 .
.
Приравниваем левую и правую часть последнего соотношения константе
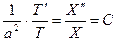 .
.
Последние соотношения распадаются на два самостоятельных обыкновенных дифференциальных уравнения
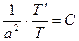 и
и 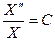
или
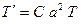 и
и 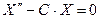 . 33)
. 33)
Первое уравнение из 33) – обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Его решение
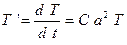
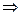
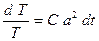
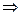
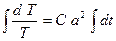
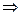
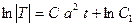
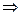
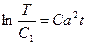
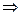
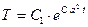 .
.
Поскольку ни в одном сечении стержня температура 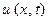 , а, следовательно, и функция
, а, следовательно, и функция 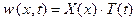 не может неограниченно возрастать по абсолютной величине при
не может неограниченно возрастать по абсолютной величине при 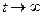 , то
, то 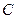 должно быть отрицательным. Обозначим
должно быть отрицательным. Обозначим 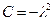 . Тогда
. Тогда 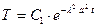 .
.
Второе уравнение из 33) теперь имеет вид 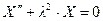 . Это - однородное линейное уравнение второго порядка с постоянными коэффициентами. Его решение, строящееся по виду корней характеристического уравнения:
. Это - однородное линейное уравнение второго порядка с постоянными коэффициентами. Его решение, строящееся по виду корней характеристического уравнения: 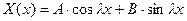 .
.
Теперь решение задачи с однородными граничными условиями имеет вид 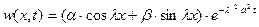 , 34)
, 34)
где 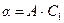 ,
, 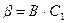 - произвольные постоянные (неопределенные коэффициенты).
- произвольные постоянные (неопределенные коэффициенты).
Реализуя в 34) граничные условия 31), получим
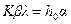 ,
,
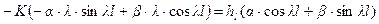 ,
,
из этих соотношений имеем
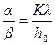 и
и 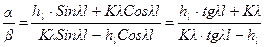
откуда

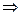
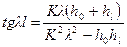 .
.
Таким образом, успешность решения сформулированной краевой задачи 29), 31), 32) зависит от успешности решения последнего трансцендентного уравнения относительно неизвестной величины 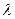 .
.
Рассмотрим дальнейшее решение поставленной задачи на следующем примере. Пусть исходная краевая задача, состоящая из дифференциального уравнения 24) и начального условия 25), имеет граничные условия такие, что левый конец теплоизолирован, а правый поддерживается при постоянной температуре:
|
|
|
 ,
, 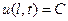 . 35)
. 35)
Граничные условия 35) неоднородны и замена 28) приводит к следующей краевой задаче относительно введенной дополнительной функции 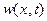 :
:
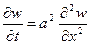 ,
,
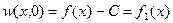 , 36)
, 36)
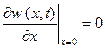 ,
, 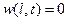 .
.
Введенные константы 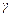 и
и 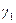 определяются из системы
определяются из системы 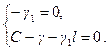
И равны 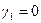 и
и 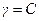 .
.
Решение методом разделения переменных дифференциального уравнения в 36) приводит к соотношению:
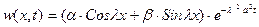 .
.
Реализация в последнем соотношении граничных условий из 36) дает
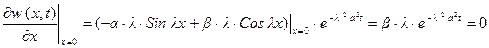
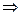
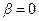 ,
,
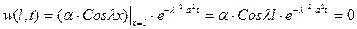
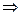
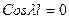
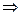
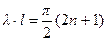 ,
, 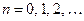
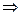
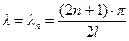 - собственные числа решаемой задачи, функции
- собственные числа решаемой задачи, функции 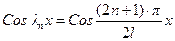 - собственные функции.
- собственные функции.
Теперь частные решения 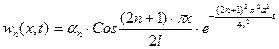 .
.
Общее решение
 . 37)
. 37)
Коэффициенты 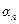 определяются из начального условия
определяются из начального условия 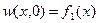 , а тогда
, а тогда 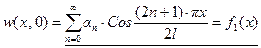 . Подчеркнутое выражение представляет разложение заданной функции
. Подчеркнутое выражение представляет разложение заданной функции 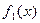 в ряд Фурье по косинусам на интервале
в ряд Фурье по косинусам на интервале 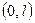 , коэффициенты этого разложения
, коэффициенты этого разложения 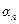 - коэффициенты Фурье, которые определяются по формулам:
- коэффициенты Фурье, которые определяются по формулам:
 . 38)
. 38)
Таким образом, сформулированная краевая задача 36) имеет решение 37), где коэффициенты 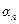 определяются по формулам 38).
определяются по формулам 38).
Если начальная температура стержня постоянна 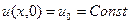 , то
, то 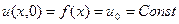 и
и 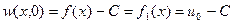 , а тогда
, а тогда 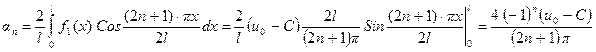 и теперь искомое решение имеет вид:
и теперь искомое решение имеет вид:
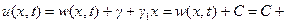
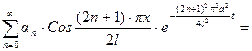
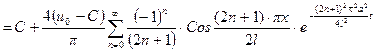 .
.
Для качественного анализа полученного результата, ограничимся в ряде разложения для 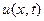 одним членом ряда, тогда
одним членом ряда, тогда
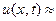
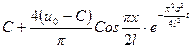 .
.
На рис. 3 приводится характер изменения температуры в стержне с ростом времени (кривые 1, 2, 3). Кривая 3 здесь соответствует более позднему моменту времени, чем кривые 1 и 2. Здесь принято 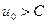 .
.
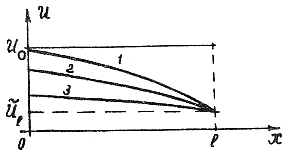
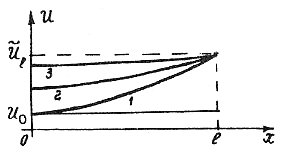
Рис. 3 Рис. 4
Если 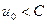 , то характер изменения температуры с ростом времени представлен на рис. 4. Кривая 3 здесь так же соответствует более позднему моменту времени, чем кривые 1 и 2. Таким образом, в нашем случае, когда стержень теплоизолирован с боков и со стороны левого торца, а правый то-рец поддерживается при постоянной температуре, температура в стержне с течением времени стремится сравняться с температурой правого торца.
, то характер изменения температуры с ростом времени представлен на рис. 4. Кривая 3 здесь так же соответствует более позднему моменту времени, чем кривые 1 и 2. Таким образом, в нашем случае, когда стержень теплоизолирован с боков и со стороны левого торца, а правый то-рец поддерживается при постоянной температуре, температура в стержне с течением времени стремится сравняться с температурой правого торца.
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 517; Нарушение авторских прав?; Мы поможем в написании вашей работы!