Теплопроводности методом конечных разностей

Решение первой краевой задачи для уравнения

Первая краевая задача для уравнения теплопроводности формулируется следующим образом. Требуется найти решение уравнения теплопроводности 3), удовлетворяющее краевым условиям:

, ;

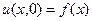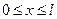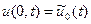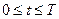, ; 39)

, .

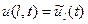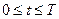Таким образом, требуется найти решение 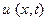в прямоугольнике, ограниченном прямыми , , 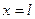, , 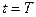если заданы значения искомой функции на трех сторонах прямоугольника , , .

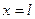Одним из наиболее простых приближенных методов решения этой краевой задачи является сведение ее к системе конечно-разностных (сеточных) уравнений. Для этого покроем область решения сеткой, образованной прямыми 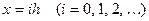, , 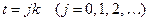и будем определять приближенные значения решения в узлах сетки, то есть в точках пересечения этих прямых. Введем обозначения 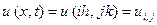. На основании теоремы о конечных приращениях Лагранжа, заменим производные соответствующими разностями:

,

,

.

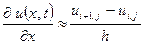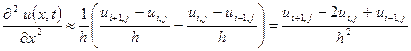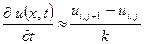Теперь вместо дифференциального уравнения 24) имеем соответствующее ему уравнение в конечных разностях для точки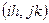

.

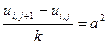
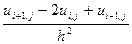Определим из этого соотношения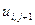

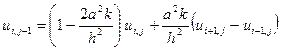. 40)

Из последней формулы видно, что по трем известным значениям искомой функции в j- том горизонтальном ряду 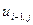, , 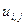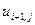определяется значение 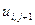в i -ом горизонтальном ряду. Нам известны все значения температуры на прямой 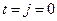(из начального условия). По формуле 40) определяются значения температуры во всех внутренних точках отрезка 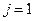(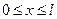). Значения в крайних точках этого отрезка нам известны из граничных условий 39). Так ряд за рядом определяются значения искомого решения во всех узлах сетки.

Формула 40) упрощается, если шаг 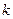по оси 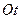выбрать так, чтобы было 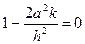, тогда 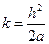и соотношение 40) принимает вид: 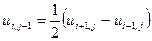. Последняя формула особенно удобна для вычислений. Доказывается, что 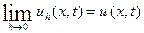, где 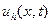- приближенное решение, полученное по последней формуле, 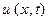- точное решение задачи.

Дата добавления: 2015-07-13