
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системи лінійно незалежних функцій
|
|
|
|
Означення. Функції y  ,…,y
,…,y  називаються лінійно залежними на множині Х, якщо існує набір чисел α
називаються лінійно залежними на множині Х, якщо існує набір чисел α  …α
…α  , не всі з яких дорівнюють нулю, таких, що α
, не всі з яких дорівнюють нулю, таких, що α 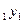 +…+α
+…+α 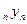 ≡0 для будь-яких х є Х.
≡0 для будь-яких х є Х.
Якщо це визначення не виконується, то функції y  ,…,y
,…,y  називаються лінійно незалежними.
називаються лінійно незалежними.
Приклад (лінійно незалежних). Функції 1,х,...,х  на [a;b] лінійно незалежні. Якщо допустити, що вони залежні, то
на [a;b] лінійно незалежні. Якщо допустити, що вони залежні, то  (не всі рівні 0) такі, що α
(не всі рівні 0) такі, що α  +α
+α 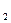 х…+α
х…+α  х
х 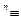 0 для всіх х є [a;b], а це протиріччя основної теореми алгебри. Значить функції 1,х,...,х
0 для всіх х є [a;b], а це протиріччя основної теореми алгебри. Значить функції 1,х,...,х  на [a;b] лінійно незалежні.
на [a;b] лінійно незалежні.
Теорема. Нехай дана система лінійно залежних функцій y  ,…,y
,…,y  на множині Х. Тоді визначник Вронского:
на множині Х. Тоді визначник Вронского:

 на множині Х.
на множині Х.
Доведення. Оскільки y  ,…,y
,…,y  лінійно залежні то існує набір α
лінійно залежні то існує набір α  …α
…α  , не всі з яких дорівнюють нулю, для яких виконується тотожність
, не всі з яких дорівнюють нулю, для яких виконується тотожність  , тоді y
, тоді y  ,…,y
,…,y  задовольняють системі
задовольняють системі
 , для будь-якого х є Х.
, для будь-якого х є Х.
Система відносно (α  …α
…α  ) має не тривіальне рішення для будь-якого х є Х. Таким чином, з курсу алгебри маємо, що W(х)=0,
) має не тривіальне рішення для будь-якого х є Х. Таким чином, з курсу алгебри маємо, що W(х)=0,  х є Х.
х є Х.
Теорема. Нехай y  ,…,y
,…,y  –лінійно незалежна система рішень однорідного лінійного рівняння y
–лінійно незалежна система рішень однорідного лінійного рівняння y 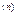 +p
+p  (x)y
(x)y 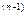 +…+p
+…+p  (x)y=0 такого, що
(x)y=0 такого, що  – визначені і неперервні на [a;b]. Тоді для будь-якого х є [a;b] визначник Вронского відмінний від нуля W(х)
– визначені і неперервні на [a;b]. Тоді для будь-якого х є [a;b] визначник Вронского відмінний від нуля W(х)  0.
0.
Доведення. Припустимо противне, що в деякій точці x 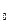 є[a;b] W(х
є[a;b] W(х 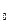 )=0. Візьмемо функцію у=
)=0. Візьмемо функцію у=  , де α
, де α  …α
…α  –довільні константи, тоді у - рішення даного рівняння.
–довільні константи, тоді у - рішення даного рівняння.
Розглянемо систему:

Для даної системи W(х 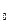 )=0, виходить, система має нетривіальне рішення, тобто існує набір α
)=0, виходить, система має нетривіальне рішення, тобто існує набір α  …α
…α  , для якого не всі α
, для якого не всі α  дорівнюють нулю і такий, що задовольняє системі. Розглянемо у, коли в якості (α
дорівнюють нулю і такий, що задовольняє системі. Розглянемо у, коли в якості (α  …α
…α  ) узято указане нетривіальне рішення системи, тоді маємо
) узято указане нетривіальне рішення системи, тоді маємо
 .
.
Таким чином, у=  є нетривіальним рішенням рівняння з нульовими початковими умовами у точці
є нетривіальним рішенням рівняння з нульовими початковими умовами у точці  . Зазначимо, що функція у
. Зазначимо, що функція у  0 задовольняє нульовим початковим умовам і рівнянню. Оскільки коефіцієнти рівняння задовольняють теоремі про існування та єдиності рішення, то у=
0 задовольняє нульовим початковим умовам і рівнянню. Оскільки коефіцієнти рівняння задовольняють теоремі про існування та єдиності рішення, то у= 
 , що протирічить лінійній незалежності
, що протирічить лінійній незалежності 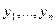 таким чином наше припущення не вірно, тобто W(х)
таким чином наше припущення не вірно, тобто W(х)  0 для будь-якого х є [a;b].
0 для будь-якого х є [a;b].
|
|
|
Теорема. Нехай дане лінійне однорідне рівняння: y 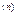 +p
+p  (x) y
(x) y 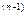 +…+p
+…+p  (x)y=0, де p
(x)y=0, де p  …p
…p  –визначені і неперервні на [ a;b ],
–визначені і неперервні на [ a;b ], 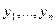 –лінійно незалежна система рішень даного рівняння, тоді у=с
–лінійно незалежна система рішень даного рівняння, тоді у=с 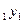 +…+с
+…+с 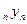 , де с
, де с 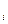
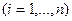 – довільні константи, є загальним рішенням даного рівняння.
– довільні константи, є загальним рішенням даного рівняння.
Доведення. Зразу відмітимо, що згідно властивостей рішень лінійного однорідного рівняння у=с 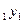 +…+с
+…+с 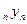 - рішення рівняння. Покажемо, що рішення будь-якої задачі Коші для даного рівняння можна отримати з рішення у=с
- рішення рівняння. Покажемо, що рішення будь-якої задачі Коші для даного рівняння можна отримати з рішення у=с 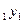 +…+с
+…+с 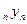 , якщо взяти відповідні значення с
, якщо взяти відповідні значення с 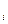
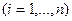 . Нехай в будь-якій точці
. Нехай в будь-якій точці  є[a;b] задані довільні початкові умови
є[a;b] задані довільні початкові умови
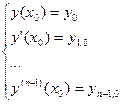 .
.
Підставляючи замість у його значення, отримаємо

Визначник даної системи є визначник Вронского і W(  )
)  0, в силу попередньої теореми, отже система має нетривіальне рішення, підставляючи яке в у одержимо шукане рішення задачі.
0, в силу попередньої теореми, отже система має нетривіальне рішення, підставляючи яке в у одержимо шукане рішення задачі.
Наслідок. Лінійне однорідне рівняння n-го порядку має n-лінійно незалежних рішень.
Означення. Будь-який набір з n-лінійно незалежних рішень лінійного однорідного рівняння називається фундаментальною системою рішень.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 349; Нарушение авторских прав?; Мы поможем в написании вашей работы!