
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Постановка крайової задачі
|
|
|
|
Лекція №11. Рівняння гіперболічного типу. Постановка крайової задачі. Теорема єдиності розв’язку
Рівняння коливання струни, стержня, мембрани, а також гідродинаміки і акустики, в загальному вигляді має вид
 .
.
Як і в випадку звичайних рівнянь, воно має безкінечне число розв’язків. Тому, у випадку реального фізичного процесу, для єдиності розв’язку, що характеризує процес, необхідні додаткові умови. Ці умови складаються з граничних і початкових умов.
Розглянемо ситуацію на прикладі коливання струни. Так процес коливання струни залежить від її початкової форми і розподілу швидкостей, тобто початкові умови слід задавати у вигляді:
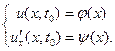
Що до граничних умов, то можна говорити про три основні типи:
1. гранична умова першого роду  (задано режим);
(задано режим);
2. гранична умова другого роду  (задано силу);
(задано силу);
3. гранична умова третього роду  (пружне закріплення).
(пружне закріплення).
Аналогічно задається гранична умова і на другому кінці  .
.
Комбінуючи різні граничні умови ми отримаємо 6 типів крайових задач.
Сформулюємо першу крайову задачу для гіперболічних рівнянь:
Знайти 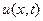 , визначену в області
, визначену в області 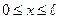 ,
, 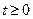 , що задовольняє рівняння
, що задовольняє рівняння
 для
для 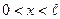 ,
, 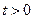 ;
;
граничним умовам:

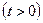
 ;
;
і початковим умовам:

 ,
,  .
.
Якщо на обох кінцях береться гранична умова другого або третього роду, то відповідна задача називається другою або третьою крайовою задачею. У випадку коли граничні умови при х=0 і х=  мають різні типи, крайова задача називається мішаною.
мають різні типи, крайова задача називається мішаною.
При умові, що вплив граничних умов в точці 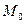 , розміщеної достатньо далеко від кінців, буде мати місце через великий проміжок часу, а ми розглядаємо явище в продовж малого проміжку, то задачу можна розглядати як граничну задачу лише з початковими умовами.
, розміщеної достатньо далеко від кінців, буде мати місце через великий проміжок часу, а ми розглядаємо явище в продовж малого проміжку, то задачу можна розглядати як граничну задачу лише з початковими умовами.
|
|
|
Знайти розв’язок рівняння  з початковими умовами
з початковими умовами
 .
.
Цю задачу називають задачею Коши.
Якщо явище розглядається поблизу однієї границі і вплив граничної умови на другій границі не сутьтево то ми приходимо до задачі на напівпрямій  , коли треба знайти розв’язок рівняння задовольняючого умовам
, коли треба знайти розв’язок рівняння задовольняючого умовам
 .
.
Нарешті, коли характер явища, для моментів часу, достатньо віддалених від початкового моменту  , визначається граничними умовами, (так як вплив начальних умов, завдяки тертю, слабшає) то такі ситуації приводять до задачі без початкових умов, тобто:
, визначається граничними умовами, (так як вплив начальних умов, завдяки тертю, слабшає) то такі ситуації приводять до задачі без початкових умов, тобто:
знайти розв’язок 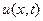 для
для 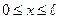 і
і 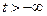 при граничних умовах
при граничних умовах
 .
.
2. Теорема єдиності розв’язку.
При розв’язанні крайових задач:
1. треба переконатись в єдиності розв’язання – це досягається доведенням теореми єдиності;
2. треба переконатись в існуванні розв’язку, що зазвичай зв’язано з методом знаходження розв’язків.
Розглянемо теорему єдиності.
Теорема. Можливе існування тільки однієї функції 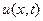 визначеної на області
визначеної на області  , що задовільняє рівнянню
, що задовільняє рівнянню

 ,
,
початковим і граничним умовам
 ,
,
якщо виконуються наступні умови:
1. функція 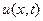 та похідні, що входять в рівняння, а також похідна
та похідні, що входять в рівняння, а також похідна  неперервні на проміжку
неперервні на проміжку 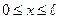 при
при 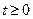 ;
;
2. 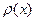 і
і  - неперервні на проміжку
- неперервні на проміжку 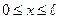 .
.
Доведення. Припустимо що існує два розв’язка  і
і  , тоді
, тоді  задовольняє однорідному рівнянню
задовольняє однорідному рівнянню
 ,
,
однорідним умовам

та умовоі 1 теореми.
Покажемо, що 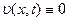 . Розглянемо функцію
. Розглянемо функцію
 (повна енергія струни в момент часу t).
(повна енергія струни в момент часу t).

Інтегруючи частинами перший доданок правої частини, отримаємо
 .
.
Враховуючи граничні і початкові умови на  отримаємо
отримаємо
 (оскільки
(оскільки  задовольняє однорідному рівнянню), тобто
задовольняє однорідному рівнянню), тобто 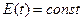 .
.
Враховуючи початкові умови отримаємо
 , так як
, так як  .
.
Користуючись додатністю  і
і  заключаємо що
заключаємо що  і
і  звідки і витікає тотожність
звідки і витікає тотожність  , але
, але  , тобто
, тобто 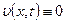 .
.
Таким чином  .
.
Зауваження. Доведення теореми єдиності другої і третьої крайових задач практично не відрізняється від приведеного, що стосується теореми єдиності для задачі Коши і задач без початкових умов то доведення їх можна знайти к книзі [5].
|
|
|
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 383; Нарушение авторских прав?; Мы поможем в написании вашей работы!