
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Постановка крайових задач
|
|
|
|
Лекція №17. Рівняння еліптичного типу
Приклад.
Найпростіша класична теорія охолодження Землі приводить до рівняння
 ,
,  ,
,
 - температура плавлення гірських порід,
- температура плавлення гірських порід,
 - температура поверхні.
- температура поверхні.
Розв’язок
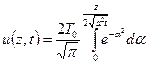
Градієнт функції при  дорівнює
дорівнює
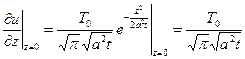
Підставляючи сюди відомі значення геотермічного градієнту

 - коефіцієнт температуропровідності базальтів і гранітів отримаємо для тривалості процесу охолодження значення
- коефіцієнт температуропровідності базальтів і гранітів отримаємо для тривалості процесу охолодження значення  років.
років.
З відкриттям радіоактивного розпаду схема змінилась, рівняння прийняло вид
 ,
,  , де
, де
А – щільність теплових джерел. При цьому  отримуємо рівним у 2 мільярди років. Дивіться більш докладніше [5].
отримуємо рівним у 2 мільярди років. Дивіться більш докладніше [5].
Розглянемо стаціонарне теплове поле. Розподіл температури буде задовольняти рівнянню (враховуючи, що  )
)  або
або  (рівняння Лапласа)
(рівняння Лапласа)
Задача про стаціонарний розподіл тепла  всередині тіла Т формулюється наступним чином:
всередині тіла Т формулюється наступним чином:
Знайти функцію  що задовольняє всередині Т рівняння
що задовольняє всередині Т рівняння  і граничній умові, одного з наступних видів:
і граничній умові, одного з наступних видів:
1. 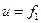 на поверхні
на поверхні  (перша крайова задача),
(перша крайова задача),
2.  на
на 
 - похідна у напрямку нормалі п до поверхні
- похідна у напрямку нормалі п до поверхні  (друга крайова задача),
(друга крайова задача),
3.  на
на  (третя крайова задача).
(третя крайова задача).
Першу крайову задачу називають задачею Дирихлє, а другу – задачею Неймана.
Крім того, якщо розв’язок шукається в внутрішній (в зовнішній) по відношенню до  частини, то відповідно задачу називають внутрішньою (зовнішньою) крайовою задачею.
частини, то відповідно задачу називають внутрішньою (зовнішньою) крайовою задачею.
Розглянемо задачу на площині, тобто для двох змінних. Відмітимо, що функції  і
і  (двох змінних), для яких виконується умова Коші-Рімана
(двох змінних), для яких виконується умова Коші-Рімана 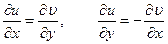 (що називаються гармонійними) будуть задовольняти однорідному рівнянню.
(що називаються гармонійними) будуть задовольняти однорідному рівнянню.
Гармонійна функція, задовольняє принципу міні-максимуму (див. теорію аналітичних функцій), таким чином для першої крайової задачі буде виконуватись теорема єдиності, як це ми доводили раніше.
|
|
|
2. Перша крайова задача для круга. Інтеграл Пуассона.
Розглянемо задачу.
Знайти функцію 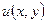 , що задовольняє рівнянню
, що задовольняє рівнянню  всередині (або за межами) круга і граничній умові
всередині (або за межами) круга і граничній умові  на границі круга радіуса a.
на границі круга радіуса a.
Переходячи до полярної систему координат 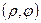 з початком у центрі кола отримаємо рівняння, в полярних координатах у вигляді
з початком у центрі кола отримаємо рівняння, в полярних координатах у вигляді
 .
.
Розв’язок шукається методом розділенням змінних  .
.
Підставляючи до рівняння отримаємо 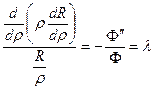 або
або
 .
.
Звідси  . Враховуючи періодичність і
. Враховуючи періодичність і 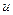
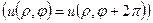 ,
,  - періодична, а це можливо тільки якщо
- періодична, а це можливо тільки якщо  , тобто
, тобто  .
.
Функцію  розшукують у вигляді
розшукують у вигляді 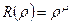 . Підставляючи в рівняння і скорочуючи на
. Підставляючи в рівняння і скорочуючи на  , знайдемо
, знайдемо  або
або 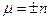 . Отже
. Отже 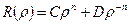
Розв’язок: для  (внутрішня задача) мають вигляд
(внутрішня задача) мають вигляд 
(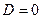 , так як при
, так як при  функція
функція  необмежена і не буде гармонійною), і
необмежена і не буде гармонійною), і  для
для  (зовнішня задача) (
(зовнішня задача) ( , так як при
, так як при 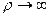 функція
функція  необмежена).
необмежена).
Звідси  (внутрішня задача)
(внутрішня задача)
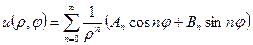 (зовнішня задача).
(зовнішня задача).
Для визначення  і
і  користуються граничними умовами
користуються граничними умовами  .
.
Остаточно будемо мати  (внутрішня задача)
(внутрішня задача)

Для зовнішньої задачі  .
.
Отримані формули можна спростити. Для внутрішньої задачі розглянемо більш детально ситуацію. 

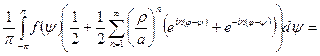
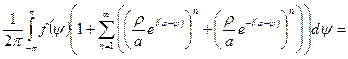


 .
.
Для зовнішньої задачі отримаємо 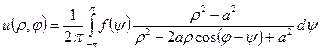 .
.
Отримані інтеграли називаються інтегралами Пуассона.
Відзначимо, що інтеграл Пуассона дає розв’язок крайової задачі для кусочно неперервної функції  (дивіться [5]).
(дивіться [5]).
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 274; Нарушение авторских прав?; Мы поможем в написании вашей работы!