Метод простых итераций 1 страница

Для реализации процесса последовательных приближений для метода простых итераций в EXCEL можно использовать описанную ниже структуру таблицы (рассматривается пример системы:

с решением х₁=3, х₂=-1, х₃=4.)

	A	B	C	D
	Коэффициенты	исходной	системы
			-1
		-1
	х1	х2	х3
	=D2/A2	=D3/B3	=D4/C4
	=($D$2-$B$2*B6-$C$2*C6)/$A$2	=($D$3-$A$3*A6-$C$3*C6)/$B$3	=($D$4-$A$4*A6-$B$4*B6)/$C$4
8…	… копируются формулы из строки 7 на несколько строк вниз

Строки 1-5 содержат текстовые заголовки и числовые значения. В частности, диапазон A2:D4 содержит значения коэффициентов системы. Эти ячейки заполняются вручную.

Также вручную в ячейки A6:C7 заносятся формулы. Они соответствуют формулам (11,12) из конспекта лекций. Затем ячейки A7:C7 выделяются и копируются вниз на несколько строк. Окончание итерационного процесса определяется визуально по совпадению значений двух последовательных приближений (в соседних строках таблицы).

2. Применение модуля "Поиск решения"

"Поиск решения" – модуль EXCEL, применяемый для решения задач с несколькими переменными, поиска одного из нескольких корней алгебраических уравнений и вообще для решения задач, в которых на искомое решение наложены условия в виде уравнений или неравенств.

Модуль "Поиск решения" вызывается через меню: "Сервис" – "Поиск решения". После этого на экране появляется диалоговое окно, с помощью которого осуществляется решение задачи. Структуру и принцип работы с этим окном разберем на примере решения той же системы.

Поиск решения проведем на новом листе рабочей книги. Прежде всего туда копируются исходные коэффициенты, которые вместе с заголовками заполняют диапазон А1:D4. Затем в ячейку А6 вставляется заголовок ' Решение '; оно будет находиться в ячейках А7:А9. В качестве первого приближения в эти ячейки можно занести, например, значения правых частей уравнений. Ячейки Е2:Е4 заполняются формулами для вычисления левых частей уравнений системы. Для этого формула вносится в ячейку Е2 и затем копируется в две другие ячейки. При этом ссылки на ячейки А7:А9 делаются абсолютными (см. ниже структуру получающейся таблицы).

После этого вызывается модуль "Поиск решения". Диалоговое окно имеет вид:

Одна из вспомогательных ячеек, в данном случае Е2, выбирается в качестве целевой и компьютеру дается задание подобрать значения неизвестных так, чтобы значение этой ячейки стало равным значению правой части первого уравнения системы. Для этого переключатель устанавливается на позицию "Значению" и в соответствующее окно ввода заносится численное значение правой части (в данном случае нельзя пользоваться ссылкой на ячейку, содержащую это значение). Два других уравнения образуют набор дополнительных условий, накладываемых на значения переменных. Эти условия заносятся в окно ввода "Ограничения" с помощью диалогового окна, появляющегося после нажатия виртуальной клавиши [Добавить]. Это окно содержит три внутренних окна ввода. В первое вставляется ссылка на ячейку, содержащую формулу вычисления левой части второго уравнения (можно использовать способ быстрого создания ссылок), в третье – ссылка на ячейку, содержащую значение правой части этого уравнения. Второе окно ввода содержит один из знаков математических отношений (равенства или неравенства) и значок раскрывающегося списка. Раскрыв список, можно установить в окне нужный знак – в данном случае знак равенства. Затем так же в окно "Ограничения" вставляется второе условие, т.е., третье уравнение системы. В окно "Изменяя ячейки" вставляются ссылки на ячейки, предназначенные для размещения искомого решения. После выполнения этих подготовительных действий нажимается виртуальная клавиша [Выполнить].

Принцип работы модуля "Поиск решения" ясен из описанной структуры окна. Компьютер подбирает значения неизвестных так, чтобы одновременно соблюдалось и требование (выполнения первого уравнения), и условия (выполнение второго и третьего уравнений). В случае, если ему это удается, в возникающем диалоговом окне появляется сообщение "Решение найдено". Имеющийся в окне переключатель позволяет либо занести в таблицу полученное решение, либо отменить его и восстановить ранее внесенные в ячейки значения.

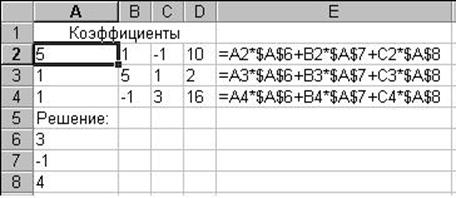Структура таблицы, предназначенной для применения модуля "Поиск решения", в данном случае имеет вид:

Задание: найти решение системы согласно своего варианта методом простых итераций и с помощью модуля "Поиск решения".

Вариант	Aij	bi		Вариант	Aij	bi
	2,5		-0,5	4,8			3,7	3,7	2,7	15,5
		1,5	6,4	-11,36			3,1	-1,5	-4,9	-12,18
	-3,2	2,7	-4	11,36			1,4	6,4	-3,4	-3,4
	3,2	0,8	-1,5	-8,55			5,6	0,9	-1,4	3,24
	0,5	-3,5		-4,9			1,1	0,9	2,2	8,64
	-2,7			20,15			-0,2	3,3	3,7	13,5
	5,3	3,1	1,2	4,13			3,8	2,1	0,5	7,74
	1,2	-6		6,36			0,6	-1,6		11,44
	-0,8	4,2	3,1	0,98			-2		-0,8	-3,2
	-3,2	2,5	-2,3	-1,98			0,25	-1,25	2,75	-1,575
	1,2	-1,3	6,8	13,03			6,6	2,4	-4	-14,42
	3,5	2,8	0,1	-0,14			-4		2,6	12,92

	2,8	6,7	1,6	1,82			1,7	1,1	4,2	7,67
	3,5	0,5	-0,8	2,73			0,6	2,4	1,5	4,32
	0,9		-3,5	-1,59			-3		2,6	-8,38
	2,7		0,5	-7,16			4,8	0,2	3,1	2,9
	3,7	0,8	-1	-2,04			0,6	-2,4	5,2	2,28
	1,2	6,1	-3,8	-32,67			4,4	-2	2,6	1,64
	5,6	0,9	-1,4	16,74			4,7	0,3		5,94
	1,3	0,8	-2	8,3			0,7	2,5	5,2	4,98
	-0,8	3,1	-3,8	11,42			-3	2,1	-4	-3,23
	5,8	1,1	-0,9	13,76			3,7	1,3	0,8	9,81
	1,7	0,5	-2,5	-7,73				2,4	5,1	18,06
	-1,6	3,9	2,4	9,71			-3	0,4	-0,6	-5,22
	0,9	2,5	1,4	14,93			2,2	1,5	2,5	15,65
	1,7	2,4	-2,5	-5,22			4,6	0,8	-2,1	4,9
		-4	3,5	54,4			-1,7	4,4	2,3	14,5
	5,6		1,3	26,64				1,8	3,1	4,7
	1,2	-6,3	2,1	-6,72			-4,2	-0,6	2,4
	-0,8		3,1	7,68			1,6		2,4	-5,3
	2,6	0,8	-0,4	3,5			0,2	1,8	0,4	-0,8
	1,9	1,7	6,4	22,3			-4,4	0,8		-1,76
	-3,4	2,8	-4,2	-11,56			2,8	1,5	2,5	4,04
	2,7	0,9	-0,4	9,87			0,6	2,6	-0,6	4,56
	-1,7	1,6	7,1	55,98				1,2	2,2	7,68
	2,6	2,5	-5	-16,94				2,5	-2,5	11,4
	-3,2	2,5	2,2	4,18
	1,2	1,4	6,8	6,28
	3,5	2,8	0,2	4,74

4.4. Работа 4: Решение задач линейного программирования

В отличие от других работ, при решении задач линейного программирования структура таблицы не является единообразной, но определяется постановкой задачи. Поэтому при выполнении работы студентам следует самостоятельно создать таблицу для решения своей задачи. Рассмотрим пример (т. н. "транспортную задачу").

Условия задачи: Для обеспечения молоком жителей микрорайона города построено четыре мини-завода по его переработке, объемы производства которых соответственно равны 300, 400, 500, 200 тонн. Заключены договора на поставку молока с тремя фермерскими хозяйствами, производственная мощность которых 500, 600, 300 тонн. Затраты на перевозку одной тонны молока от фермерского хозяйства до завода представлены в таблице:

	Заводы
Фермы

Необходимо составить такой план поставок молока, при котором суммарные затраты на транспортировку будут минимальными и заводы будут работать на полную производственную мощность.

Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребности в ней), то в этой задаче не надо учитывать издержки, связанные со складированием и с недопоставками продукции.

Для решения данной задачи построим ее математическую модель. Неизвестными в данной задаче являются объемы перевозок. Пусть x_ij – объем перевозок с i –ой фермы в j –й центр распределения (минизавод). Целевая функция – это суммарные транспортные расходы, т.е.

где с_ij – стоимость перевозки единицы продукции с i –й фермы на j –й центр распределения.

Неизвестные в данной задаче должны удовлетворять следующим ограничениям:

· Объемы перевозок не могут быть отрицательными

· Так как модель сбалансирована, то вся продукция должна быть вывезена с ферм, а потребности всех минизаводов должны быть полностью удовлетворены.

В результате имеем следующую модель:

,

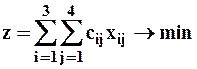при ограничениях:

x_ij 0,

где b_j – спрос на j –м минизаводе, а_i - объем производства на i –й ферме.

Для решения этой задачи с помощью модуля "Поиск решения" введем данные, как это показано на схеме таблицы. В ячейки B2:E4 введены стоимости перевозок. Ячейки B7:E9 отведены под значения неизвестных (объемы перевозок). В ячейки G7:G9 введены объемы производства на фермах, а в ячейки B11:E11 - потребность в молоке на минизаводах. В ячейке F10 находится целевая функция, в диапазоне B10:E10 - формулы, определяющие объем продукции, поставляемой на заводы. В ячейках F7:F9 находятся формулы, вычисляющие объем молока, вывозимого с фермы. Для вычисления целевой функции z использована встроенная функция EXCEL СУММПРОИЗВ, определяющая сумму попарных произведений двух диапазонов одинаковой структуры.

	A	B	C	D	E	F	G
	C =
						a i
						=CУММ(B7:E7)
	X =					=CУММ(B8:E8)
						=CУММ(B9:E9)
	bj	=CУММ (B7:B9)	=CУММ (C7:C9)	=CУММ (D7:D9)	=CУММ (E7:E9)	=СУММПРИЗВ (B2:E4;B7:E9)

В результате таблица будет выглядеть следующим образом:

	A	B	C	D	E	F	G
	C =
						a i
	X =
	bj

Теперь выполним команду меню Сервис, Поиск решения и заполним открывшееся диалоговое окно Поиск решения,как это показано на рисунке.

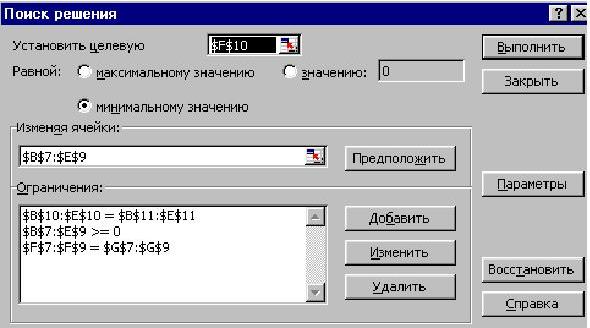Нажатием клавиши [Параметры] следует войти в диалоговое окно "Параметры поиска решения" и установить в нем флажки "Линейная модель" и "Неотрицательные значения". Нажатием кнопки [ОК] производится возврат в окно "Поиск решения".

После нажатия кнопки [Выполнить] подпрограмма поиска решения находит оптимальный план поставок молока и соответствующие ему транспортные расходы. Результаты решения представлены ниже.

	A	B	C	D	E	F	G
	C=
						a i
	X=
	bj

Задание: найти решение задачи линейного программирования, сформулированной в математической форме (то есть, без конкретного смыслового содержания), согласно своего варианта.

1. L = 6x₁ + 5x₂®max 2. L = -x₁ + x₂®max
x₁ + 3x₂ £ 4 2x₁ + 3x₂ ³ 5
2x₁ + x₂ ³ 3 x₂ £ 2
x₁ ³ 0 x₁ + x₂ £ 4
x₂ ³ 0 x₂ ³ 0

3. L = x₁ + x₂®max 4. L = -x₁ + x₂®max
2x₁ + 3x₂ £ 6 x₁ + x₂ £ 3
3x₁ + 2x₂ £ 6 -2x₁ + x₂ ³ 2
x₁ ³ 0, x₂ ³ 0

5. L = x₁ + x₂®min 6. L = x₁ + x₂®min
–2x₁ + x₂ £ 2 x₁ + x₂ ³ 1
-x₁ - x₂ £ 2 x₁ – 2x₂ ³ 0
x₁ ³ 0

7. L = 7x₂®min 8. L = 2x₁ – 3x₂®min
-2,5x₁ + 3x₂ ³ 5 2x₁ - x₂ - x_­ ³ 3
x₁ £ 2 x₁ - x₂ + x₃ ³ 2
x₁ + x₂ £ 6 x_j ³ 0 (j = 1, 2, 3)
x₁ ³ 0

9. L = x₁®min 10. L = 3x₁ + 2x₂®max
-x₁ + x₂ £ 7 2x₁ + x₂ £ 2
x₁ + x₂ = 0 -x₁ + x₂ ³ -3
x₂ ³ 0 -x₁ + x₂ £ 0
x₁ ³ 0, x₂ ³ 0

11. L = 3x₁ + 4x₂®max 12. L = x₁ – 2x₂®max
-x₁ + x₂ £ 1 5x₁ – 2x₂ £ 3
x₁ + x₂ ³ -1 x₁ + x₂ ³ 1
-x₁ + 2x₂ £ 2 -3x₁ + x₂ £ 3
2x₁ - x₂ £ 2 -3x₁ - 3x₂ £ 2
x₁ ³ 0, x₂ ³ 0 x₁ ³ 0, x₂ ³ 0

13. L = 3x₁ + x₂ + 3x₃ + 2x₄®min
5x₁ + x₂ - 3x₃ - 3x₄ ³ 1
–2x₁ + x₂ + x₃ - 3x₄ ³ -2
x₁ ³ 0, x₃ ³ 0, x₄ ³ 0

14. L = 2x₁ - x₂ + 3x₃ + x₄ - x₅®max
x₁ - 2x₂ + x₃ + 3x₄ - 2x₅ £ 4
-x₁ - x₂ + 3x₃ - 2x₄ + 3x₅ £ 10
x_j ³ 0 (j = 1, 2,..., 5)

15. L = 8x₁ + 19x₂ + 7x₃®max 16. L = x₁ + x₂®max
3x₁ + 4x₂ + x₃ £ 1 x₁ + 2x₂ £ 10
x₁ + 3x₂ + 3x₃ £ 2 x₁ + 2x₂ ³ 2
x_j ³ 0 (j = 1, 2, 3) 2x₁ + x₂ £ 10
x₁ ³ 0, x₂ ³ 0

17. L = 2x₁ + 3*x₂®min 18. L = x₁ - x₂®min
x₁ + x₂ £ 4 3х₁ + 2x₂ ³ 6
3x₁ + x₂ ³ 4 x₁ £ 2
x₁ + 5x₂ ³ 4 x₁ + x₂ £ 4
0 £ x₁ £ 3 x₂ ³ 0
0 £ x₂ £ 3

19. L = x₁ + 3x₂ + x₃®max 20. L = x₁ – 2x₂®max
x₁ + x₂ + x₃ = 1 -3x₁ + 2x₂ £ 6
3x₁ - x₂ - x₃ = 1 5x₁ + 2x₂ £ 10
x_j ³ 0 (j = 1, 2, 3) x₁ + x₂ ³ -1
x₁ ³ 0

21. L = x₁ + x₂®min 22. L = 2x₁ + x₂®min
x₁ + x₂ ³ 1 x₁ + x₂ ³ 1
x₁ - 2x₂ £ 1 3x₁ + x₂ £ 4
3x₁ + x₂ ³ 3 2x₁ - x₂ ³ 1
x₁ ³ 0, x₂ ³ 0 x₁ ³ 0, x₂ ³ 0

23. L = x₁ + x₂ + 3x₃®max 24. L = 2x₁ + 3x₂®max
x₁ + 2x₂ + x₃ £ 5 x₁ + x₂ £ 4
2x₁ - x₂ + x₃ ³ 2 2x₁ - x₂ ³ 2
x_j ³ 0 (j = 1, 2, 3) x₂ ³ 0

25. L = 2x₁ – 3x₂®min 26. L = x₁ + 3x₂®max
–4x₁ + 5x₂ £ 20 -x₁ - x₂ ³ -3
2x₁ + x₂ ³ 6 6x₁ + x₂ £ 14
x₁ - x₂ £ 6 2x₁ – 3x₂ £ 6
x₁ ³ 0, x₂ ³ 0 x₁ + x₂ = 4
x₁ ³ 0, x₂ ³ 0

Дата добавления: 2017-01-13