Процессы истечения и дросселирования газов и паров

При решении задач связанных с истечением газа (рис 2.2.) через насадки (сопла) чаще всего приходится определять скорость истечения и расход, т.е. количество газа в единицу времени.

Рис. 2.2. Истечение газа через сопло

Рассмотрение закономерностей движения газов и паров по каналам имеет чрезвычайно большое значение для изучения рабочих процессов ряда машин, аппаратов и устройств (паровые и газовые турбины, эжекторы, реактивные и ракетные двигатели, горелочные устройства и т. п.).

Процессы истечения обычно начинают изучать, принимая следующиедопущения:

а) с течением времени условия движения газа и его параметры неизменяются – стационарная задача;

б) отсутствует теплообмен между потоком газа и внешней средой –адиабатная задача;

в) во всех точках данного поперечного сечения канала скорость ифизические параметры газа одинаковы и изменяются только по длинеканала –одномерная задача.

При указанных допущениях движение газа (пара) удовлетворяетусловиям установившегося движения:

(2.21)

где М – массовый секундный расход газа, кг/с; 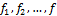– площади поперечных сечений канала, м²; - удельные объемы газа в соответствующих сечениях канала, м³/кг; - скорости истечения в соответствующих сечениях, м/с; P₁, P₂-давление среды на входе и на выходе в сопло соответственно, Па.

В процессах изменения состояния движущегося с конечной скоростью газа теплота расходуется не только на изменение внутренней энергии и на совершение внешней работы (против внешних сил), но и на приращение внешней кинетической энергии газа при его перемещении по каналу. Применительно к потоку газа, движущегося со скоростью W, выражение первого закона термодинамики имеет вид (в дифференциальной форме):

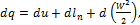(2.22)

где dq – теплота, подводимая к потоку;du – изменение внутренней энергии рабочего тела;dl_n – работа по преодолению внешних сил сопротивления (работа «проталкивания»);d(W²/2) – изменение кинетической энергии 1 кг рабочего тела, движущегося со скоростью W.

Работа проталкивания на единицу массы равна:

=d(pυ). (2.23)

С учетом (2.23) выражение (2.22) можно записать как:

, (2.24)

или:

.

Уравнение (2.24) показывает, что подведенная теплота в процессе при течении газа (или жидкости) расходуется на изменение внутренней энергии, на работу проталкивания и на изменение внешней кинетической энергии рабочего тела или подведенная теплота при течении газа расходуется на изменение его энтальпии и внешней кинетической энергии.

В случае адиабатного истечения через сопло (рис. 2.3) легко найти скорость истечения на выходе (сечение 2), используя выражение (2.24).

Рис. 2.3. Адиабатное истечение через сопло

Скоростью W₁ на входе в сопло обычно пренебрегают:

(2.25)

В формуле (2.25) энтальпия выражена в Дж/кг. Если же она выражена в кДж/кг или в ккал/кг, то формула (2.25) соответственно примет вид (2.26) или (2.27); скорость во всех случаях получается в м/с:

(2.26)

(2.27)

Значения энтальпии определяются по is -диаграмме или по таблицам для данного вещества.

В тех случаях, когда не известна энтальпия рабочего тела, удобнее определять скорость через основные параметры P, υ, T. Формулу дляопределения скорости адиабатного истечения идеального газа легко получить, используя таблицу 2.1 и пренебрегая величинойW₁.

(2.28)

или:

(2.29)

где k и R – соответственно показатель адиабаты и газовая постоянная рабочего тела.

Массовый расход газа определяется из выражения (2.21), которое после подстановки W₂ и некоторых упрощающих преобразований примет вид:

(2.30)

где f₂ – выходное сечение сопла, м²;P₁, υ₁ – соответственно, давление (Па) и удельный объем (м³/кг) на входе в сопло; – отношение давлений в сопле.

Отношение давлений , при котором расход газа становится максимальным, называется критическим и равно

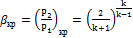. (2.31)

Значения в зависимости от k сведены в таблицу 2.1

Значение критической скорости можно найти по формуле

. (2.32)

Таблица 2.1

Значения k и β_kp при истечении газа

Вид рабочего тела	k	βkp	Вид рабочего тела	k	βkp
Одноатомный идеальный газ	1,67	0,487	Трех- и многоатомные идеальные газы, перегретый пар.	1,29	0,546
Двухатомный идеальный газ	0,40	0,528	Сухой насыщенный пар.	1,135	0,577
Для влажно насыщенного пара k = 1,035+0,1x

При β_кр<β<1 скорость газа и расход растут с уменьшением β. Если уменьшить β в диапазоне от β_кр до 0, то расход не изменяется, оставаясьмаксимальным, а скорость также не изменяется, оставаясь равной W_КР–критической скорости. Итак, при 0<β ≤ β_кр в сужающемся соплеустанавливается критический режим истечения:

М = М_маx, W₂ = W_2кр, P₂ = P_кр = P₁β_кр.

В этом случае М_max и W_2кр надо можно найти по следующим формулам:

, (2.33)

(2.34)

Полное использование возможностей рабочего тела, расширение от P₁ до P₂ при β<β_кр, происходит в комбинированных соплах или соплахЛаваля. Эти каналы имеют сужающуюся и расширяющуюся части. В таких соплах можно получать сверхзвуковые скорости. Если в процессе, изображенном на рис. 2.4, использовать сопло Лаваля, то скорость на выходе из сопла будет:

Рис.2.4. Сопло Лаваля

При прохождении газа или пара через сужение канала (диафрагма, вентиль,клапан и т. п.) происходит снижение его давления без совершениявнешней работы. Этот необратимый процесс называется дросселированием. В большинстве случаев дросселирование, сопровождающееся уменьшением работоспособности тела, приносит безусловный вред. Но иногда оно является необходимым и создается искусственно, например, при регулировании паровых двигателей, в холодильных установках, в приборах, замеряющих расход газа и т. д.При прохождении газа через отверстие, представляющее известное сопротивление, кинетическая энергия газа и его скорость в узком сечении возрастают, что сопровождается падением температуры и давления рис. 2.5)..

Рис. 2.5. Процесс дросселирования

Газ, протекая через отверстие, затрачивает часть кинетической энергии на работу против сил трения, которая превращается в теплоту. В результате температура его изменяется и может, как уменьшаться, так и увеличиваться.

В отверстии скорость газа возрастает. За отверстием, когда газ опять течет по полному сечению, скорость вновь понижается, а давление повышается, но до начального значения оно не доходит; некоторое изменение скорости произойдет в связи с увеличением удельного объема газа от уменьшения давления.

Дросселирование, как указывалось, является необратимым процессом, при котором всегда происходит увеличение энтропии и уменьшение работоспособности рабочего тела. При дросселировании идеального газа его температура не изменяется.

При дросселировании реального газа температура его может уменьшаться, увеличиваться или оставаться неизменной. Если температура реального газа в результате дросселирования остается без изменения, то она называется температурой инверсии Т_инв.

Таким образом, поведение реальных газов при дросселировании существенно отличается от поведения идеальных газов. Изменение температуры реальных газов при дросселировании впервые было обнаружено опытами Джоуля и Томсона и получило название эффекта Джоуля - Томсона.С молекулярной течки зрения эффект Джоуля - Томсона объясняется наличием объема самих молекул и сил сцепления между молекулами реального газа. Влияние объема молекул и сил взаимодействия на изменение температуры в процессе дросселирования различно в зависимости от природы газа и начального состояния реального газа.Задачи, связанные с дросселированием водяного пара, проще всего решаются при помощиi - s – диаграммы.

Дата добавления: 2017-01-14