Циклы паросиловых установок

В тепловых электростанциях в качестве теплового двигателя используются паровые или газовые турбины. В первом случае рабочее тело – водяной пар (реальный газ), во втором – продукты сгорания и углеводородного топлива (идеальный газ).

Тепловыми двигателями называют такие тепловые машины, в которых происходит превращение части подводимой теплоты в полезнуюработу. В непрерывно действующих тепловых машинах происходят замкнутыетермодинамические процессы или циклы, так как рабочее тело требуетсяпериодически возвращать в исходное состояние. Если цикл состоит изобратимых процессов, то такой цикл называется обратимым. Циклыбывают прямыми и обратными. Цикл, в результате которого получается положительная работа, называется прямым циклом, или циклом теплового двигателя; в нем работа расширения больше работы сжатия. Цикл, в результате которого расходуется работа, называется обратным; в нем работа сжатия больше работы расширения. В тепловых двигателях используюттолько прямые циклы.

Из рис. 2.6 следует, что если рабочее тело расширяется по кривой 1-3-2, то оно производит работу, изображаемую на Pυ-диаграмме пл. 13245. По достижении точки 2 рабочее тело должно быть возвращено в начальное состояние (в точку 1), для того чтобы оно снова могло произвести работу. Процесс возвращения тела в начальное состояние может быть осуществлен тремя путями.

1. Кривая сжатия 2-3-1 совпадает с кривой расширения 1-3-2.

В таком процессе вся полученная при расширении работа (пл. 13245) равна работе сжатия (пл. 23154) и положительная работа равна нулю.

2. Кривая сжатия 2-6-1 располагается над линией расширения 1-3-2; при этом на сжатие затрачивается большее количество работы (пл. 51624), чем ее будет получено при расширении (пл. 51324).

3.Кривая сжатия 2-7-1 располагается под линией расширения 1-3-2. В этом круговом процессе работа расширения (пл. 51324) будет больше работы сжатия (пл. 51724). В результате вовне будет отдана положительная работа, изображаемая пл. 13271 внутри замкнутой линии кругового процесса, или цикла.

Повторяя цикл неограниченное число раз, можно за счет подводимой теплоты получить любое количество работы.

Рис. 2.6. Изображение круговых термодинамических процессов на Pυ-диаграмме

Обратимые термодинамические процессы являются идеальными процессами. В них при расширении газ производит максимальную работу, определяемую уравнением:

, (2.35)

где P– давление рабочего тела, равное давлению внешней среды.

А при сжатии, когда рабочее тело возвращается в первоначальное состояние, в обратимом процессе затрачивается минимальная работа.

Все действительные процессы, протекающие в природе и в технике, сопровождаются явлениями трения или теплопроводности при конечной разности температур и являются необратимыми. Однако многие необратимые процессы, с которыми приходится иметь дело на практике, сравнительно мало отличаются от обратимых.

Если хоть один из процессов, входящих в состав цикла, является необратимым, то и весь цикл будет необратимым.

Результаты исследований идеальных циклов могут быть перенесены на действительные, необратимые процессы реальных машин путем введения опытных поправочных коэффициентов.

Термический к.п.д. и холодильный коэффициент циклов

На пути 1-3-2 (см. рис. 2.6) рабочее тело совершает работу расширения l ₁, численно равную пл. 513245, за счет теплоты q₁, полученной от теплоотдатчиков, и частично за счет своей внутренней энергии. На пути 2-7-1 затрачивается работа сжатия l ₂, численно равная пл. 427154, часть которой в виде теплоты q₂ отводится в теплоприемники, а другая часть расходуется на увеличение внутренней энергии рабочего тела до начального состояния. В результате осуществления прямого цикла будет вовне отдана положительная работа, равная разности между работой расширения и сжатия. Эта работа l₀= l₁- l₂.

Так как в цикле конечное состояние тела совпадает с начальным, то изменение внутренней энергии рабочего тела не происходит и равно нулю, поэтому q₁-q₂=q₀= l ₀.

Отношение количества теплоты, превращенной в положительную работу за один цикл, ко всей теплоте, подведенной к рабочему телу, называется термическим коэффициентом полезного действия прямого цикла:

(2.36)

Значение η_t является показателем совершенства цикла теплового двигателя. Чем больше η_t, тем большая часть подведенной теплоты превращается в полезную работу. Величина термического к.п.д. цикла всегда меньше единицы и могла бы быть равна единице, если бы q₁→∞ или q₂ =0, чего осуществить нельзя.

Полученное уравнение (2.36) показывает, что всю подведенную в цикле к рабочему телу теплоту q₁ полностью превратить в работу невозможно без отвода некоторого количества теплоты q₂ в теплоприемник.

Рассмотрим теперь обратный цикл, который проходит в направлении против часовой стрелки и изображается на pυ-диаграмме пл. 13261 (см. рис. 2.6). Расширение рабочего тела в этом цикле совершается при более низкой температуре, чем сжатие, и работа расширения (пл. 132451) получается меньше работы сжатия (пл. 162451). Такой цикл может быть осуществлен только при затрате внешней работы.

В обратном цикле от теплоприемников подводится к рабочему телу теплота q₂ и затрачивается работа l₀, переходящая в равное количество теплоты, которые вместе передаются теплоотдатчикам:

Без затраты работы сам собой такой переход невозможен.

По обратному циклу работают холодильные установки. Степень совершенства обратного цикла определяется так называемым холодильным коэффициентом цикла:

(2.37)

Холодильный коэффициент показывает, какое количество теплоты отнимается от теплоприемника при затрате одной единицы работы. Его величина, как правило, больше единицы.

Прямой обратимый цикл Карно

При осуществлении обратимого произвольного цикла количество источников теплоты может быть уменьшено, если на отдельных участках цикла теплота будет отводиться и подводиться при неизменной температуре, т. е. в изотермных процессах. Предельным случаем будет тот, когда вся теплота в цикле будет подводиться и отводиться в изотермных процессах. В этом предельном случае потребуется всего два источника теплоты постоянной температуры: один теплоотдатчик и один теплоприемник.

В этом цикле, предложенном в 1824 г. С. Карно и носящем его имя, тепло подводится и отводится по изотермам при температурах горячего источника тепла Т₁ и холодного теплоприёмника Т₂.

Диаграмма цикла в Pυ – координатах приведена на рис. 2.7.

Рис. 2.7. Диаграмма прямого цикла Карно вPυ и TS координатах

В этом цикле рабочее тело сначала расширяется изотермически по линии 1-2, получая от горячего источника тепло q₁ при температуре Т₁, затем отключается от горячего источника и продолжает расширяться адиабатно по линии 2-3 с понижением температуры до Т₂.

После этого рабочее тело подключается к холодному теплоприёмнику и сжимается изотермически по линии 3-4, отдавая ему тепло q₂ при температуре Т₂. Затем оно отключается от теплоприёмника и продолжает сжиматься адиабатно по линии 4-1 с повышением температуры до Т₁, чем и завершается цикл.

На рис 2.7 приведён прямой цикл Карно в Тs – диаграмме. Величины энтропии рабочего тела в начале и конце процесса подвода тепла 1-2 соответственно равны s₁ и s₂.

Количество тепла, подводимого в цикле к рабочему телу, равно q₁=T₁∙(s₁-s₂), а количество отводимого тепла q₂=T₂(s₂-s₁).

Согласно определению для термического КПД:

Подставляя в данное уравнение величины q₁ и q₂, получаем уравнение для термического к.п.д. прямого цикла Карно:

(2.38)

Термический к. п. д. обратимого цикла Карно зависит только от абсолютных температур теплоотдатчика и теплоприемника. Он будет тем больше, чем выше температура теплоотдатчика и чем ниже температура теплоприемника. Термический к.п.д. цикла Карно всегда меньше единицы, так как для получения к. п. д., равного единице, необходимо, чтобы Т₂=0 или Т₁=∞, что неосуществимо. Термический КПД цикла Карно не зависит от природы рабочего тела. Термический к. п. д. цикла Карно имеет наибольшее значение по сравнению с к. п. д. любого цикла, осуществляемого в одном и том же интервале температур. Поэтому сравнение термических к. п. д. любого цикла и цикла Карно позволяет делать заключение о степени совершенства использования теплоты в машине, работающей по данному циклу.

В реальных двигателях цикл Карно не осуществляется вследствие практических трудностей. Однако теоретическое и практическое значение цикла Карно весьма велико. Он служит эталоном при оценке совершенства любых циклов тепловых двигателей.

Обратный обратимый цикл Карно

Цикл Карно может протекать не только в прямом, но и в обратном направлении. Цикл Карно. Цикл состоит из обратимых процессов и в целом является обратимым.

υ

Рис. 2.8. Диаграмма обратного обратимого цикла Карно в Pυ координатах

В обратном цикле Карно(рис. 2.8) рабочее тело сначала расширяется адиабатно по линии 1-4 с понижением температуры от Т₁ до Т₂, затем продолжает расширяться изотермически по линии 4-3, получая тепло от холодного источника в количестве q₂ при температуре Т₂. После этого оно сжимается адиабатно по линии 3-2 с повышением температуры до Т₁ и, наконец, сжимается изотермически по линии 2-1, отдавая тепло горячему теплоприёмнику в количестве q₁=q₂+q₀ при температуре Т₁, чем и завершается цикл.

Машина, работающая по обратному циклу, называется холодильной машиной.

Из рассмотрения обратного цикла Карно можно сделать вывод, что передача теплоты от источника с низкой температурой к источнику с высокой температурой, как это следует из постулата Клаузиуса, обязательно требует затраты энергии (не может совершаться «даровым», процессом без компенсации).

Характеристикой эффективности холодильных машин является холодильный коэффициент:

(2.39)

Используя те же соотношения, что и при анализе прямого цикла Карно, получим выражение для определения холодильного коэффициента обратного цикла Карно:

. (2.40)

Холодильный коэффициент обратного цикла Карно зависит от абсолютных температур Т₂ и Т₁источников теплоты и обладает наибольшим значением по сравнению с холодильными коэффициентами других циклов, протекающих в тех же пределах температур.

ЦИКЛ РЕНКИНА

Основным циклом паросиловой установки является цикл Ренкина. Преобразование энергии органического или ядерного топлива в механическую при помощи водяного пара осуществляется в паросиловых установках (п.с.у.), которые являются базой современной теплоэнергетики (рис. 2.9).

Рис. 2.9. Принципиальная тепловая схема паросиловой установки

За начальное состояние здесь принята вода при некоторой температуре (точка 3, рис. 2.10), которая насосом сжимается (по 3 – 4) и подается в котелК при давленииP₁. Здесь происходит нагревание воды при постоянном давлении (процесс 4 – 5) до температуры кипения (точка 5), затем происходит парообразование (процесс 5 – 6). Полученный сухой насыщенный пар в пароперегревателе ПП перегревается до требуемой температуры t₁ (процесс 6-1).

Перегретый пар, имеющий параметры P₁ и t₁,по паропроводу поступает в паровую турбину Т, где происходит адиабатное расширение до давленияP₂с совершением технической работы (процесс 1 – 2). После турбины пар поступает в конденсатор Кон., который представляет собой трубчатый теплообменник. Внутренняя поверхность трубок охлаждается циркулирующей водой.

В конденсаторе при помощи охлаждающей воды от пара отнимается теплота парообразования (q₂) и пар переходит при постоянных давлении р₂ и температуре t₂ в жидкость (процесс конденсации 2 – 3). В дальнейшем цикл повторяется. Рассмотренный основной цикл паросиловой установки называется циклом Ренкина или простым конденсационным циклом.

Рис. 2.10. Основной цикл п. с. у. (цикл Ренкина) в р – v – (a)

и Т – s – координатах (б)

В цикле Ренкина осуществляется полная конденсация пара с последующим адиабатным сжатием 3 – 4 конденсата в насосе, что уменьшает полезную работу пара при его адиабатном расширении в трубке.

Термический к. п. д. цикла Ренкина может быть вычислен по общему выражению (2.36).

Теплота q₁ сообщается на участках 4–5–6–1 (рис. 2.10) при постоянном давлении ее можно найти какq₁ = i₁–i′₂, где i₁ –энтальпия пара, поступающего в турбину, измеряемая пл. 00'45612'; i₁ – энтальпия поступающей в котел жидкости (конденсата), измеряемая пл. 00'33'.

Рис. 2.11 График обратимого 1–2 адиабатного процесса расширения

на i – s –диаграмме

Теплота, отдаваемая паром в конденсаторе также при постоянном давлении, на участке 2 –3 будет равна:

q₂ = i₂ – i′₁,

где i₂ – энтальпия пара, выходящего из турбины, измеряемая пл. 00'322'. Тогда:

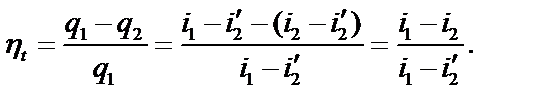(2.41)

Легко видеть, что подведенная в цикле теплота q1 будет измеряться пл. 45612'3'4, отведенная q₂ – пл. 22'3'32, а полезно использованная q₀= q₁–q₂ – пл. 456124.

Удобно определять к. п. д. цикла паросиловой установки при помощи i – s – диаграммы, где i₁– i₂ определяются по известным начальным и конечным параметрам адиабатного процесса расширения пара в турбине (рис. 2.11); i′₂ определяется по таблицам насыщенного пара для давления P₂.

Важной расчетной характеристикой цикла является удельный расход пара d₀, представляющий собой отношение часового расхода пара в идеальном двигателе D₀ к выработанной электроэнергии N. Так как 1 кг пара совершает в теоретическом цикле q₀ = i₁ – i₂ полезной работы, а 1 квт-час = 3600 кДж, то из уравнения теплового баланса идеального двигателя:

D₀ (i₁ – i₂) = 3600N;

получаем выражение для теоретического удельного расхода пара:

(2.42)

Анализ уравнения (2.42) показывает, что для увеличения термического к.п.д. цикла Ренкина необходимо увеличивать энтальпию пара перед турбиной i ₁ путём повышения Р₁ и t₁ и понижать давление пара в конденсаторе Р₂. Однако при работе даже на максимально возможных технически достижимых параметрах пара термический к.п.д теоретического цикла тепловой электростанции (ТЭС) с конденсационными турбинами не превышает 45-47%, а с учётом всех тепловых, механических и электрических потерь – не более 30-35%.

В этой связи в нашей стране получил широкое распространение метод комбинированной выработки электроэнергии и тепла (теплофикация) на базе теплоэлектроцентралей (ТЭЦ), оборудованных ПСУ с теплофикационными турбинами. Такие установки позволяют значительно повысить экономичность использования тепла (до 70-80% и выше) за счёт полезного использования значительной части раньше терявшегося тепла на q₂ промышленные и коммунально – бытовые нужды.

Дата добавления: 2017-01-14