Линзы и их основные характеристики. Формула тонкой линзы

Законы отражения и преломления. Полное внутреннее отражение.

При падении света на границу раздела двух сред часть света отражается в первую среду, а часть проходит во вторую среду, если она прозрачна, изменяя при этом направление своего распространения, т. е. преломляется.

Закон отражения. Угол падения равен углу отражения (a = b). Падающий луч AO, отраженный луч OB и перпендикуляр OC, восставленный в точке падения, лежат в одной плоскости (рис. 1).

Законы преломления. Луч падающий AO и преломленный OB лежат в одной плоскости с перпендикуляром CD, проведенным в точке падения луча к плоскости раздела двух сред (рис. 2). Отношение синусов угла падения а и угла преломления р постоянно для данных двух сред и называется показателем преломления второй среды по отношению к первой: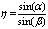

Угол падения, при котором свет не преломляется в другую среду, а отражается и скользит вдоль раздела двух сред (т.е. угол преломления равен 90⁰), называется предельным углом полного отражения.

Условие полного внутреннего отражения:

Линзой называется прозрачное тело, ограниченное с двух сторон криво- линейной поверхностью. (В частном случае одна из поверхностей̆ может быть плоской̆). По внешней форме линзы делятся на двояковыпуклые; плосковыпуклые; двояковогнутые; плосковогнутые; выпукло-вогнутые.
Линза называется тонкой̆, если ее толщина значительно меньше, чем радиусы кривизны 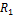и обеих поверхностей. На оптических схемах линзы обычно
обозначают двунаправленной̆ стрелкой.
Радиус кривизны R > 0 для выпуклой̆ поверхности; R < 0 для вогнутой̆.
Прямая проходящая через центры кривизны поверхностей линзы называется главной̆ оптической̆ осью.
Оптическим центром линзы (обычно обозначается O) называется точка, лежащая на главной̆ оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь.
Побочными оптическими осями
называются прямые, проходящие через оптический центр линзы и не совпадающие с главной оптической осью.
Фокусом линзы F называется точка, лежащая на главной оптической оси, в которой пересекаются лучи параксиального (приосевого) светового пучка, распространяющиеся параллельно главной оптической оси.
Фокальной плоскостью называется плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.

Фокусным расстоянием f называется расстояние между оптическим центром линзы O и ее фокусом F:

Величина Ф = называется оптической силой линзы. Линзы с положительной оптической силой являются собирающими а с отрицательной рассеивающими.

Формула тонкой линзы

Где а и в расстояние от линзы до предмета и его изображения. Если т.е лучи падают на линзу параллельным пучком (а) то b = f.

Если т.е. изображение находиться в бесконечности, и следовательно, лучи выходят из линзы параллельным пучком то а = f.

Дата добавления: 2017-01-14