Формули Байеса

Формула Байеса.

Сформулюємо задачу. Нехай подія А може з’явитися за умови появи однієї з несумісних подій В₁, В₂,..., В_n,які ми назвали гіпотезами і які складають повну групу. Ймовірність появи події А визначається за формулою повної ймовірності Р(А)=Р(В₁)·Р_В1(А) + Р(В₂)·Р_В2(А) + … + Р(В_n)·Р_Вn(А)

Припустимо, що відбулося випробування, в результаті якого з’явилась подія А. Спробуємо визначити, як змінились (в зв’язку з ти, що подія А вже відбулася) ймовірності гіпотез.

Іншими словами, будемо шукати умовні ймовірності Р_А(В₁), Р_А(В₂),..., Р_А(В_n)

Знайдемо спочатку ймовірність Р_А(В₁).

З теореми множення ймовірностей залежних подій маємо

Р(АВ₁)=Р(А)*Р_А(В₁)=Р(В₁)*Р_В1(А), значить

Р_А(В₁)= Р(В₁) *Р_А(В₁)/Р(А),

Де Р(А) обчислюємо за формулою повної ймовірності

Аналогічно виводяться формули для визначення умовних ймовірностей інших гіпотез. В загальному вигляді можна записати:

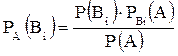
Наприклад:

§ Для участі в студентських відбірних спортивних змаганнях виділено з першої групи курсу -4, з другої – 6, із третьої групи – 5 студентів. Ймовірність того, що студент першої, другої і третьої груп потрапить в збірну, відповідно дорівнюють 0,9, 0,7 та 0,8. Навмання вибраний студент в результаті змагання потрапив у збірну. До якої з груп найімовірніше належав цей студент?

Схема розв’язку задач з використанням формули Бейеса:

Наприклад:

§ В першому ящику знаходиться 20 деталей, з них 15 стандартних; в другому ящику – 30 деталей, з них 24 стандартні; в третьому – 10 деталей,з них 6 стандартні. Обчислити ймовірність того, що навмання витягнута деталь із навмання взятого ящика – стандартна.

Питання для самоконтролю

1. Теорема додавання ймовірностей. Протилежні події

2. Залежні та незалежні події. Умовна ймовірність

3. Теорема множення ймовірностей

4. Ймовірність появи хоча б однієї події

5. Формула повної ймовірності

6. Формула Байеса

Тема 3. Схема незалежних випробувань

Лекція 3.

Послідовності незалежних випробувань

Мета: сформувати знання основних теорем на послідовності незалежних випробувань: Бернуллі, Муавра – Лапласа, Пуассона

План лекції:

1. Повторні незалежні випробування

2. Формула Бернуллі

3. Локальна теорема Муавра – Лапласа

4. Інтегральна теорема Муавра – Лапласа

5. Теорема Пуассона для малоймовірних подій

Рекомендована література: [1] ст. 55-63, [4] ст. 61-72, [6] ст. 67-82

1. Послідовності незалежних випробувань

Різноманітні події, такі наприклад, як:

- вироблена в деяких постійних технологічних умовах деталь виявиться стандартною,

- за час t відбудеться розкладання радіоактивної речовини,

- під час опускання жетону турнікет в метро спрацює вірно і дуже багато інших можна описати однією схемою.

Кожна така подія з’являється в кожному випробуванні з однією і тією ж ймовірністю, яка не змінюється, якщо становляться відомими результати попередніх випробувань. Такі випробування будемо називати незалежними. І будемо вважати, що ці випробування можуть бути повторені як завгодно велику кількість разів.

Розглянуту послідовність незалежних випробувань називають схемою Бернуллі.

2. Формула Бернуллі

Сформулюємо задачу. Необхідно обчислити ймовірність того, що подія, яка відповідає умовам схеми Бернуллі, в n незалежних випробуваннях з’явиться рівно k разів.

Теорема 3.1. (Формула Бернуллі) Якщо ймовірність р появи події А в кожному незалежному випробуванні постійна, то ймовірність Р_n(k) того, що подія А з’явиться рівно k раз в n незалежних випробуваннях обчислюється за формулою:

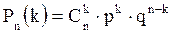
Приклад:

В цеху працює 6 моторів. Для кожного мотора ймовірність того, що він в даний момент включений, дорівнює 0,8. Обчислити ймовірність того, що в даний момент

§ 1. Включені 4 мотора

§ 2. Включені всі мотори

§ 3. Включені не менше п’яти моторів

3. Локальна теорема Муавра – Лапласа.

Якщо ймовірність появи події А в кожному незалежному випробуванні постійна, то ймовірність того, що в n незалежних випробуваннях вона відбудеться k разів, при будь-якій кількості випробувань n визначається за формулою Бернуллі. Але коли кількість випробувань велика, то обчислення шуканих ймовірностей за формулою Бернуллі становиться дуже громіздким.

Теорема 3. 2. (Локальна теорема Муавра - Лапласа) Якщо ймовірність р появи події А в кожному незалежному випробуванні постійна і відмінна від нуля, то ймовірність Р_n(k) того, що подія А з’явиться k раз в n незалежних випробуваннях наближено дорівнює значенню функції

,

де ,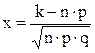

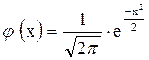
Функція 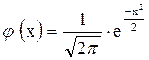- таблична і парна.

Приклад:

§ Знайти ймовірність того, що в 600 незалежних випробуваннях подія з’явиться рівно 250 раз, якщо ймовірність її появи в кожному випробуванні дорівнює 0,4.

4. Інтегральна теорема Муавра – Лапласа.

Сформулюємо задачу. Необхідно обчислити ймовірність того, що подія, яка відповідає умовам схеми Бернуллі, в n незалежних випробуваннях з’явиться не менше ніж k₁ раз і не більше ніж k₂ рази, за умови, що кількість випробувань n досить велика.

Теорема 3.3. (Інтегральна теорема Муавра – Лапласа). Якщо ймовірність р появи події А в кожному незалежному випробуванні постійна і відмінна від нуля та одиниці, то ймовірність Р_n(k₁, k₂) того, що подія А з’явиться в n незалежних випробуваннях від k₁ до k₂ раз наближено дорівнює визначеному інтегралу

де ,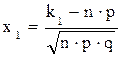

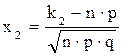
Функція 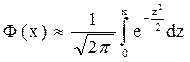називається функцією Лапласа. Її значення занесені в таблицю. Функція Лапласа – непарна.

Для того, щоб мати змогу скористатися функцією Лапласа перетворимо її:

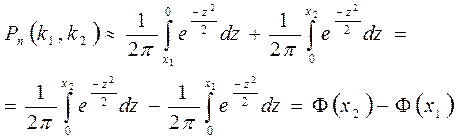
Отже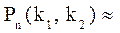

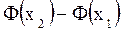
Приклад:

Ймовірність влучення стрілком в мішень при одному пострілі дорівнює 0,75. Обчислити ймовірність того, що при 100 пострілах в мішень буде влучено:

§ 1. Не менше 70 і не більше 80 разів

§ 2. Не більше 70 разів

5. Теорема Пуассона для малоймовірних подій

Нехай проводиться n незалежних випробувань, в кожному з яких подія А може або з’явитися, або не з’явитися з однаковою ймовірністю р. Розглянемо в якості ДВВ Х – кількість появ події А в таких випробуваннях.

Якщо ймовірність появи події А у всіх випробуваннях дуже мала (p≤0,1), то ймовірності, що відповідають можливим значенням ДВВ Х обчислюється за формулою Пуассона

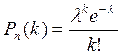, где =n·p

Питання для самоконтролю

1. Повторні незалежні випробування

2. Формула Бернуллі

3. Локальна теорема Муавра – Лапласа

4. Інтегральна теорема Муавра – Лапласа

5. Теорема Пуассона для малоймовірних подій

Тема 4. Випадкові величини та їх економічна інтерпретація

Лекція 4.

Випадкові величини

Мета: ввести означення одновимірних випадкових величин, методів їх представлення.

План лекції:

1. Означення одновимірної випадкової величини, її закон розподілу

2. Функція розподілу ймовірності випадкової величини та її властивості

3. Щільність розподілу

4. Економічна інтерпретація випадкових величин

Рекомендована література: [1] ст. 55-63, [4] ст. 61-72, [6] ст. 67-82

1. Означення одновимірної випадкової величини, її закон розподілу

Випадковою називають величину, яка в результаті випробування приймає те чи інше (але при цьому тільки одне) можливе значення, наперед невідоме, таке, що змінюється від випробування до випробування і залежить від випадкових обставин.

На відміну від випадкової події, яка є якісною характеристикою випадкового результату випробування, випадкова величина характеризує результат випробування кількісно.

Дискретною називають випадкову величину, що приймає окремі, ізольовані можливі значення з визначеними ймовірностями.

Цілочисловою називають ДВВ, можливі значення якої приймають тільки цілі значення з будь – якого обмеженого або необмеженого проміжку.

Неперервною називають випадкову величину, що може приймати будь-які значення з деякого обмеженого або необмеженого проміжку.

Випадкові величини прийнять позначати останніми великими літерами латинського алфавіту Х, Y, Z, а їх можливі значення – відповідними малими літерами.

Законом розподілу дискретної випадкової величини (ДВВ) називають будь – яке співвідношення, що встановлює зв’язок між можливими значеннями випадкової величини та відповідними їм ймовірностями.

Для ДВВ закон розподілу може бути задано:

- у вигляді таблиці

Х
р

- аналітично (тобто за допомогою формули)

- графічно (цей вид завдання закону розподілу використовують для наочності. На графіку відкладають можливі значення ВВ та відповідні їм ймовірності. Точки сполучає ламана, яку називають багатокутником або полігоном розподілу).

Приклад:

Два стрілки здійснюють по одному пострілу в мішень. Ймовірність влучення в неї першим стрілком дорівнює 0,5, другим – 0,4. Скласти закон розподілу кількості влучень в мішень і побудувати полігон розподілу

Математичні дії над випадковими величинами:

Нехай задано дві випадкові величини

Х	х1	х2		хn
р	р1	р2		рn

Y	y1	y2		yn
р	р1	р2		рn

Добутком kX випадкової величини Х на постійну величину k називається випадкова величина, що приймає значення kx_i з тими самими ймовірностями p_i.

Приклад:

ДВВ задано законом розподілу. Побудувати закон розподілу ДВВ Y=3X

Х	-2
р	0.1	0.3	0.2	0.3	0.1

При піднесенні випадкової величини Х до степеня m отримаємо випадкову величину з тими самими ймовірностями p_i.

Приклад:

§ ДВВ задано законом розподілу. Побудувати закон розподілу ДВВ Y=X²

Х	-2
р	0.1	0.3	0.2	0.3	0.1

Алгебраїчною сумою випадкових величин Х і У називається випадкова величина, що приймає можливі значення виду 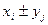і ймовірності 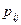того, що випадкова величина Х прийме значення 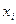, а випадкова величина У – значення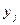

Приклад:

ДВВ задано законом розподілу. Побудувати закон розподілу ДВВ

Z=X+Y

Х	-2
р	0.1	0.3	0.2	0.3	0.1

Y	-3	-2
р	0.2	0.1	0.15	0.35	0.2

Добутком випадкових величин Х і У називається випадкова величина, що приймає можливі значення виду 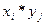і ймовірності 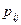того, що випадкова величина Х прийме значення 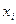, а випадкова величина У – значення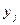

Приклад:

ДВВ задано законом розподілу. Побудувати закон розподілу ДВВ

Z=X*Y

Х	-2
р	0.1	0.3	0.2	0.3	0.1

Y	-3	-2
р	0.2	0.1	0.15	0.35	0.2

2. Функція розподілу ймовірностей випадкової величини та її властивості.

Функцією розподілу ВВ Х називається функція F(x), яка визначає для кожного х ймовірність того, що ВВ Х прийме значення менше ніж х, тобто

Наприклад: ВВ задано законом розподілу:

Х
р	0,4	0,1	0,3	0,2

Побудувати її функцію розподілу.

Властивості функції розподілу ВВ:

1. Функція розподілу ВВ – невід’ємна функція, що належить проміжку від нуля до одиниці

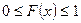
2. Функція розподілу ВВ – неспадна функція на всій числовій осі

Наслідок: Ймовірність того, що випадкова величина прийме значення, що належать проміжку , дорівнює приросту функції розподілу на цьому проміжку, тобто

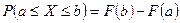
3. Якщо можливі значення належать інтервалу (a, b), то F(x)=0, якщо 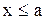і F(x)=1, якщо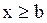

Дата добавления: 2017-02-01