Тема 10. Первинне опрацювання статистичних даних

Тема 11. Статистичне та інтервальне оцінювання параметрів розподілу

Лекція 8.

Основні поняття математичної статистики

Мета: сформувати знання основних понять математичної статистики, вести поняття про вибірковий метод аналізу статистичної інформації, можливості її графічного представлення.

План лекції:

1. Генеральна та вибіркова сукупності. Поняття про теоретичний та емпіричний розподіли. Варіаційний ряд

2. Статистичний розподіл вибірки. Полігон та гістограма

3. Емпірична функція розподілу та її властивості

4.Числові характеристики вибірки

Рекомендована література: [1] ст. 64-94, [4] ст. 83-103, [6] ст. 86-166

1. Генеральна та вибіркова сукупності. Поняття про теоретичний та емпіричний розподіли. Варіаційний ряд.

Мета кожного дослідження – виявлення закономірностей явищ, які спостерігають, та використання цих закономірностей у повсякденній практичній діяльності. Для встановлення цих закономірностей проводять спеціальні досліди та спостерігають одиничні явища. Далі роблять узагальнений висновок у вигляді закону.

У тих випадках, коли явище знаходиться під дією багатьох факторів, застосовують інший метод вивчення – статистичний, тобто систематизація та обробка статистичних даних однорідних дослідів.

Досить часто статистичний метод використовують в економіці, соціології, політології.

Предмет математичної статистики полягає в розробці методів збору та обробки статистичних даних для одержання наукових та практичних висновків.

Основні задачі математичної статистики:

1. вказати способи збору та групування статистичних відомостей

2. визначити закон розподілу ВВ або системи ВВ за статистичними даними

3. визначити невідомі параметри розподілу

4. перевірити правдоподібність припущень про закон розподілу ВВ, про форму зв’язку між ВВ-нами або про значення параметру, який оцінюють

Нехай потрібно вивчити сукупність об’єктів відносно деякої якісної або кількісної ознаки, які характеризують ці об’єкти.

Кожен об’єкт, який спостерігають, має декілька ознак. Розглядаючи лише одну ознаку кожного об’єкта, припускають, що інші ознаки рівноправні. Таку множину об’єктів називають – однорідною.

Множини однорідних об’єктів називають статистичними сукупностями.

Кількісні ознаки статистичної сукупності можуть бути:

- дискретними

- неперервними

Вся сукупність об’єктів, що підлягає вивченню, називається генеральною сукупністю

Генеральна сукупність є теоретичним розподілом властивостей об’єктів, що вивчаються.

Однак, кількість об’єктів, що входять до генеральної сукупності може бути досить великою, тому не завжди доцільно досліджувати всю сукупність, а випадково вибрати з неї деяку меншу кількість об’єктів.

Кількість об’єктів, що відібрано безпосередньо для вивчення із генеральної сукупності, називається вибірковою сукупністю, або просто вибіркою.

Вибірка представляє собою емпіричний (отриманий дослідним шляхом) розподіл властивостей об’єктів, що вивчають.

Сутність вибіркового методу полягає в тому, щоб по деякій частині генеральної (по вибірці) можна було зробити висновок про її властивості в цілому.

Основні переваги вибіркового методу:

1. дає змогу суттєво зекономити витрати ресурсів (матеріальних, трудових, часових)

2. є єдино можливою у випадку нескінченої генеральної сукупності, або у випадку, коли дослідження пов’язане із знищенням об’єктів, що спостерігають (строк гідності, максимальний час роботи приладу)

Однак, для того, щоб по даним вибірки можна було зробити висновок про властивості всієї генеральної сукупності – ця вибірка повинна бути репрезентативною (вибірка повинна проводитись випадково і всі об’єкти вибірки повинні мати однакову ймовірність потрапити у вибірку)

Вибірки можуть бути двох типів:

- повторна – вибірка, в якій відібраний об’єкт перед відбором наступного об’єкту повертається в генеральну сукупність

- безповторна – вибірка, в якій відібраний об’єкт перед відбором наступного об’єкту не повертається в генеральну сукупність

Об’ємом сукупності (генеральної або вибіркової) називають кількість об’єктів цієї сукупності.

Об’єм генеральної сукупності будемо позначати N

Об’єм вибіркової сукупності будемо позначати n

Нехай із генеральної сукупності взята вибірка об’єктів для вивчення деякої ознаки Х, яка прийняла значення х₁ – n₁ раз, значення х₂ – n₂ раз,..., значення х_m – n_m раз.

Значення х₁, х₂,..., х_m називають варіантами ознаки Х, значення n₁, n₂,..., n_m - називають частотами, а їх суму n₁+ n₂+...+ n_m =n– об’ємом вибірки.

Відношення частот до об’єму вибірки називають відноснимичастотами(частістю)

Варіанти, що записані у зростаючому порядку називають варіаційним рядом

2. Статистичний розподіл вибірки, полігон і гістограма

Статистичним розподілом вибірки називають перелік варіант, записаний у зростаючому порядку та відповідних їм частот (або відносних частот)

Для наочності будують різноманітні графіки статистичного розподілу, такі як полігон та гістограму.

Полігоном частот (відносних частот) наз ломану, відрізки якої сполучають точки (х_і, n_і)((x_i, W_i))

Гістограмою частот (відносних частот) називають ступінчасту фігуру, що складається з прямокутників, основою яким слугують часткові інтервали довжиною h, а висота дорівнює відношення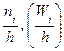

3. Емпірична функція розподілу та її властивості

Емпіричною функцією розподілу (функцією розподілу вибірки) називають функцію F*(x), яка визначає для кожного значення х частість події Х<х

де n_х – кількість варіант, які менше від х

n – об’єм вибірки

4. Числові характеристики вибірки

Ø Простою середньоарифметичною вибірки називають суму варіант вибірки, поділену на об’єм вибірки

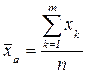
Ø Вибірковою середньою або зваженою середньоарифметичною називають середню арифметичну варіант вибірки з врахуванням їх частостей

де x_k – варіанти вибірки

– об’єм вибірки

Ø Вибірковою дисперсією називають середню квадратів відхилення варіант від вибіркової середньої з урахуванням відповідних частостей

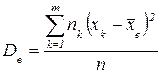
Обчислення вибіркової дисперсії спрощується, якщо її знаходити за формулою

або - вибіркова дисперсія дорівнює вибірковій середній квадратів значень мінус квадрат вибіркової середньої

Ø Вибірковим середньоквадратичним відхиленням називають квадратний корінь із вибіркової дисперсії

5. Точкові статистичні оцінки та їх властивості.

У багатьох випадках потрібно дослідити саме кількісну ознаку Х генеральної сукупності. Враховуючи те, що генеральна сукупність може бути досить великою, то зробити це було б зручніше за результатами вибірки. Часто для цього досить знати наближені значення математичного сподівання, дисперсії, СКВ та ін.

Досить часто за результатами вибірки вдається встановити закон розподілу Х (біноміальний, Пуассона, нормальний і т. д.). В цьому випадку потрібно вміти оцінити параметри цього розподілу.

Статистичною оцінкою невідомого параметра випадкової величини Х генеральної сукупності (теоретичного розподілу Х) називають функцію від випадкових величин (результатів вибірки), що спостерігаються.

Щоб статистичні оцінки давали найбільші наближення параметрів, вони повинні відповідати наступним вимогам:

1. Статистична оцінка повинна бути незсунутою

Незсунутою називають статистичну оцінку θ^* деякого параметра θ, якщо її математичне сподівання дорівнює самому параметру для б-я об’єму вибірки

М(θ*)=θ

Ця вимога захищає оцінюваний параметр від систематичних (невипадкових з одним знаком) помилок

2. Статистична оцінка повинна бути ефективною

Ефективною називають таку статистичну оцінку θ*, яка при заданому об’єму вибірки п має найменшу можливу дисперсію

Якомога менше значення дисперсії виключає великі помилки (промахи)

3. Статистична оцінка повинна бути обґрунтованою

Обґрунтованою називають статистичну оцінку θ*, яка при п→∞ прямує за ймовірністю до оцінюваного параметру

Тобто справджується закон великих чисел (чим більший об’єм вибірки тим точніша оцінка)

Оцінка параметру розподілу генеральної сукупності, що визначається одним числом, називаютьивається точковою

6. Генеральні середня, дисперсія та середнє квадратичне відхилення.

Генеральною середньою х_г^-називають середнє арифметичне значень ознаки генеральної сукупності:

Обчислювати генеральну середню не зручно, а інколи навіть неможливо. В цьому випадку її оцінюють за даними вибірки.

Можна довести, що незсунутою оцінкою генеральної середньої є вибіркова середня, тобто

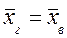
Якщо початкові варіанти x_i великі, то для спрощення підрахунку доцільно відняти від кожної варіанти одне й те ж число С, тобто перейти до умовних варіант u_i=x_i – C. В якості числа С зручно прийняти число, наближене до середньої вибіркової. В цьому випадку

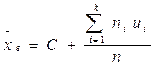
v Генеральною дисперсією називають середнє арифметичне квадратів відхилень значень ознаки генеральної сукупності від їх середнього значення х_г^-

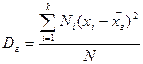
Вибіркова дисперсія є зсунутою оцінкою генеральної дисперсії

Якщо початкові варіанти x_i великі, то для спрощення обчислення доцільно відняти від кожної варіанти одне й те ж число С, тобто перейти до умовних варіант u_i=x_i – C. В якості числа С зручно використати число, близьке до вибіркової середньої. Дисперсія при цьому не зміниться, тобто

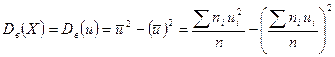
Однак, оцінювати генеральну дисперсію по можливим значенням вибірки не можна, так як вибіркова дисперсія дає зміщену статистичну оцінку. Щоб виправити цей недолік використовують виправлену дисперсію, що обчислюється за формулою:

v Генеральним середньоквадратичним відхиленням (стандартом) називають квадратний корінь з генеральної дисперсії

Для оцінки середнього квадратичного відхилення генеральної сукупності використовують виправлене СКВ, що дорівнює квадратному кореню з виправленої дисперсії

Виправлене СКВ не є незсунутою оцінкою генеральної сукупності

Якщо початкові варіанти x_i - десяткові дроби з k десятковими знаками після коми, то, щоб уникнути дій з дробами, помножають початкові варіанти на постійне число С=10 ^k. При цьому дисперсія збільшується в С² раз. Отже, після того, як обчислена дисперсія в умовних варіантах, її потрібно розділити на С²:

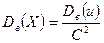
а вибіркову середню поділити на С:

7. Інтервальні оцінки

Інтервальною називають оцінку, яка визначається двома числами – кінцями інтервалу.

Надійністю (довірчою ймовірністю) оцінки параметра θ за θ* називають ймовірність

з якою виконується нерівність

де - точність оцінки

t – аргумент функції Лапласа

σ – СКВ

n – об’єм вибірки

Інтервал 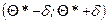називають довірчим, якщо він покриває невідомий параметр θ із заданою надійністю γ

Довірчий інтервал для оцінки математичного сподівання нормального розподілу обчислюють за формулою:

Можна показати, що

Питання для самопідготовки

1. Генеральна та вибіркова сукупності. Поняття про теоретичний та емпіричний розподіли. Варіаційний ряд.

2. Статистичний розподіл вибірки. Полігон та гістограма.

3. Емпірична функція розподілу та її властивості.

5. Числові характеристики вибірки.

6. Точкові статистичні оцінки та їх властивості.

7. Генеральні середня, дисперсія та середнє квадратичне відхилення.

8. Інтервальні оцінки.

9. Довірчі інтервали для математичного сподівання нормального розподілу.

Тема 12. Перевірка статистичних гіпотез

Тема 13. Елементи теорії регресії

Тема 14. Елементи теорії кореляції

Лекція 9.

Статистична перевірка статистичних гіпотез. Елементи теорії регресії та кореляції

Мета: сформувати знання з основ статистичної перевірки статистичних гіпотез, розглянути деякі критерії перевірки нульової гіпотези; сформувати знання з основ теорії регресійного та кореляційного аналізу.

План лекції:

1. Поняття статистичної гіпотези. Нульова і конкуруюча гіпотези, помилки першого та другого родів. Статистичний критерій перевірки нульової гіпотези

2. Функціональна, статистична та кореляційна залежності

3. Вибірковий коефіцієнт та вибіркове рівняння регресії

4. Лінійна та нелінійна регресія

Рекомендована література: [1] ст. 281-287, 288-293, 329-333, [4] ст. 197-205, [6] ст. 368-371

1. Поняття статистичної гіпотези. Нульова і конкуруюча гіпотези, помилки першого та другого родів.

Одними з основних задач математичної статистики є задачі визначення закону розподілу випадкової величини або визначення невідомих параметрів відомого закону розподілу.

Оскільки закон розподілу або параметри закону розподілу невідомі, то можна висунути певні припущення щодо виду закону або величини параметрів.

Статистичною називають гіпотезу щодо виду невідомого закону розподілу, або про невідомі параметри відомого закону розподілу.

Оскільки можна висунути гіпотезу про закон розподілу або про параметри розподілу, то можна висунути і гіпотезу, що буде суперечити висунутій.

Якщо висунута гіпотеза буде відкинутою, то суперечна їй гіпотеза отримує право на існування.

Такі гіпотези отримали назви:

Нульова (основна) гіпотеза – гіпотеза, що висунули і будуть перевіряти на можливість її існування. Позначається Н₀

Конкуруюча (альтернативна) гіпотеза – гіпотеза, що суперечить висунутій основній гіпотезі. Позначають Н₁.

Нульова гіпотеза може бути 2 видів:

1. Проста гіпотеза містить тільки одне припущення щодо закону розподілу або параметрів розподілу

1. Складна гіпотеза містить декілька припущень

Оскільки висунута гіпотеза може бути правильною або не правильною, виникає необхідність її перевірити.

Перевіряють статистичні гіпотези статистичними методами (тобто використовуючи неодноразові випробування).

В результаті перевірки висунута гіпотеза може бути або прийнятою або відкинутою. У зв’язку з прийняттям рішення про прийняття або відкинення висунутої гіпотези можуть виникнути помилки 2 родів:

Помилка першого роду полягає в тому, що буде відкинуто правильну гіпотезу

Помилка другого роду полягає в тому, що буде прийнято невірну гіпотезу

Для того, щоб за результатами випробувань прийняти або відкинути нульову гіпотезу, її потрібно порівняти з яким-небудь еталоном, що відповідав би обраному в якості гіпотези закону розподілу або параметру розподілу.

В якості такого еталону виступає певна величина, що називають статистичним критерієм.

Статистичним критерієм називають випадкову величину К, що використовується для перевірки нульової гіпотези

Статистичний критерій – величина отримана теоретично.

Спостереженим значенням К_сп називають значення критерію, що обчислений за даними вибірок (емпірично)

Після того, як обраний статистичний критерій для перевірки нульової гіпотези, множина всіх його можливих значень розбивається на дві підмножини:

Одна з них містить значення критерію, при яких нульова гіпотеза приймається, інша – значення критерію, при яких нульова гіпотеза відкидається

Критичною областю називають сукупність значень критерію, при яких нульову гіпотезу відкидають

Областю прийняття гіпотези називають сукупність значень критерію, при яких нульову гіпотезу приймають.

Критичну область від області прийняття гіпотези відділяють точки, що отримали назву критичних k_кр

Існують 3 види критичних областей:

1. Правостороння критична область задається нерівністю К>k_кр, де k_кр>0

2. Лівостороння критична область задається нерівністю К<k_кр, де k_кр<0

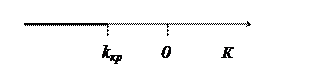
3. Двостороння критична область задається нерівностями К<k₁, К>k₂, де k₂> k₁

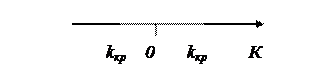
Головний принцип перевірки статистичних гіпотез:

Якщо спостережене значення належить критичній області, то нульову гіпотезу відкидають, якщо спостережене значення критерію належить області прийняття гіпотез – гіпотеза вважається вірною.

Якщо потрібно перевірити гіпотезу про невідомий закон розподілу, то висувається нульова гіпотеза, яка стверджує, що задана випадкова величина розподілена за певним законом розподілу.

Цю нульову гіпотезу потрібно перевірити.

Гіпотези, про невідомий вид закону розподілу перевіряють за допомогою критерію узгодження.

Таких критеріїв існує декілька, але найбільш часто застосовують критерій узгодження Пірсона (χ²)

Емпіричні частоти це частоти, що були фактично спостережені під час випробування

Теоретичні частоти це частоти, що обчислені за припущення, що відомий закон розподілу генеральної сукупності

Приклад Обчислити теоретичні частоти по заданому розподілу вибірки (припустивши, що ВВ розподілена за нормальним законом) та перевірити гіпотезу про нормальний закон розподілу заданої сукупності за критерієм Пірсона, якщо рівень значущості α=0,01

Вибірка: 4, 5, 8, 4, 7, 9, 11, 15, 4, 8, 9, 3, 15, 12, 11, 14, 17, 5, 8, 10, 5, 9, 11, 15, 20, 19, 17, 5, 16, 13, 7, 6, 20, 15, 4, 16, 3, 21, 18, 16, 5, 4, 6, 16, 18, 3, 6, 8, 19, 5, 12, 14, 16, 15, 18, 7, 3, 15, 14, 18, 20, 14, 16, 7, 6, 3, 16, 16, 15, 7, 20, 6, 4, 13, 14, 12, 18, 19, 9, 5, 7, 3, 20, 21, 14, 13, 8, 6, 4, 3, 7, 6, 16, 15, 16,14, 7, 9,4, 10

1. Обчислимо теоретичні частоти

Алгоритм обчислення теоретичних частот:

Для обчислення складемо розрахункову таблицю:

Границі інтервалу	Частота   ni	Границі інтервалу	Значення функції Лапласа	Ймовір-ність рі	Теоретич-ні частоти ni^т
хі	хі+1	zі	zі+1	Ф(zі)	Ф(zі+1)

2. Перевіримо гіпотезу про нормальний розподіл вибірки

Алгоритм перевірки нульової гіпотези про нормальний розподіл за критерієм Пірсона:

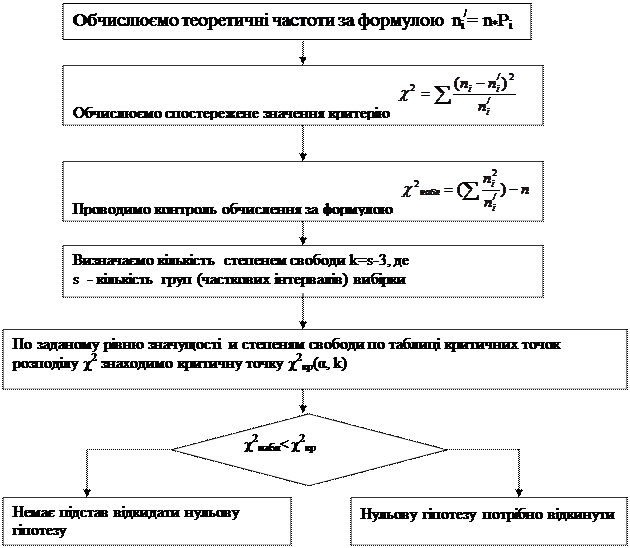ТАК НІ

За даними попередніх обчислень складемо розрахункову таблицю:

i	ni	ni^/	ni- ni^/	(ni- ni^/)^2		ni^2	ni^2/ ni^/
Σ

2. Функціональна, статистична та кореляційна залежності.

Під час вивчення явищ, що відбуваються в природі та суспільстві, необхідно їх розглядати в постійній залежності від іншого явища, або явищ.

Функціональною називають залежність в якій кожному значенню однієї змінної відповідає досить визначене значення іншої

Функціональна залежність між декількома величинами можлива лише у випадку, якщо на ці величини не впливають випадкові фактори. Отже в природі такі залежності зустрічаються досить рідко і використовуються частіше за все в точних науках (математиці, фізиці).

В економіці, соціології та інших прикладних науках функціональні залежності зустрічаються дуже рідко, так як кожному значенню однієї змінної може відповідати множина значень іншої змінної.

Статистичною називають залежність в якій кожному значенню однієї змінної відповідає множина можливих значень іншої.

Така залежність виникає тому, що на залежну змінну в ній впливає безліч випадкових факторів, які не завжди можна врахувати, а також тому, що вимірювання значень змінних завжди проводиться з випадковою похибкою.

Оскільки статистична залежність дуже неоднозначна (може приймати досить різні значення в однакових умовах), користуватися нею для дослідження різноманітних економічних, природних, соціальних та ін. явищ незручно. Тому, для дослідження таких залежностей, частіше використовують усереднену схему залежності.

Кореляційною залежністю між двома змінними величинами називають функціональна залежність між значеннями однієї з них та умовним математичним сподіванням іншої.

3. Вибірковий коефіцієнт та вибіркове рівняння регресії

В якості оцінок умовного математичного сподівання приймають умовні середні, що обчислюють за даними спостережень (по вибірці)

Умовним середнім називають середнє арифметичне значень У, що спостерігалися, відповідних Х=х

Умовним середнім 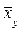називають середнє арифметичне значень Х, що спостерігалися, відповідних У=у

Рівняння виду називають вибірковим рівнянням регресії У на Х,

Функцію називають вибірковою регресією У на Х

Графік функції - вибірковою лінією регресії У на Х

Рівняння виду називають вибірковим рівнянням регресії Х на У,

Функцію називають вибірковою регресією Х на У

Графік функції - вибірковою лінією регресії Х на У

Пряма лінія регресії

Вибіркове рівняння прямої лінії регресії задається у вигляді:

-

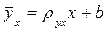для регресії У на Х

-

для регресії Х на У

Будемо розглядати систему кількісних ознак (Х, У). В результаті n незалежних випробувань отримано вибірку з n пар чисел ()

1. Якщо вибірка невеликого об’єму і пари чисел () з однаковими значеннями зустрічаються не часто

В цьому випадку проводиться обчислення параметрів вибіркового рівняння прямої лінії регресії по незгрупованим даним.

Параметри вибіркового рівняння регресії У на Х обчислимо за формулами:

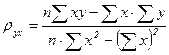
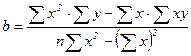
2. Якщо вибірка великого об’єму(більше 50) і пари чисел () з однаковими значеннями зустрічаються досить часто

В цьому випадку проводиться обчислення параметрів вибіркового рівняння прямої лінії регресії по групованим даним.

Для цього доцільно побудувати кореляційну таблицю.

Наприклад: По даним вибірки побудувати кореляційну таблицю, побудувати емпіричну лінію регресії У на Х, знайти та побудувати рівняння регресії У на Х

х	-1		-1	-1	-1	-1			-1
у	-2	-2			-2	-1	-2		-2	-2	-2

х							-1
у		-2		-2		-2	-1		-2	-2	-1		-2

1. Побудуємо кореляційну таблицю

У	Х	Σxi	середня групова
Σуj
середня групова

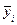
2. Обчислимо середні групові за формулами

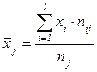
та занесемо їх до кореляційної таблиці

3. Побудуємо ламану, що сполучає точки . Така ламана називається емпіричною лінією регресії У на Х

4. Знайдемо вибіркове рівняння регресії за формулою

Для цього використаємо формули:

За рівнянням регресії на графіку зобразимо пряму лінію регресії У на Х

Коефіцієнт регресії У на Х вказує, на скільки одиниць в середньому змінюється величина У при збільшенні величини Х на одну одиницю.

Для того, щоб оцінити, наскільки щільно залежні величини, використовують вибірковий коефіцієнт кореляції:

Питання для самоконтролю

1. Поняття статистичної гіпотези. Нульова і конкуруюча гіпотези помилки першого та другого родів.

2. Статистичний критерій перевірки нульової гіпотези.

3. Критерій узгодження Пірсона.

4. Функціональна, статистична та кореляційна залежності

5. Вибірковий коефіцієнт та вибіркове рівняння регресії

6. Лінійна та нелінійна регресія

Дата добавления: 2017-02-01