Означення випадкового процесу.

Наприклад

Закон розподілу ДВВ задано у вигляді таблиці

Х
р	1/16	1/4	1/2	3/16

Побудувати функцію розподілу даної ДВВ та обчислити ймовірність Р(1,3<X<2,5)

3. Щільність розподілу.

Щільністю розподілу (диференційною функцією розподілу) f(x) НВВ

називається перша похідна від її функції розподілу, тобто

Властивості щільності розподілу:

1. Щільність розподілу – невід’ємна функція
2. Ймовірність попадання випадкової величини в проміжок дорівнює визначеному інтегралу в границях від а до b від її щільності розподілу, тобто

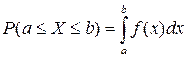
3. Функція розподілу може бути виражена через щільність розподілу за формулою:

4. Невласний інтеграл в нескінчених границях від щільності розподілу НВВ дорівнює одиниці, тобто

Наприклад:

НВВ задана своєю щільністю розподілу. Знайти функцію розподілу.

Наприклад: НВВ задана своєю функцією розподілу.

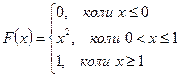Знайти щільність розподілу. Обчислити ймовірність того, що в результаті чотирьох незалежних випробувань ВВ рівно три рази прийме значення, що належить інтервалу (0,25; 0,75). Побудувати графіки F(x) та f(x).

Щільність розподілу НВВ називають також законом розподілу НВВ.

4. Економічна інтерпретація випадкових величин

За допомогою випадкових величин можна представляти велику кількість економічних процесів. Так, наприклад, суми вкладів, суми кредитування, кількість повернутих банку кредитів за певний проміжок часу, суми виплат за договорами страхування, розподіл пакетів акцій по власникам, показники роботи підприємства, банка, страхової компанії тощо – випадкові величини, які можна задати певними законами розподілу.

Питання для самоконтролю

1. Означення одновимірної дискретної випадкової величини

2. Закон розподілу ймовірностей одновимірної дискретної випадкової величини. Багатокутник розподілу

3.Означення одновимірної неперервної випадкової величини

4. Економічна інтерпретація випадкових величин

5. Функція розподілу ймовірностей випадкової величини та її властивості

6. Щільність розподілу

Тема 5. Закони розподілу та числові характеристики випадкових величин

Лекція 5.

Числові характеристики і закони розподілу випадкових величин

Мета: сформувати знання з використання числових характеристик одновимірних випадкових величин, розглянути рівномірний, показниковий та нормальний закони розподілу, функцію Лапласа.

План лекції:

1. Математичне сподівання, дисперсія, середнє квадратичне відхилення, їх властивості

2. Моменти. Мода та медіана

3. Рівномірний, показниковий та нормальний закони розподілу. Функція Лапласа

4. Біноміальний, геометричний гіпергеометричний, закон розподілу Пуассона

Рекомендована література: [1] ст. 55-63, [4] ст. 61-72, [6] ст. 67-82

1. Математичне сподівання, дисперсія, середнє квадратичне відхилення, їх властивості

Досить часто виникають ситуації, коли законом розподілу не дуже зручно користуватись
Інколи для аналізу випадкової величини зручніше використовувати числа, що описують цю величину сумарно. Такі числа називають числовими характеристиками випадкової величини. Найбільш часто використовують наступні числові характеристики:

1. Математичне сподівання

2. Дисперсію

3. Середнє квадратичне відхилення.

Математичним сподіванням ДВВ М(Х) називають суму добутків всіх її можливих значень на відповідні їм ймовірності, тобто

Приклад:

ВВ задано законом розподілом

Обчислити математичне сподівання заданої ДВВ

х	-1
р	0,1	0,3	0,25	0,35

Основні властивості математичного сподівання:

§ Математичне сподівання постійної величини дорівнює самій постійній, тобто М(С)=С

§ Постійний множник можна виносити за знак математичного сподівання, тобто М(С*Х)=С*М(Х)

§ Математичне сподівання добутку декількох взаємонезалежних ДВВ дорівнює добутку їх математичних сподівань, тобто

М(Х₁* Х₂*...*Х_n)= М(Х₁)* М(Х₂)*…* М(Х_n)

§ Математичне сподівання алгебраїчної суми ДВВ дорівнює алгебраїчній сумі їх математичних сподівань, тобто

М(Х₁± Х₂±...±Х_n)= М(Х₁)± М(Х₂)±…±М(Х_n)

Приклад:

Задано М(Х)=2,5 та М(У)=1,2. Обчислити М(2Х+3У)

Дисперсією ДВВ D(X) називають число, що дорівнює математичному сподіванню квадрата відхилення ДВВ від її математичного сподівання, тобто

D(X)=M((X-M(X))²)

Основні властивості дисперсії:

§ Дисперсія будь-якої ДВВ – невід’ємна

§ Дисперсія постійної величини дорівнює нулю

§ Постійний множник можна виносити за знак дисперсії, при цьому його потрібно піднести до квадрату, тобто D(C*X)=C²*D(X)

§ Дисперсію ДВВ можна також обчислювати за формулою:

D(X)=M(X²)-M²(X)

§ Дисперсія алгебраїчної суми ДВВ дорівнює сумі їх дисперсій, тобто D(X±Y)=D(X)+D(Y)

Приклад:

1. ВВ задано законом розподілом. Обчислити дисперсію заданої ДВВ

х	-1
р	0,1	0,3	0,25	0,35

2. Задано D(Х)=2,5 та D(У)=1,2. Обчислити D(2Х-3У)

Середньоквадратичним відхиленням ДВВ (Х) називають величину, що дорівнює квадратному кореню з дисперсії, тобто

(Х)=

Числові характеристики НВВ:

Як і у випадку з ДВВ, найбільш часто для характеристики НВВ використовують наступні числові характеристики: математичне сподівання, дисперсію та середньоквадратичне відхилення.

Математичним сподіванням НВВ Х, можливі значення якої належать проміжку , називають визначений інтеграл

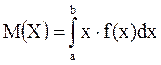
Дисперсією НВВ, можливі значення якої належать проміжку , називають визначений інтеграл

D(X)=

Для обчислення дисперсії використовують також наступну формулу:

D(X)=

Приклад. Обчислити математичне сподівання та дисперсію НВВ заданої функцією розподілу

§ F(x)=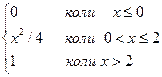

2. Моменти. Мода та медіана.

Початковим моментом порядку k випадкової величини Х називають математичне сподівання величини X^k .

Для дискретних випадкових величин:

Для неперервних випадкових величин:

Центральним моментом порядку k випадкової величини Х називають математичне сподівання величини , тобто

Для дискретних випадкових величин: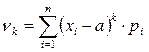

Для неперервних випадкових величин: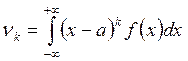

Розглянемо взаємозв’язок між початковими та центральними моментами:

- дисперсія

- характеризує асиметрію розподілу

- характеризує крутість (гостроверхість чи плосковерхість) розподілу.

Приклад. Обчислити центральний момент 3-го порядку для ДВВ заданої законом розподілу:

х	-1
р	0,1	0,5	0,4

Модою 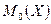випадкової величини Х називається її найбільш ймовірне значення.

Якщо ймовірність або щільність ймовірності досягають максимуму не в одній, а в декількох точках, розподіл випадкової величини називається полі модальним.

Медіаною випадкової величини Х називається таке її значення при якому

3. Рівномірний, показниковий та нормальний закони розподілу. Функція Лапласа.

Рівномірний закон розподілу.

Рівномірним називають розподіл ймовірностей НВВ Х, якщо на проміжку (а, в), якому належать всі можливі значення Х, щільність розподілузберігає постійне значення, а поза проміжком дорівнює нулю, тобто

Графік рівномірного розподілу НВВ має вигляд:

Числові характеристики рівномірного закону розподілу:

· Математичне сподівання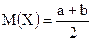

· Дисперсія

· Середньоквадратичне відхилення

Показниковий закон розподілу НВВ

Показниковим називають розподіл ймовірностей НВВ Х, що задається щільністю:

Графік показникового закону розподілу НВВ має вигляд:

Числові характеристики показникового закону розподілу:

· Математичне сподівання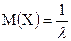

· Дисперсія

· Середньоквадратичне відхилення

Нормальний закон розподілу. Функція Лапласа.

Нормальним називають розподіл ймовірностей НВВ Х, щільністьроподілу якої має вигляд

де а – математичне сподівання

- середньоквадратичне відхилення

Графік нормального закону розподілу НВВ має вигляд:

Ймовірність того, що НВВ Х набуде значень, що належать проміжку 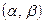дорівнює:

де - функція Лапласа

Наприклад: Математичне сподівання нормально розподіленої НВВ дорівнює а=3 і середньоквадратичне відхилення σ=2. Записати щільність розподілу Х.

Наприклад: Математичне сподівання та дисперсія нормально розподіленої ВВ Х відповідно дорівнюють 15 та 36. Обчислити ймовірність того, що в результаті випробування Х прийме значення, що належить проміжку від 10 до 22.

4. Біноміальний, геометричний та гіпергеометричний закони розподілу. Закон розподілу Пуассона

Біноміальний закон розподілу

Нехай проводиться n незалежних випробувань, в кожному з яких подія А може або з’явитися, або не з’явитися. Ймовірність появи у всіх випробуваннях постійна і дорівнює p.

Розглянемо в якості ДВВ Х – кількість появ події А в цих випробувань.

Можливі значення, які ДВВ може прийняти наступні:

х₁=0 – подія не з’явиться жодного разу

х₁=1 – подія з’явиться один раз....

х_п= п – подія з’явиться n раз

Ймовірності для цих подій обчислюються за формулою Бернуллі:

Формула Бернуллі і є аналітичним вираженням біноміального закону розподілу ДВВ.

Запишемо його вигляді таблиці:

X	n	n-1	…	k	…
P	p^n	np^n-1q	...		...	q^n

Приклад:

§ Гральний кубик підкинуто 3 рази. Записати закон випадіння шістки.

Геометричний закон розподілу

Нехай проводяться незалежні випробування, в кожному з яких ймовірність появи події А дорівнює р. Випробування закінчуються, як тільки з’явиться подія А.

В цьому випадку закон розподілу ДВВ визначається аналітичним виразом:

Р(Х)=q^k-1 ·p

Приклад: Підкидають монету. Випробування закінчується в тому випадку, коли з’явиться герб. Побудувати закон розподілу ДВВ випадіння герба.

3. Гіпергеометричний закон розподілу.

Нехай множина, яка складається з N елементів є підмножина з M елементів (M<N).Із множини N випадково відбирають n елементів, при чому кожен з ним може бути відібраний з однаковою ймовірністю і потім не повертається в множину. І нехай серед відібраних елементів n є m елементів, які належать підмножині M. Такий закон розподілу ДВВ Х – кількості m елементів серед n відібраних буде можна представити як

Приклад: В партії з 6 деталей є 4 стандартні. Навмання відібрані 2 деталі. Скласти закон розподілу кількості стандартних деталей серед відібраних.

Закон розподілу Пуассона.

Нехай проводиться n незалежних випробувань, в кожному з яких подія А може або з’явитися, або не з’явитися з однаковою ймовірністю р. Розглянемо в якості ДВВ Х – кількість появ події А в таких випробуваннях.

Якщо ймовірність появи події А у всіх випробуваннях дуже мала (p≤0,1), то ймовірності, що відповідають можливим значенням ДВВ Х обчислюється за формулою Пуассона

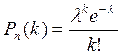, де = n·p

Тобто закон розподілу Пуассона показує ймовірності масових (п велике) та рідких (р - мала) подій.

Приклад: Магазин отримав 1000 пляшок мінеральної води. Ймовірність того, що під час транспортування пляшка виявиться розбитою, дорівнює 0,003. Побудувати закон розподілу цілочислової ДВВ Х – в дорозі розбилось не більше трьох пляшок.

Нехай проводиться n незалежних випробувань, при чому в першому випробуванні ймовірність появи події А дорівнює р₁, в другому - р₁,..., в n- му випробуванні – р_n.

Твірною функцією ймовірностей називають функцію, яка визначається рівністю:

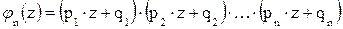
Ймовірність того, що в n незалежних випробуваннях в першому з яких ймовірність появи події А дорівнює р₁, в другому - р₁,..., в n- му випробуванні – р_n., подія А з’явиться рівно k разів, дорівнює коефіцієнту при р розкладенні твірної функції по степеням z.

Наприкладякщо п =2, то

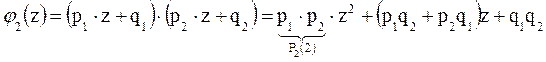
Приклад:

§ Два стрілки проводять по одному пострілу в ціль. Ймовірність влучення в ціль для першого стрілка дорівнює 0,7, а для другого – 0,9. Побудувати закон розподілу ДВВ Х – кількості влучень в ціль.

Питання для самоконтролю

1. Математичне сподівання, дисперсія, середнє квадратичне відхилення, їх властивості.

2. Моменти. Мода та медіана.

3. Рівномірний, показниковий та нормальний закони розподілу. Функція Лапласа

4. Біноміальний закон розподілу

5. Геометричний закон розподілу

6. Гіпергеометричний закон розподілу

7. Закон розподілу Пуассона

Тема 6. Багатовимірні випадкові величини

Лекція 6.

Закон розподілу двовимірних випадкових величин

Мета: сформувати знання щодо системи двох дискретних випадкових величин, її числових характеристик, законів розподілу, ймовірності попадання випадкової точки в півполосу, прямокутник.

План лекції:

1. Система двох дискретних випадкових величин та її закон розподілу

2. Функція розподілу двовимірної випадкової величини, ймовірність попадання в півполосу, прямокутник

3. Безумовні та умовні закони розподілу складових двовимірної дискретної випадкової величини

4. Умовне математичне сподівання. Регресія

Рекомендована література: [1] ст. 155-163, [4] ст. 120-128, [6] ст. 175-192

1. Система двох дискретних випадкових величин та її закон розподілу.

В попередніх лекціях було розглянуто випадкові величини, можливі значення яких визначались одним числом. Такі випадкові величини називають одномірними.

Але, при вивченні випадкових явищ в залежності від їх складності досить часто потрібно використовувати дві, три, а інколи, і більше випадкових величин.

Наприклад: Місце влучення снаряду визначається не одною, а двома ВВ – абсцисою та ординатою, розмір деталі – довжиною та шириною,....

Тобто, виникає необхідність переходу від одномірних випадкових величин до величин, можливі значення яких в кожному випробуванні визначаються 2, 3... числами. Такі величини називають багатомірними.

Обмежимось вивченням двовимірної випадкової величини.

Випадкова величина називається двовимірною, якщо всі її можливі значення мають вигляд ,при чому та

Законом розподілу двовимірної дискретної випадкової величини (ДДВВ) називають перелік можливих значень цієї величини та відповідних їм ймовірностей р

Звичайно такий закон задається у вигляді таблиці:

§ Приклад: Одночасно підкидають два гральних кубика. ВВ Х – парна сума очок, що випали на кубиках, ВВ Y – непарний добуток очок. Побудувати закон розподілу ВВ (X, Y).

2. Функція розподілу двовимірної випадкової величини. Ймовірність попадання випадкової точки в півполосу, прямокутник.

Функцією розподілу ДДВВ (Х, У) називають функцію F(Х, У), що визначає для кожної пари чисел х, у ймовірність того, що Х прийме значення менше ніж х і при цьому У прийме значення менше ніж у

F(Х, У)=Р(Х<x, Y<y)

§ Приклад: Знайти ймовірність того, що в результаті випробування складова Х ДВВ (Х,У) прийме значення Х<2 і при цьому складова У прийме значення У<3, якщо відома функція розподілу системи:

Геометрично функцію розподілу ДДВВ можна зобразити як ймовірність того, що точка потрапить в нескінчений квадрант

Властивості функції розподілу ДДВВ

1. ,

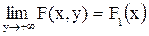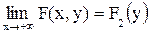
2.

3.

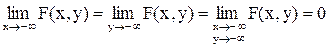
4. Ймовірність попадання випадкової точки в півполосу обчислюється за формулою:

4.1. якщо x₁<X<x₂, та Y<y, то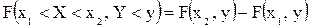

4.2. якщо x<X, та y₁<Y<y₂, то

5. Ймовірність попадання випадкової точки в прямокутник із сторонами, паралельними координатним осям, обчислюється за формулою:

3. Безумовні та умовні закони розподілу складових двовимірної ДВВ.

Безумовним законом розподілу складової Х н азивають сукупність можливих значень х₁, х₂, …,х_n та відповідних їм ймовірностейр(х₁), р(х₂), …, р(х_n)

Ймовірності р(х₁), р(х₂), …, р(х_n) обчислюють як

р(х₁)=р(х₁, у₁)+ р(х₁, у₂)+... +р(х₁, у_n)

р(х₂)=р(х₂, у₁)+ р(х₂, у₂)+... +р(х₂, у_n)

р(х_n)=р(х_n, у₁)+ р(х_n, у₂)+... +р(х_n, у_n)

Аналогічно

Безумовним законом розподілу складової Y н азивають сукупність можливих значень y₁, y₂, …,y_n та відповідних їм ймовірностейр(y₁), р(y₂), …, р(y_n)

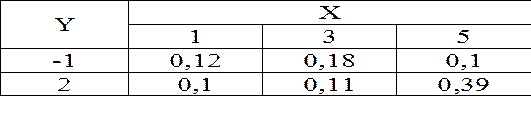Приклад: ДДВВ задано законом розподілу

Умовним законом розподілу складової Х якщо Y=y_j називають сукупність умовних ймовірностей р(х1│уj), р(х2│ уj) … р(хn│уj), які обчислюють за умови, що подія Y=y_j вже відбулася, тобто

р(х_i│у_j)= р(х_i, у_j)/ р(у_j)

Аналогічно

Умовним законом розподілу складової Y якщо X=x_i називають сукупність умовних ймовірностей р(y₁│x_i), р(y₂│ x_i) … р(y_n│x_i), які обчислюють за умови, що подія X=x_i вже відбулася, тобто

р (у_j│ х_i)= р(х_i, у_j)/ р(х_i)

Приклад: ДДВВ задано законом розподілу

Побудувати умовні закони розподілу складових ДДВВ

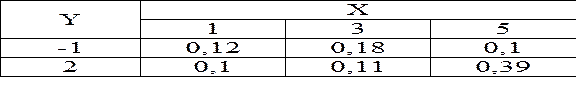4. Умовне математичне сподівання. Регресія.

Умовним математичним сподіванням ДДВВ Х, якщо Y=y називається сума добутків можливих значень X на їх умовні ймовірності

М(Х│У=у)=

Умовне математичне сподівання ДВВ Х, якщо Y=y є функцію від у, яку називають функцією регресії Х по Y.

Аналогічно

Умовним математичним сподіванням ДДВВ Y, якщо Х=х називається сума добутків можливих значень Y на їх умовні ймовірності

М(У│Х=х)=

Умовне математичне сподівання ДВВ Y, якщо X=x є функцію від x, яку називають функцією регресії Y по Х.

Приклад: ДДВВ задано законом розподілу

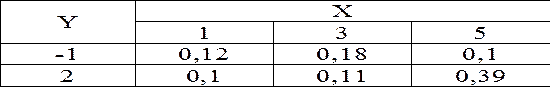Знайти регресію Х по У та У по Х

Розглянемо двовимірну ВВ (Х,У), закон розподілу якої відомий. В цьому випадку можна обчислити математичні сподівання та дисперсії складових Х та У. Однак ці числові характеристики не достатньо повно характеризують двовимірну ВВ (Х,У), так як не показують степені залежності її складових. Щоб більш точно охарактеризувати таку залежність використовують числову характеристику, яка називається кореляційним моментом або коваріцією.

Кореляційним моментом (коваріацією) К_ху випадкових величин Х і У називається математичне сподівання добутку відхилення цих величин від своїх математичних сподівань, тобто

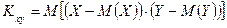
Кореляційний момент обчислюється за формулою:

- Для дискретних випадкових величин:

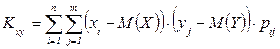
- Для неперервних випадкових величин:

Кореляційний момент двох ВВ характеризує як ступінь залежності ВВ так їх розсіювання навколо точки (М(Х), М(У)).

Властивості коефіцієнта кореляції:

1. Кореляційний момент двох незалежних випадкових величин дорівнює нулю.

2. Кореляційний момент двох випадкових величин дорівнює математичному сподіванню їх добутку мінус добуток їх математичних сподівань:

3. Кореляційний момент двох ВВ по абсолютній величині не перебільшує добутку їх середньоквадратичних відхилень:

Оскільки кореляційний момент – величина, що має розмірність, що визначається добутком розмірностей випадкових величин, то це ускладнює використання кореляційного моменту для оцінки ступеню залежності для різних випадкових величин. Для виключення цього недоліку використовують коефіцієнт кореляції.

Коефіцієнтом кореляції двох випадкових величин називається відношення їх кореляційного моменту до добутку середньоквадратичних відхилень цих величин. (отже коефіцієнт кореляції – величина безрозмірна)

Властивості коефіцієнту кореляції:

1. Коефіцієнт кореляції приймає значення на відрізку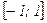

2. Якщо випадкові величини незалежні, то їх коефіцієнт кореляції дорівнює нулю.

Якщо коефіцієнт кореляції двох випадкових величин по абсолютній величині дорівнює одиниці, то між цими випадковими величинами існує лінійна функціональна залежність

Приклад: ДДВВ задано законом розподілу

Знайти кореляційний момент та коефіцієнт кореляції

Питання для самопідготовки

1. Система двох дискретних випадкових величин та її закон розподілу

2. Функція розподілу двовимірної випадкової величини, ймовірність попадання в півполосу, прямокутник

3. Безумовні та умовні закони розподілу складових двовимірної дискретної випадкової величини

4. Умовне математичне сподівання. Регресія

Тема 9. Елементи теорії випадкових процесів і теорії масового обслуговування

Лекція 7.

Елементи теорії випадкових процесів та теорії масового обслуговування

Мета: сформувати знання з теорії випадкових процесів: основні означення, числові характеристики, властивості, ввести поняття марківського процесу та поняття перехідних ймовірностей; сформувати знання з основ теорії масового обслуговування: основні поняття та класифікація систем масового обслуговування, одноканальна та багатоканальна системи масового обслуговування з відмовленнями

План лекції:

1. Означення випадкового процесу

2. Потоки подій та їх властивості

3. Марківські процеси

4. Основні поняття та класифікація систем масового обслуговування

5. Одноканальна система масового обслуговування з відмовленнями

6. Багатоканальна система масового обслуговування з відмовленнями. Задача Ерланга

Рекомендована література: [1] ст. 131-140, [4] ст. 137-135, [6] ст. 135-145

Теорія випадкових процесів спрямована на розв’язання 2 основних видів задач:

1. Якщо задано параметри та імовірнісні характеристики на вході випадкового процесу і необхідно дослідити, якими будуть ці параметри та характеристики по закінченню випадкового процесу (на виході)

2. задано характеристики та параметри на виході з випадкового процесу і необхідно створити модель оптимальної системи, яка б гарантувала задані характеристики

Випадковим процесом Х(t) називають процес, значення якого при будь – якому значенні аргументу t є величиною випадковою.

Тобто ВП – це функція, яка в результаті випробування може прийняти той чи інший, наперед невідомий вигляд

Для будь – якого конкретного значення t= t₀, Х(t₀) представляє собою звичайну випадкову величину, що носить назву розріз

Реалізацією (траєкторією) ВП називається невипадкова функція х(t), в яку перетворюється ВП Х(t) в результаті випробування.

Таким чином, ВП можна розглядати як сукупність ВВ {Х(t)}, що залежать від параметру t або як сукупність її можливих реалізацій.

Числові характеристики ВП:

1. Математичним сподіванням ВП Х(t) називають невипадкову функцію m_x(t), значення якої при кожному фіксованому значенні аргументу дорівнює математичному сподіванню розрізу, що відповідає тому самому фіксованому значенню аргументу.

m_x(t)=М[Х(t)]

2. Дисперсією ВП Х(t) називають невипадкову невід’ємну функцію D_x(t), значення якої при кожному фіксованому значенні аргументу дорівнює дисперсії розрізу, що відповідає тому самому фіксованому значенню аргументу

D_x(t)= D(Х(t))

Кореляційною функцією ВП Х(t) називають невипадкову функцію К_х(t _1,t₂) двох незалежних аргументів t _1,t_2, значення якої при кожній парі фіксованих значень аргументів дорівнює кореляційному моменту розрізів, що відповідають тим самим фіксованим значенням аргументів

К_x(t₁, t₂)=M[(Х(t₁)- m_x(t₁))*(Х(t₂)- m_x(t₂))]

2. Потоки подій та їх властивості.

Потоком подій називають послідовність однорідних подій, що відбуваються одна за одною в деякі випадкові моменти часу.

Потоки подій характеризуються інтенсивністю λ – частотою появи подій або середньою кількістю подій, що відбуваються в одиницю часу.

Потік подій називають регулярним, якщо події відбуваються одна за одною через відповідні рівні проміжки часу.

Потік подій називають стаціонарним, якщо його імовірнісні характеристики не залежать від часу (тобто λ =const)

Потік подій називається потоком без наслідків, якщо для будь – яких двох періодів часу, що не перетинаються, кількість подій, що потрапляє на один з них, не залежить від кількості подій, що потрапляють на інші.

Поток подій називається ординарним, якщо ймовірністю попадання в малий період часу двох або більше подій можна знехтувати у порівнянні з ймовірністю попадання одної події.

Потік подій називається найпростішим (пуассоновським), якщо він одночасно стаціонарний, ординарний і не має наслідків.

Можна довести, що якщо постійна інтенсивність потоку відома, то ймовірність появи k подій за час t визначається за формулою Пуассона, де

=np

3. Марківські процеси.

Процес називається процесом з дискретними станами, якщо його можливі стани s₁, s₂, s3…можна перерахувати, а перехід системи з одного стану до іншого відбувається миттєво (скачком)

Процес називається процесом із неперервним часом, якщо моменти можливих переходів системи із стану в стан наперед не фіксовані, а випадкові.

Будемо розглядати випадкові процеси з дискретними станами та неперервним часом.

ВП називають марківським (випадковим процесом без наслідків), якщо для будь – якого моменту часу t₀ ймовірнісні характеристики процеса в майбутньому залежать тільки від його стану в даний момент t₀ і не залежать від того, коли і як система прийшла в даний стан.

Ланцюг Маркова – це послідовність випробувань, в кожному з яких з’являється тільки одна з несумісних подій А₁, А₂,…, Ак, що складають повну групу, при чому умовна ймовірність p_ij(s), того що в s-тому випробуванні наступить подія А_j за умови, що в (s-1)-му випробуванні наступила подія А_i, не залежить від результатів попередніх випробувань.

Однорідним називають ланцюг Маркова, якщо умовна ймовірність p_ij(s) (переходу із стану I в стан j) не залежить від номеру стану s і записується ця ймовірність як p_ij

Перехідною ймовірністю p_ij називають умовну ймовірністьтого, що із стану i (в якому система опинилася в результаті деякого випробування) в результаті наступного випробування система перейде в стан j

Нехай кількість станів кінцева і дорівнює к

Матрицею переходу системи називають матрицю, що включає в себе всі перехідні ймовірності даної системи.

P₁=

Можна довести, матриця переходу системи із одного стану в інший за m кроків обчислюється за формулою:

4. Основні поняття та класифікація систем масового обслуговування.

На практиці досить часто зустрічаються системи, що призначені для багаторазового використання під час розв’язку однотипних задач.

Процеси, що відбуваються при цьому отримали назву процесів обслуговування, а системи, що виконують однотипні задачі – систем масового обслуговування

Кожна така система складається з певної кількості елементів обслуговування, що мають назву каналів обслуговування.

По кількості каналів обслуговування СМО поділяються на одно канальні та багатоканальні.

Оскільки заявки потрапляють в СМО нерівномірно, а випадково, утворюючи випадковий потік заявок, а, також, обслуговування заявок продовжується деякий випадковий проміжок часу, то СМО виявляється завантаженою нерівномірно.

Тому в деякі моменти часу СМО виявляється пере завантаженою і заявки або становляться в чергу, або покидають систему, або, навпаки, система не завантажена та простоює.

Предметом теорії масового обслуговування є побудова математичних моделей, що поєднують задані умови роботи СМО (кількість каналів, їх виробничість...) з показниками ефективності СМО, що характеризуються її здатністю обслуговувати потік заявок.

В якості показників ефективності СМО використовуються:

- Середня кількість заявок, що обслуговуються в одиницю часу;

- Середня кількість заявок в черзі;

- Середній час очікування обслуговування;

- Ймовірність того, що кількість заявок в черзі буде перевищувати певне значення і т.д.

СМО поділяють на 2 типи:

1. СМО з відмовами – заявка, що потрапила в систему в час, коли всі канали зайняті, отримує відмову і покидає СМО не обслугованою.

2. СМО с очікуванням – заявка, що потрапила в систему в час, коли всі канали зайняті, не покидає систему, а становиться в чергу на обслуговування.

Процес роботи СМО представляє собою випадковий процес з дискретними станами та неперервним часом. Отже для геометричного представлення даних процесів зручно користуватися графами станів.

5. Одноканальна система масового обслуговування з відмовленнями.

СМО з відмовленнями представляє собою випадковий процес, що має назву процесу загибелі та розмноження.

Граф станів даного процесу представлено на рис.

В якості показників ефективності СМО з відмовленнями розглянемо:

q А – абсолютну пропускну здібність (середню кількість заявок, що обслуговуються в одиницю часу)

q Q – відносну пропускну здібність (середню долю заявок, що обслуговує система)

q Р_відм – ймовірність відмови (ймовірність того, що заявка покине СМО не обслуженою)

Гранична ймовірність стану S_i вказує на середній час перебування системи в цьому стані.

Знайти граничні ймовірності можна за правилом:

Граничні ймовірності р_і знаходяться з системи рівнянь, в якій зліва в рівняннях стоїть гранична ймовірність, помножена на суму інтенсивностей всіх потоків, що виходять з даного стану, а справа – сума добутків інтенсивностей всіх потоків, що входять в даний стан, на ймовірності тих станів, з яких ці потоки виходять.

Розглянемо одноканальную систему с відмовленнями:

Маємо один канал, на який надходить потік заявок з інтенсивністю λ.

Потік обслуговувань має інтенсивність μ.

Необхідно знайти граничні ймовірності станів системи та показники її ефективності.

Система може мати 2 стани:

q Канал вільний

q Канал зайнятий.

Для знаходження граничних ймовірностей складають систему:

Отже ,

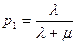
Так як р₀ – виражає середній відносний час перебування системи в стані S₀ – коли канал вільний, то вона визначає відносну пропускну здатність системи

Р₁ - гранична ймовірність того, що канал зайнятий (стан S₁) – відповідно це ймовірність відмови

Абсолютну пропускну здатність знайдемо помноживши відносну пропускну здатність Q на інтенсивність потока заявок λ

6. Багатоканальна система с відмовленнями (задача Эрланга)

Розглянемо систему, яка має n каналів, на які надходить потік заявок з інтенсивністю λ. Потік обслуговувань кожного канала має інтенсивність μ. Необхідно знайти граничні ймовірності станів системи та показники її ефективності.

Система має стани з номерами, що відповідають кількості заявок, що знаходяться в системі (S₀ – жодної заявки, S₁ – одна, тобто зайнятий 1 канал і т. д.)

Граф станів відповідає процесу загибелі та розмноження

Запишемо формулу для обчислення граничних ймовірностей системи:

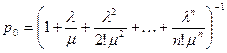де - приведена інтенсивність навантаження отже

…

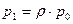
- формули Ерланга

Ймовірність відмови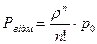

Відносна пропускна здатність

Абсолютна пропускна здатність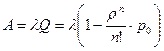

Введемо ще одну характеристику ефективності системи: –

Середню кількість зайнятих каналів:

де p_k – граничні ймовірності станів

Прикл. Відомо, що заявки в телеательє надходять з інтенсивністю λ=90 заявок в год, а середня тривалість розмови по телефону =2 хв. Визначити

q показники ефективності СМО за наявності 1 телефонного номера

q оптимальну кількість телефонних номерів, якщо умовою оптимальності вважати задоволення з кожних 100 заявок в средньому не менше 90 заявок.

Питання для самопідготовки

1. Означення випадкового процесу

2. Потоки подій та їх властивості

3. Марківські процеси

4. Основні поняття та класифікація систем масового обслуговування.

5. Одноканальна система масового обслуговування з відмовленнями.

6. Багатоканальна система масового обслуговування з відмовленнями. Задача Ерланга

Дата добавления: 2017-02-01