
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комплексные числа
|
|
|
|
Алгебраические многочлены и дробно-рациональные функции.
Мнимая единица − это  (imaginary). Так как
(imaginary). Так как 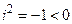 , то
, то  не может быть действительным числом. Комплексным числом называется сумма вида
не может быть действительным числом. Комплексным числом называется сумма вида 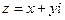 , где
, где 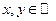 . Число
. Число  называется действительной частью
называется действительной частью  , число
, число  называется мнимой частью
называется мнимой частью  . Записывается это так:
. Записывается это так:  . Ещё раз подчёркиваем, что
. Ещё раз подчёркиваем, что  (как и
(как и  ) ― действительное число. Вводя на множестве комплексных чисел обычные операции сложения и умножения, получаем поле комплексных чисел
) ― действительное число. Вводя на множестве комплексных чисел обычные операции сложения и умножения, получаем поле комплексных чисел 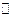 .
.

| Поставим в соответствие комплексному числу 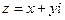 точку с декартовыми координатами точку с декартовыми координатами 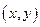 . Полярные координаты этой же точки обозначим . Полярные координаты этой же точки обозначим 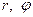 . В таком случае . В таком случае  . Поэтому . Поэтому  . Ясно, что . Ясно, что 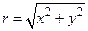 .
В отличие от алгебраической записи .
В отличие от алгебраической записи 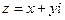 , равенство , равенство  называется тригонометрической записью комплексного числа называется тригонометрической записью комплексного числа  . Число . Число 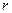 называют модулем называют модулем  , число , число 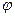 − аргументом − аргументом  ; их обозначения: ; их обозначения:  . .
|
Число 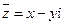 называют сопряженным к числу
называют сопряженным к числу 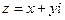 . Ясно, что
. Ясно, что 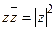 .
.
Операции в поле 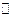 .
.
Если 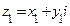 ,
,  , то
, то 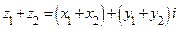 , а
, а  . Впрочем, перемножать комплексные числа удобнее, если использовать их тригонометрическую запись. Действительно,
. Впрочем, перемножать комплексные числа удобнее, если использовать их тригонометрическую запись. Действительно,

 .
.
Таким образом, при перемножении комплексных чисел их модули перемножаются, а их аргументы складываются. Это подсказывает еще одну форму записи комплексных чисел − показательную или экспоненциальную: 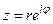 . Более естественное обоснование формул Эйлера
. Более естественное обоснование формул Эйлера
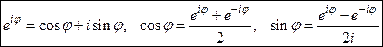 ,
,
связывающих показательную функцию и тригонометрические функции, будет дано
в теории степенных рядов.
Отметим свойства операции сопряжения:  ,
, 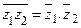 ,
,  .
.
2˚. Алгебраические многочлены. Мы будем рассматривать алгебраические многочлены 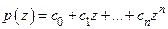 , зависящие от комплексной переменной
, зависящие от комплексной переменной  , с комплексными
, с комплексными
коэффициентами  .
.
Теорема Гаусса (О сновная теорема алгебры). Алгебраический многочлен  степени
степени  имеет ровно
имеет ровно 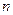 (комплексных) корней с учетом их кратности.
(комплексных) корней с учетом их кратности.
|
|
|
Это означает, что существует разложение 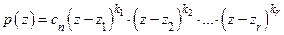 .
.
Здесь  − попарно различные корни многочлена, а натуральные числа
− попарно различные корни многочлена, а натуральные числа 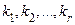 − кратности этих корней. Ясно, что
− кратности этих корней. Ясно, что 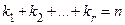 .
.
Следствие 1. Пусть известно, что все коэффициенты многочлена  − действительные числа. В таком случае, если число
− действительные числа. В таком случае, если число  является корнем
является корнем  кратности
кратности 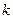 , то
, то 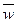 также −
также − 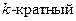 корень этого многочлена.
корень этого многочлена.
Доказательство*. Имеем  , так как
, так как  − действительные числа. Следовательно,
− действительные числа. Следовательно,
 Следствие 2. Многочлен с действительными коэффициентами разлагается на линейные и квадратичные множители с действительными коэффициентами.
Следствие 2. Многочлен с действительными коэффициентами разлагается на линейные и квадратичные множители с действительными коэффициентами.
Это вытекает из того, что 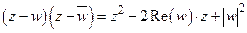 .
.
3˚. Дробно-рациональные функции. Рациональной дробью называется отношение двух алгебраических многочленов. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. В противном случае дробь − неправильная. Деля числитель дроби на знаменатель, можно превратить неправильную дробь в сумму многочлена и правильной дроби. Поэтому, для того, чтобы суметь проинтегрировать любую рациональную функцию нужно научиться интегрировать правильные дроби. Для этого нам потребуется умение разбить правильную дробь на простые дроби и умение интегрировать простые дроби. Начнем с определения.
Определение. Дробь называется простой, если её знаменатель представляет собой линейную или квадратичную скобку в натуральной степени, а степень числителя на единицу, меньше чем степень многочлена, стоящего внутри этой скобки.
Теорема. Правильная дробь 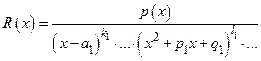 с действительными коэффициентами единственным способом может быть представлена в виде суммы простых дробей. Здесь каждой скобке в разложении знаменателя отвечает группа простых дробей, содержащих в знаменателях эту скобку в степенях от первой до той, с которой скобка входит в разложение знаменателе исходной дроби.
с действительными коэффициентами единственным способом может быть представлена в виде суммы простых дробей. Здесь каждой скобке в разложении знаменателя отвечает группа простых дробей, содержащих в знаменателях эту скобку в степенях от первой до той, с которой скобка входит в разложение знаменателе исходной дроби.
|
|
|
Пусть, например,  . Тогда знаменатель можно разложить на множители минимальной степени
. Тогда знаменатель можно разложить на множители минимальной степени  =
= . Поэтому
. Поэтому 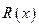 разбивается на простые дроби следующим образом:
разбивается на простые дроби следующим образом: 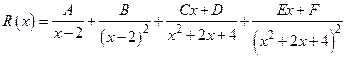 . Для нахождения значений
. Для нахождения значений  обычно используют метод неопределенных коэффициентов. Мы обсудим этот прием при рассмотрении последующих примеров.
обычно используют метод неопределенных коэффициентов. Мы обсудим этот прием при рассмотрении последующих примеров.
Доказательство теоремы легко получить с помощью следующих двух лемм.
Лемма 1. Пусть  − многочлены с действительными коэффициентами,
− многочлены с действительными коэффициентами, 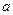 − действительное число, причем
− действительное число, причем  и
и  N. Существует единственное действительное число
N. Существует единственное действительное число 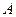 и многочлен с действительными коэффициентами
и многочлен с действительными коэффициентами  такие, что выполняется тождество
такие, что выполняется тождество
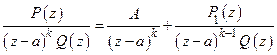 .
.
Доказательство леммы 1. Рассмотрим разность
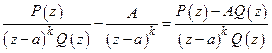 .
.
Многочлен  делится на двучлен
делится на двучлен  тогда и только тогда, когда
тогда и только тогда, когда 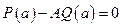 , т.е.
, т.е.  , так как
, так как  .
.
Лемма 2. Пусть  − многочлены с действительными коэффициентами,
− многочлены с действительными коэффициентами, 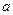 − комплексное число
− комплексное число 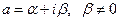 ,
, 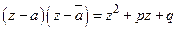 . Пусть еще известно, что
. Пусть еще известно, что  (иначе говоря,
(иначе говоря, 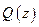 не делится
не делится 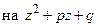 ) и что
) и что 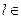 N. Тогда существует единственная пара действительных чисел
N. Тогда существует единственная пара действительных чисел 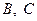 и многочлен с действительными коэффициентами
и многочлен с действительными коэффициентами  , такие что
, такие что
 .
.
Доказательство леммы 2. Рассмотрим разность
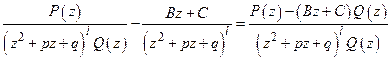 .
.
Числитель последней дроби делится на квадратный трехчлен  тогда и только тогда, когда
тогда и только тогда, когда 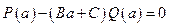 или
или 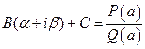 . Последнее отношение определено, так как
. Последнее отношение определено, так как  . Запишем это отношение в виде
. Запишем это отношение в виде 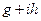 . Тогда для нахождения чисел
. Тогда для нахождения чисел 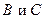 получим линейную систему с действительными коэффициентами:
получим линейную систему с действительными коэффициентами:  . Эта система имеет единственное (действительное) решение
. Эта система имеет единственное (действительное) решение  , так её определитель
, так её определитель 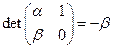 по условию отличен от нуля.
по условию отличен от нуля.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 487; Нарушение авторских прав?; Мы поможем в написании вашей работы!