Два определения интеграла Римана

Глава 6.Определенный интеграл и его приложения. Несобственные интегралы.

Случаи интегрируемости дифференциального бинома.

Дифференциальный бином − это выражение вида 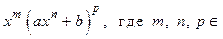Q.

1-й случай: 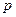− целое; замена 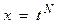, где − НОК знаменателей чисел .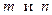

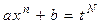2-й случай: − целое; замена , где 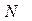− знаменатель числа .

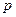3-й случай: 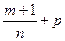− целое; замена , где 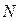− знаменатель числа .

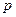П.Л. Чебышёв доказал, что во всех других случаях интеграл

не является элементарной функцией.

§1. Задачи, приводящие к понятию определённого интеграла.

1. Задача о площади (или о квадратуре) криволинейной трапеции. Пусть 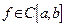− положительная функция. Требуется найти площадь 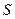фигуры, ограниченной графиком этой функции, осью абсцисс, и отрезками .

Если 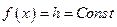, то . В общем случае это произведение зависит 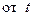. Оно даёт 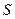с ошибкой, доходящей . Здесь − колебание функции на отрезке 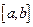, т.е. 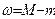, где 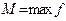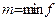(Рис 1).

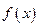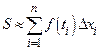Для того, чтобы учесть изменение функции , разобьём отрезок на частичные отрезки , выберем . Тогда получим . Ошибка сейчас не превышает суммы площадей заштрихованных фигур на рисунке 2, что значительно меньше, чем прежде.

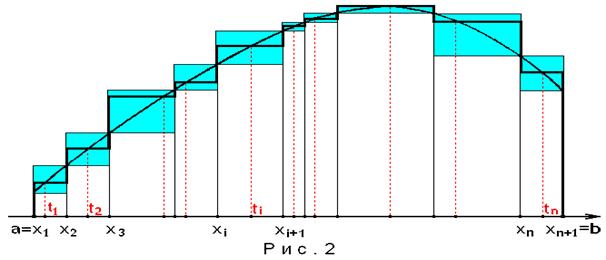
Так как непрерывная функция мало изменяется при малых изменениях аргумента, то, по-видимому, точное значение площади равно

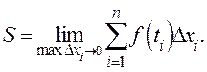
2. Та же конструкция возникает при вычислении перемещения точки, если известна её скорость.

3. Тот же предел суммы приходится рассматривать в задаче о нахождении массы (или заряда) стержня по известной линейной плотности массы (заряда) и т.д. и т.п.

1˚. Пусть ; 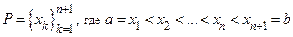− разбиение отрезка . Пусть далее 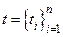− набор промежуточных точек, согласованный с разбиением 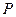, т.е. ; 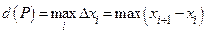− мелкость разбиения .

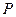Наконец, будет обозначать множество всех таких наборов 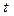, согласованных .

Определение 1. Мы будем называть 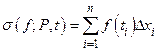римановой интегральной суммой для функции , соответствующей разбиению 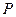и набору .

Определение 2. Число называется пределом интегральных сумм при условии, что мелкость разбиения стремится к нулю (в записи 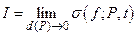), если для любого числа 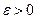найдется такое число 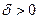, что при любых 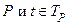, для которых , выполняется неравенство .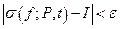

Первое основное определение. Функция называется интегрируемой по Риману на отрезке или короче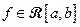, если существует предел 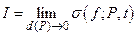. Сам предел называется определённым интегралом Римана и обозначается .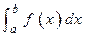

Отметим, что название “интеграл” происходит от “integer” − целый, а обозначение 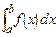подчеркивает происхождение из суммы 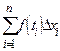(стилизованная буква S).

Теорема. (Необходимое условие интегрируемости). Если функция интегрируема на отрезке , то она ограничена на этом отрезке.

Доказательство. Предположим, что функция 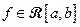, но не является ограниченной. Существует число 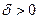, такое что будет .

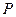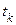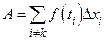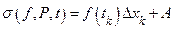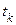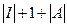Фиксируем разбиение , для которого . Так как функция неограниченна на отрезке , то она неограниченна на некоторых частичных отрезках, скажем . Фиксируем все , , а само оставим пока неопределённым. Если обозначить , то получим . Выберем теперь значение так, чтобы было больше, чем . Тогда окажется, что . А это противоречит выбору числа .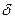

2˚. Дальше мы будем рассматривать только ограниченные функции. Для каждой такой

функции и разбиения 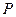можно определить величины:

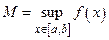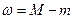, , − колебание функции на отрезке , а для частичных отрезков разбиения 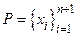полагаем , , .

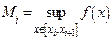Дата добавления: 2013-12-13