Доверительный интервал для математического ожидания при неизвестной дисперсии. Распределение Стьюдента

В предыдущем параграфе для построения доверительного интервала была введена центрированная нормированная случайная величина U

.

Величина называется центрированной, если она получена путём вычитания из исходной случайной величины её математического ожидания a. Математическое ожидание центрированной случайной величины равно нулю (см. свойство математического ожидания № 5). Величина называется нормированной, если производится деление на генеральное среднеквадратическое отклонение среднего значения.

Но значение среднеквадратического отклонения генеральной совокупности 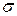чаще всего неизвестно, и приходиться в качестве её оценки использовать выборочное среднеквадратическое отклонение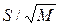

Поэтому, взамен случайной величины U вводится случайная величина t равная

. (4.43)

Эта случайная величина имеет функцию плотности распределения вероятности, которая называется распределением Стьюдента и рассчитывается по формуле

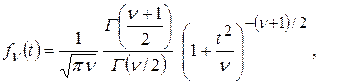(4.44)

где величина ν = M − 1, называется числом степеней свободы (величина, возникающая в процессе расчёта выборочного среднеквадратического отклонения S), а Г(η) − специальная математическая функция (гамма − функция).

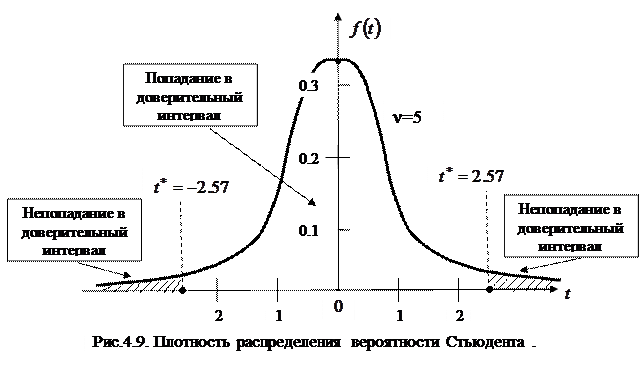
Задав число степеней свободы можно вычислить плотность распределения вероятности по формуле (4.44). На рис. 4.9. представлена плотность распределения при ν = 5.

Для построения доверительных интервалов используют таблицу коэффициентов Стьюдента, фрагмент которой представлен в таблице 4.8. В таблице приведены значения коэффициентов Стьюдента в зависимости от заданной доверительной вероятности и числа степеней свободы ν. Индекс γ показывает, что коэффициентов Стьюдента зависит от выбранного значения доверительной вероятности. В первой строке таблицы указаны эти значения доверительной вероятности γ = (1– α), которые принимают значения (0.5,….0.98, 0.99). В первом столбце указаны значения числа степеней свободы ν (1, 2, 3, 4,…24). При выполнении измерений обычно задаются доверительной вероятностью 0.90 или 0,95.

Рассмотрим принцип получения таблицы. В основе её построения лежит выражение

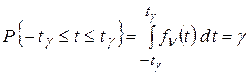, (4.45)

Таблица 4.8

ν	Доверительная вероятность, γ = 1 – α
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99
	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
	0,82	1,06	1,34	1,89	2,92	4,30	6,97	9,93
	0,77	0,98	1,25	1,64	2,35	3,18	4,54	5,84
	0,74	0,94	1,19	1,53	2,13	2,78	3,75	4,60
	0,73	0,92	1,16	1,48	2,02	2,57	3,37	4,03
	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
	0,71	0,90	1,12	1,42	1,90	2,37	3,00	3,50
	0,71	0,89	1,11	1,40	1,86	2,31	2,90	3,36
	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
	0,69	0,86	1,06	1,32	1,71	2,06	2,49	2,80

которое означает следующее – доверительная вероятность события, заключающегося в том, что случайная переменная t попадёт в интервал от t_γ до − t_γ равна интегралу от плотности распределения вероятности Стьюдента. Допустим, что требуется найти доверительный интервал с доверительной вероятностью 95 % (γ = 0.95), а число степеней свободы равно 5. Тогда

Из последнего интегрального равенства, зная вид распределения Стьюдента (4.44), можно найти предел интегрирования t_γ, который и является коэффициентом Стьюдента. В данном случае t_γ = 2.57, это число помещается на пересечении столбца γ = 0.95 и строки ν = 5.

Таким образом, статистический смысл коэффициента t_γ в том, что он показывает половину доверительного интервала

.

Геометрически, площадь под криволинейной фигурой, ограниченной вертикалями t_γ = 2.57 и t_γ = – 2.57, показывает вероятность попадания случайной величины в указанный интервал. Площадь равна 0.95 (см. рис.4.9) Площадь заштрихованной фигуры левее линии t_γ = – 2.57 показывает вероятность непопадания в этот интервал и равна 0.025. Площадь заштрихованной фигуры правее линии t_γ = 2.57 тоже показывает вероятность непопадания и тоже равна 0. 025. Следовательно, суммарная вероятность непопадания случайной величины t в интервал от – 2.57 до 2.57 равна (0.025+ 0.025) = 0.05.

Раскроем величину t по формуле (4.43) и подставим вместо t в выражение (4.43)

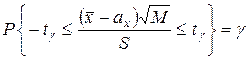. (4.46)

Путём простых преобразований в скобках, перейдём к неравенствам для математического ожидания a

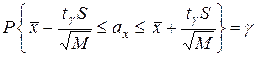. (4.47)

Двойное неравенство в фигурных скобках является искомым доверительным интервалом для математического ожидания a_x.

Таким образом, алгоритм нахождения доверительного интервала для математического ожидания в случае, когда генеральная дисперсия σ² неизвестна, состоит из следующих этапов:

1) Производят М измерений случайной величины Х, то есть производят выборку (x₁,x₂, x₃, ….. x_M) из генеральной совокупности,

2) Рассчитывают выборочное среднее (которое является оценкой математического ожидания a_x генеральной совокупности) по формуле (4.21),

3) Рассчитывают выборочное среднеквадратическое отклонения S (являющееся оценкой генерального среднеквадратического отклонения σ) по формуле (4.26) и определяют число степеней свободы ν = (М – 1),

4) Задают доверительную вероятность γ, она указывает, с какой достоверностью можно пользоваться полученным доверительным интервалом,

5) Используя число степеней свободы ν и доверительную вероятность γ, по таблице находят коэффициент Стьюдента t_γ,

6) Находят доверительный интервал по формуле (4.47).

В качестве примера, [Химмельблау] определим доверительный интервал для математического ожидания при измерении массы некоторого количества образцов. Пусть из всей партии выбрано 8 образцов и произведено их взвешивание. Результаты представлены в таблице 4.9.

Таблице 4.9

Номер образца
Масса, г	76.48	76.43	77.20	76.45	76.25	76.48	76.48	76.60

Среднее значение равно .

Выборочная дисперсия равна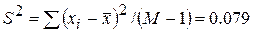

Пусть доверительный интервал определяется с вероятностью γ = 95%. При этой доверительной вероятности и числе степеней свободы ν = (8 – 1) = 7. находим по таблице коэффициент Стьюдента t_γ = 2.37. Найдём выборочное среднеквадратическое отклонения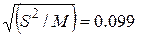. Рассчитаем доверительный интервал

76.55 – 0.099 2.37 < a < 76.55 + 0.099 2.37

76.31 < a_x < 76.79

Вывод: с вероятностью 95 % можно утверждать, что математическое ожидание (истинное среднее значение) веса по всей партии образцов лежит в интервале от 76.31 до 76.79 грамм.

Дата добавления: 2013-12-13