Приближение функции многочленами Тейлора

Постановка задачи

Тема 4. Приближение функций

Задача приближения (аппроксимации) функций заключается в том, чтобы для данной функции построить другую, отличную от нее функцию, значения которой достаточно близки к значениям данной функции. Такая задача возникает на практике достаточно часто. Укажем наиболее типичные случаи.

1. Функция задана таблицей в конечном множестве точек, а вычисления нужно произвести в других точках.

2. Функция задана аналитически, но ее вычисление по формуле затруднительно.

При решении задачи поиска приближенной функции возникают следующие проблемы.

1. Необходимо выбрать вид приближенной функции. Для приближения широко используются многочлены, тригонометрические функции, показательные функции и т. д.

2. Необходимо выбрать критерий близости исходной и приближенной функции. Это может быть требование совпадения обеих функций в узловых точках (задача интерполяции), минимизация среднеквадратического уклонения (метод наименьших квадратов) и др.

3. Необходимо указать правило (алгоритм), позволяющее с заданной точностью найти приближение функции.

Пусть функция y = f (x) определена в окрестности точки a и имеет в этой окрестности n + 1 производную. Тогда в этой окрестности справедлива формула Тейлора:

f (x) = c ₀ + c ₁(x – a) + c ₂(x – a)² + … + c_n (x – a) ⁿ + R_n (x) = T_n (x) + R_n (x),

где c_k =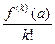

T_n (x) – многочлен Тейлора:

T_n (x) = c ₀ + c ₁(x – a) + c ₂(x – a)² + … + c_n (x – a) ⁿ, (4.1)

R_n (x) – остаточный член формулы Тейлора. Его можно записать различными способами, например, в форме Лагранжа:

R_n (x) = 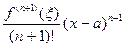, a £ x £ x.

Многочлен Тейлора (4.1) обладает свойством, что в точке x = a все его производные до порядка n включительно совпадают с соответствующими производными функции f, т. е.

T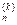 (a) = f ^{( k )}(a), k = 0, 1, …, n.

В этом легко убедиться, дифференцируя T_n (x). Благодаря этому свойству многочлен Тейлора хорошо приближает функцию f в окрестности точки a. Погрешность приближения составляет

| f (x) – T_n (x)| = | R_n (x)|,

т. е. задавая некоторую точность e > 0, можно определить окрестность точки a и значение n из условия:

| R_n (x)| = 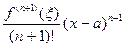< e. (4.2)

Пример 4.1.

Найдем приближение функции y = sinx многочленом Тейлора в окрестности точки a = 0. Воспользуемся известным выражением для k -ой производной функции sinx:

(sinx)^(k) = sin x + k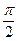 (4.3)

Применяя последовательно формулу (4.3), получим:

f (0) = sin 0 = 0;

f ' (0) = cos (0) = 1;

f" (0) = –sin 0 = 0;

f ^{(2 k- 1)}(0) = sin (2 k – 1) 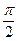= (–1) ^{k – 1} ;

f ^{(2 k )}(0) = 0;

f ^{(2 k+ 1)}(x) = (–1) ^kcosx.

Следовательно, многочлен Тейлора для функции y = sinx для n = 2 k имеет вид:

sinx = x – 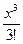+ … + (– 1) ^{k – 1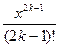} + R _{2 k} (x),

R _{2 k} (x) = (– 1) ^k .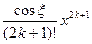

Зададим e = 10 ^–4 и отрезок [ –, ]. Определим n = 2 k из неравенства:

| R _{2 k} (x)| = 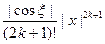< < 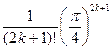< 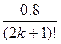e = 10^-4.

Таким образом, на отрезке –, функция y = sinx с точностью до e = 10^-4 равна многочлену 5-ой степени:

sinx = x – 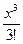+ 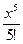= x – 0.1667 x ³ + 0.0083 x ⁵.

Пример 4.2.

Найдем приближение функции y = e^x многочленом Тейлора на отрезке [0, 1] с точностью e = 10 ^–5.

Выберем a = ½, т. е в середине отрезка. При этом величина погрешности в левой части (4.2) принимает минимальное значение. Из математического анализа известно, что для k -ой производной от e^x справедливо равенство:

(e^x)^(k) = e^x.

Поэтому

(e^a)^(k) = e^a = e ^{1 / 2},

Следовательно, многочлен Тейлора для функции y = e^x имеет вид:

e^x = e ^{1 / 2 +} e ^{1 / 2}(x – ½) + (x – ½)² + … + 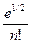(x – ½)ⁿ + R_n (x),

При этом, учитывая, что x Î [0, 1], получим оценку погрешности:

| R_n (x)| < 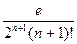. (4.4)

Составим таблицу погрешностей, вычисленных по формуле (4.4):

n
Rn	0.057	0.0071	0.00071	0.000059	0.0000043

Таким образом, следует взять n = 6.

Дата добавления: 2014-01-05