Правила дифференцирования

ТЕМА 5. ПРОИЗВОДНАЯ.

Задача о касательной.

Схема вычисления производной.

1. ЗАДАЧА О КАСАТЕЛЬНОЙ

Пусть на плоскости 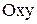дана непрерывная кривая 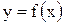и необходимо найти уравнение к этой кривой в точке .

Дадим аргументу 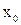приращение 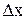и перейдем на кривой 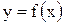от точки 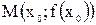к точке . Проведем секущую .

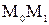Под касательной к кривой 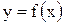в точке 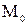естественно понимать предельное положение секущей 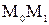при приближении точки 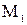к точке 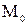, т.е. при .

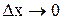Уравнение прямой, проходящей через точку 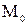имеет вид:

.

Угловой коэффициент (или тангенс угла наклона) секущей 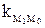может быть найден из треугольника : , тогда угловой коэффициент касательной

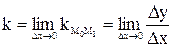
Определение. Производной функции 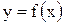называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

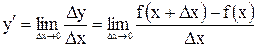
Нахождение производной функции называется дифференцированием этой функции.

Если функция в точке 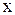имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка 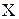, называется дифференцируемой на этом промежутке.

Из задачи о касательной вытекает геометрический смысл производной: производная 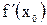есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой 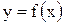в точке 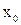, т.е. .

Тогда уравнение касательной к кривой 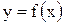в точке 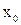примет вид

.

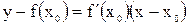2. СХЕМА ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ.

Производная функции 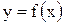может быть найдена по следующей схеме:

1. Дадим аргументу 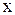приращение 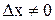и найдем наращенное значение функции .

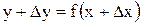2. Находим приращение функции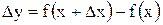

3. Составляем отношение .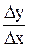

4. Находим предел этого отношения при 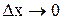, т.е. (если этот предел существует).

Пример 7.1. Найти производную функции .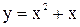

РЕШЕНИЕ.

1. Дадим аргументу 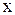приращение 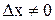и найдем наращенное значение функции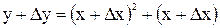

2. Находим приращение функции

.

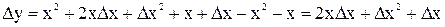3. Составляем соотношение .

4. Находим предел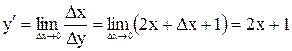

Можно доказать что для любого (не только натурального) 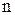справедлива формула:

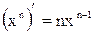
Пример 7.2. Найти производную функции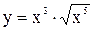

РЕШЕНИЕ.

Представим функцию в виде 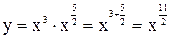, тогда по формуле 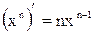найдем производную:

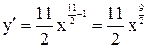
Пример 7.3. Найти уравнение касательной к кривой 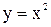в точке .

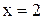РЕШЕНИЕ.

В соответствии задачи о касательной, рассмотренной выше, уравнение касательной к кривой 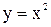в точке 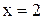имеет вид:

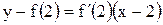
По формуле 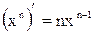найдем производную .

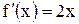Значение производной в точ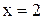ке равно . А значение функции в этой точке равно .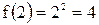

Таким образом, уравнение касательной будет иметь вид:

или .

3. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ.

1. Производная постоянной равна нулю, т.е.

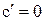
2. Производная аргумента равна 1, т.е.

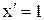
В следующих правилах будем полагать, что и 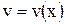- дифференцируемые функции.

3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций., т.е.

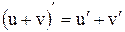
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.

СЛЕДСТВИЕ 1. Постоянный множитель можно выносить за знак производной:

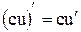
СЛЕДСТВИЕ 2. Произведение нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные. Например:

.

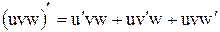5. Производная частного двух дифференцируемых функций может быть найдена по формуле

(при условии, что ).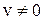

Пример 7.4. Найти производную функции 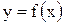и вычислить ее значение в точке .

а)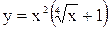

б)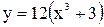

в)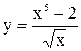

РЕШЕНИЕ. По правилам дифференцирования найдем:

а)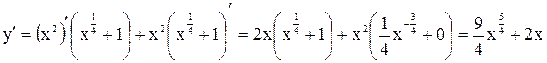

Значение производной в точке есть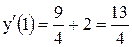

б) Сначала вынесем постоянный множитель за знак производной:

Значение производной в точке есть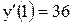

в) =

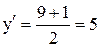
Производная функции, заданной неявно и параметрически.

Дата добавления: 2014-01-06