
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
IV. Аксиомы скалярного умножения векторов
|
|
|
|
IV1: 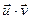 =
= 

IV2: 

IV3: 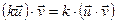
IV4: если 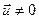 , то
, то 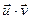 >0
>0
Если  , то
, то  :
: 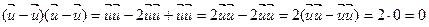
Определение 2: отображение одного евклидова векторного пространства на другое называется изоморфным, если оно:
1.) биективно;
2.) линейно;
3.) сохраняет скалярное произведение векторов;
При этом два указанных векторных пространства называются изоморфными, если одно из них можно изоморфно отобразить на другое. Vn  Vm
Vm  n = m.
n = m.
Определение 3: длиной (модулем, нормой) вектора 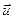 называется арифметический квадратный корень из его скалярного квадрата:
называется арифметический квадратный корень из его скалярного квадрата:
| 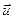 | =
| = 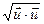 =
= 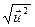 .
.
Очевидно: 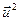 =
= 
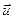

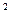 , если
, если 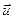 = 0, то
= 0, то 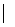
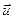
 = 0; если же
= 0; если же 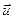 ≠ 0, то
≠ 0, то 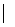
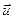
 > 0.
> 0.
Замечание 1: так как из равенства Коши – Буняковского 
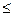
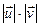 следует, что -1 ≤
следует, что -1 ≤ 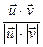 ≤ 1, то указанную дробь можно рассматривать как косинус некоторого аргумента
≤ 1, то указанную дробь можно рассматривать как косинус некоторого аргумента 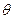 (тэта – буква греческого алфавита).
(тэта – буква греческого алфавита).
Определение 4: число 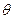 , для которого
, для которого
 =
= 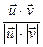 и 0 ≤
и 0 ≤ 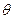 ≤
≤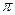 , (1)
, (1)
называется углом между векторами 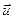 и
и 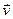 .
.
Если 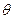 =
= 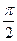 , то векторы
, то векторы 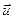 и
и 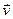 ортогональны, причем
ортогональны, причем 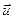
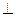
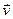

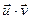 = 0.
= 0.
Если 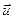 =
= 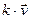 ,то
,то  и при к > 0
и при к > 0 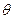 = 0, а при к < 0
= 0, а при к < 0 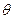 =
= 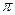 .
.
Замечание 2: из соотношения (1) следует формула скалярного произведения векторов:
 (2)
(2)
Определение 5: базис евклидова векторного пространства 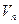 называется ортонормированным, если его векторы единичны и попарно ортогональны:
называется ортонормированным, если его векторы единичны и попарно ортогональны:
 и
и 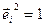 ,
, 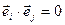 , при
, при 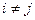 .
.
Теорема 1: в ортонормированном базисе  скалярное произведение векторов
скалярное произведение векторов 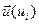 и
и 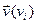 выражается формулой:
выражается формулой:
 (3)
(3)
□ 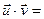 (
(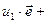 …
…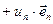 )·(
)·(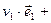 …
…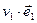 )=
)=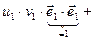
 …
…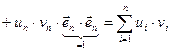 ■
■
Следствия: 1.) 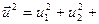 …
…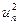 (4)
(4)
2.)  (5)
(5)
3.)  (6)
(6)
2º. Ортогональные преобразования.
Определение 6: квадратная матрица А называется ортогональной, если выполняется равенство:
 (7)
(7)
Это соотношение равносильно любому из следующих:
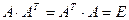 (8)
(8)
где 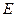 – единичная матрица,
– единичная матрица, 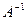 и
и 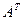 – соответственно обратная и транспонированная для
– соответственно обратная и транспонированная для 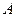 .
.
Если 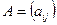 ,
,  , то из равенства (8) получаем соотношения:
, то из равенства (8) получаем соотношения:
|
|
|
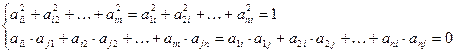 (9)
(9)
Эти равенства показывают, что при транспонировании ортогональной матрицы получается также ортогональная матрица.
Так как 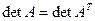 , то
, то 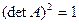 , то есть
, то есть 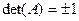 – определитель ортогональной матрицы может быть равен +1 или -1.
– определитель ортогональной матрицы может быть равен +1 или -1.
Замечание 3: формулы перехода от одного ортонормированного базиса к другому ортонормированному базису имею т ортогональную матрицу.
Определение 7: линейное преобразование 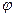 евклидова пространства
евклидова пространства 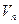 , называется ортогональным, если сохраняет длину любого вектора:
, называется ортогональным, если сохраняет длину любого вектора:  .
.
Теорема 2: ортогональное преобразование сохраняет скалярное произведение векторов.
□ Для любых векторов 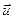 и
и 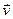 имеем:
имеем:
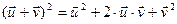 или
или 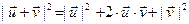 (10)
(10)
Аналогично:
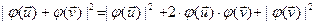 (11)
(11)
Но 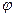 - линейное преобразование, поэтому
- линейное преобразование, поэтому 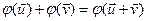 , причём из определения (7) имеем:
, причём из определения (7) имеем:
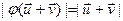 ,
,  ,
, 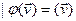 .
.
Равенство (11) перепишем в виде:
 . (12)
. (12)
Сравнивая (10) и (12), имеем требуемое:  ■
■
Следствие 1: ортогональное преобразование сохраняет углы между векторами.
Следствие 2: ортогональное преобразование переводит ортонормированный базис также в ортонормированный базис.
Замечание 4: справедливы следующие теоремы:
Теорема 3: для того чтобы линейное преобразование было ортогональным, необходимо и достаточно, чтобы его матрица относительно какого-нибудь ортонормированного базиса была ортогональной.
Теорема 4: множество ортогональных преобразований евклидова векторного пространства 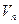 является группой.
является группой.
Определение 8: ортогональным преобразованием называется линейное преобразование, сохраняющее скалярное произведение векторов, или изоморфное отображение евклидова векторного пространства на себя.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 740; Нарушение авторских прав?; Мы поможем в написании вашей работы!