
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 4.2.3
|
|
|
|
1. m Z = { mq | q Î Z } – двусторонний идеал кольца целых чисел (Z, +, ×) для всякого целого числа m. Отметим, что для " m Î Z – m Z = m Z. Очевидно, что m Z ¹ Z, если | m | ¹ 1. Можно, например, построить следующие бесконечные цепочки двусторонних идеалов кольца Z: Z 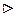 2 Z
2 Z 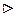 4 Z
4 Z 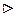 8 Z
8 Z 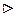 16 Z
16 Z 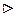 …
…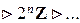 , Z
, Z 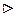 2 Z
2 Z 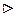 6 Z
6 Z 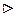 18 Z
18 Z 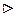 ...
...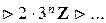 , n Î Z ³0.
, n Î Z ³0.
2. В кольце (Z / n Z, +, ×) c составным n = p × q, где 1 < p, q < n, подмножество классов вычетов 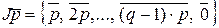 замкнуто относительно операций вычитания и умножения классов вычетов и, следовательно, образует подкольцо. Легко видеть, что
замкнуто относительно операций вычитания и умножения классов вычетов и, следовательно, образует подкольцо. Легко видеть, что 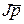 – двусторонний идеал. Аналогично, двусторонним идеалом того же кольца является множество
– двусторонний идеал. Аналогично, двусторонним идеалом того же кольца является множество 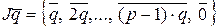 .
.
3. В матричном кольце M 2(C) (пункт 4 примера 4.2.1) подкольца J 1 и J 2 – правые, но не левые идеалы, а J 3 и J 4 – левые, но не правые идеалы. ·
Определение 4.2.5. Для каждого элемента a кольца (K, +, ×) множество aK = { a × k | k Î K } есть левый идеал кольца K, называемый главным левым идеалом, порожденным элементом a. Аналогично определяется главный правый идеал, порожденный элементом а, Ka. Двусторонний главный идеал, порожденный элементом а, является одновременно левым и правым, то есть aK = Ka, он обозначается < a >.
Определение 4.2.6. Кольцо, в котором каждый идеал является главным, называется кольцом главных идеалов.
В собственных идеалах не может быть обратимых элементов колец, так как иначе 1 Î J, тогда J = K, что приводит к противоречию. Поскольку в поле все элементы, кроме 0, обратимы, то в поле нет собственных идеалов. С другой стороны, необратимые элементы кольца, в том числе и делители нуля, порождают главные собственные идеалы. Отсюда, в частности, также следует, что в поле нет делителей нуля.
Теорема 4.2.1. (Z, +, ×) – кольцо главных идеалов.
 В (Z, +, ×), как в коммутативном кольце, все идеалы являются двусторонними.
В (Z, +, ×), как в коммутативном кольце, все идеалы являются двусторонними.
|
|
|
1. J = {0} – главный идеал. Действительно, {0} = < 0 > = {0 × k | k Î Z }.
2. Пусть теперь идеал J ¹ {0}. Докажем, что если t – наименьшее натуральное число из J, то < t > = J.
Так как t Î J, то < t > = { k × t | k Î Z } Í J. Пусть m Î J, согласно теореме 1.1.1 справедливо представление m = q × t + r, где q, r Î Z, 0 £ r < t. Тогда m – q × t = r, и если r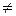 0, то в J содержится натуральное число r, меньшее t, что невозможно. Итак, m = q × t, таким образом, m Î < t >, следовательно, J Í < t >. Поэтому, J = < t >.
0, то в J содержится натуральное число r, меньшее t, что невозможно. Итак, m = q × t, таким образом, m Î < t >, следовательно, J Í < t >. Поэтому, J = < t >. 
Замечание. Согласно теореме 4.2.1 все идеалы J кольца (Z, +, ×) имеют вид < t >, где t = 0 или t – наименьшее натуральное число из J. Поскольку < t > = t Z = – t Z = < – t >, как уже отмечалось в пункте 1 примера 4.2.3, в дальнейшем можно ограничиться рассмотрением идеалов кольца (Z, +, ×) вида < t >, где t Î Z ³0.
Определение 4.2.7. Собственный идеал кольца называется максимальным, если он не содержится ни в каком другом собственном идеале данного кольца.
Рассмотрим вопрос о максимальности идеалов в кольце (Z, +, ×), которое согласно теореме 4.2.1 является кольцом главных идеалов. Очевидно, что идеал < m > является собственным в (Z, +, ×) Û m > 1.
Теорема 4.2.2. Идеал < m > максимален в (Z, +, ×) тогда и только тогда, когда m – простое число.
 Необходимость. Пусть < m > – максимальный идеал в (Z, +, ×). Если m – составное число, то m = n × q, где 1 < n, q < m, и m Î < n >, но n Ï < m >, поскольку m
Необходимость. Пусть < m > – максимальный идеал в (Z, +, ×). Если m – составное число, то m = n × q, где 1 < n, q < m, и m Î < n >, но n Ï < m >, поскольку m 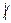 n. Следовательно, < m > Ì < n > ¹ Z, что противоречит максимальности идеала < m >. Поэтому, m – простое число.
n. Следовательно, < m > Ì < n > ¹ Z, что противоречит максимальности идеала < m >. Поэтому, m – простое число.
Достаточность. Пусть m – простое число. Рассмотрим идеал < m > в (Z, +, ×). Если < m > – не максимальный идеал, то $ n Î N >1 такое, что < m > Ì < n > ¹ Z. Тогда m = n × q для некоторого q Î N >1, что противоречит тому, что число m простое. Значит, < m > – максимальный идеал в (Z, +, ×).
|
|
|
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 344; Нарушение авторских прав?; Мы поможем в написании вашей работы!