
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство
|
|
|
|
1. Рассмотрим ряд  (15.1.4)
(15.1.4)
Так как этот ряд сходится, то выполняется необходимый признак сходимости, т.е. 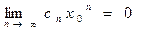 . Отсюда (в соответствии со свойствами пределов) следует, что последовательность
. Отсюда (в соответствии со свойствами пределов) следует, что последовательность  ограниченная, т.е. существует такое положительное число M, что для всех n выполняется
ограниченная, т.е. существует такое положительное число M, что для всех n выполняется
условие  . (15.1.5)
. (15.1.5)
Преобразуем ряд (15.1.4) к следующему виду: 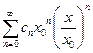
Составим ряд из абсолютных величин членов этого ряда. Получим ряд:
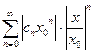 (15.1.6)
(15.1.6)
Сравним этот ряд с рядом  , который является геометрическим рядом со знаменателем
, который является геометрическим рядом со знаменателем 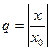 , который сходится, если
, который сходится, если  , т.е.
, т.е. 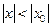 .
.
По признаку сравнения (т. 14.1.6) на основании неравенства (15.1.5) следует, что ряд (15.1.6) сходится. Следовательно, сходится, причем абсолютно, ряд (15.1.4) (т. 14.1.13).
2. Пусть ряд расходится при x = x 1. Покажем, что он расходится при любом значении | x | > | x 1|. Предположим противное: ряд сходится при некотором значении x 2, таком, что | x 2| > | x 1|. Но тогда, в соответствии с п.1 ряд должен сходиться и при x 1, что противоречит условию. Таким образом, для всех значений x, удовлетворяющих условию | x | > x 1, ряд расходится.
Геометрически это означает (рис. 15.1):
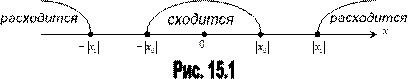 Если степенной ряд сходится в некоторой точке x 0, то он сходится в любой точке, которая ближе к точке x = 0; если степенной ряд расходится в некоторой точке x 1, то расходится в любой точке, более удаленной от точки x =0.
Если степенной ряд сходится в некоторой точке x 0, то он сходится в любой точке, которая ближе к точке x = 0; если степенной ряд расходится в некоторой точке x 1, то расходится в любой точке, более удаленной от точки x =0.
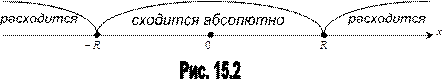
Кроме того, очевидно, что существует некоторое число R ≥ 0, такое, что при | x | < R, степенной ряд сходится, причем абсолютно, а при | x | > R ряд расходится. Это число R называется радиусом сходимости, а интервал (- R,R) – интервалом сходимости степенного ряда.
Найдем радиус сходимости. Рассмотрим ряд, составленный из абсолютных величин степенного ряда (15.1.3). При этом будем полагать, что коэффициенты этого ряда cn ≠0 при любом n. По признаку Даламбера следует: ряд сходится, если  .
.
|
|
|
Найдем 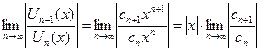
Сходимость ряда, составленного из абсолютных величин членов ряда (15.1.3) обеспечивается условием  , откуда
, откуда 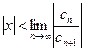 .
.
Если этот предел существует, то он и является радиусом сходимости ряда, составленного из абсолютных величин, т.е.
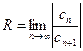 (15.1.7)
(15.1.7)
Но в таком случае сходится и сам ряд (15.1.3), причем абсолютно.
Замечание. На концах интервала сходимости, т.е.  , очевидно, применение признака Даламбера (или признака Коши) не имеет смысла, так как в этом случае
, очевидно, применение признака Даламбера (или признака Коши) не имеет смысла, так как в этом случае  , что оставляет вопрос о сходимости степенного ряда нерешенным. Для решения вопроса о сходимости степенного ряда на концах интервала сходимости следует провести дополнительное исследование числовых рядов, подставив в степенной ряд значения
, что оставляет вопрос о сходимости степенного ряда нерешенным. Для решения вопроса о сходимости степенного ряда на концах интервала сходимости следует провести дополнительное исследование числовых рядов, подставив в степенной ряд значения  .
.
Примеры. Найти радиус и интервал сходимости рядов.
1. 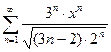 Выпишем коэффициенты ряда:
Выпишем коэффициенты ряда:


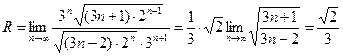 .
.
Исследуем поведение ряда на концах интервала сходимости.
Пусть 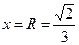 , тогда получаем ряд
, тогда получаем ряд  .
.
 Сравним этот ряд с обобщенным гармоническим рядом
Сравним этот ряд с обобщенным гармоническим рядом 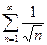 , который расходится, так как
, который расходится, так как 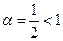 . Находим
. Находим 
 .
.
Существует конечный предел отношения общих членов рядов, значит, оба ряда ведут себя одинаково – расходятся.
Пусть 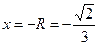 , тогда ряд имеет вид
, тогда ряд имеет вид
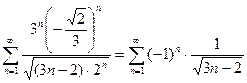 – это знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. Следовательно, он сходится. Итак, ряд сходится, если
– это знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. Следовательно, он сходится. Итак, ряд сходится, если  .
.
2.  ,
, 
Ряд сходится на всей числовой оси: -∞< x <∞
3. 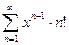 ,
, 
Ряд сходится только при x =0.
Свойства степенных рядов (без доказательств)
1. На любом отрезке [ a,b ], целиком лежащем внутри интервала сходимости (-R,R), сумма степенного ряда S(x) есть функция непрерывная.
2. Если степенной ряд c0 + c1x + c2x2 +…+ cnxn +… сходится в интервале (-R,R) к сумме S(x), то ряд, полученный почленным интегрированием данного ряда, на отрезке [ a,b ], целиком принадлежащем интервалу сходимости  также сходится, причем абсолютно, и его сумма
также сходится, причем абсолютно, и его сумма  , иными словами степенной ряд можно почленно интегрировать (как обычные суммы), т.е. если
, иными словами степенной ряд можно почленно интегрировать (как обычные суммы), т.е. если 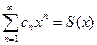 , то
, то  .
.
|
|
|
3. Если степенной ряд сходится в интервале (- R,R) к сумме S(x), то ряд, полученный почленным дифференцированием, также сходится, причем абсолютно, и его сумма 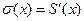 , т.е. если
, т.е. если 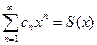 , то
, то 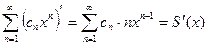
Рассмотрим степенной ряд более общего вида
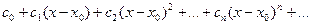 (15.1.8)
(15.1.8)
Введя новую переменную  , получаем рассмотренный ряд (15.1.4). Для него радиус сходимости вычисляется по формуле (15.1.7), т.е. ряд сходится, если
, получаем рассмотренный ряд (15.1.4). Для него радиус сходимости вычисляется по формуле (15.1.7), т.е. ряд сходится, если  , или
, или 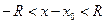 . Следовательно ряд (15.1.8) сходится, причем абсолютно, внутри интервала
. Следовательно ряд (15.1.8) сходится, причем абсолютно, внутри интервала 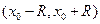 .
.
15.2 Ряды Маклорена (Тейлора)
Предположим, непрерывная и бесчисленное множество раз дифференцируемая в окрестности точки x=x 0, функция f(x) является суммой степенного ряда, т.е. тогда на основании свойства 3 степенных рядов следует
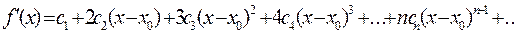
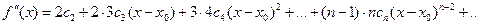
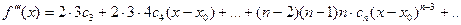
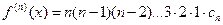
Пусть x=x 0. Из (15.1.8) и полученных производных следует
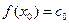

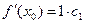
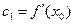
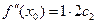
 (15.2.1)
(15.2.1)
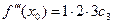

……………………………………………

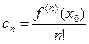
……………………………………………
Подставляя найденные значения коэффициентов в (15.1.8), получаем ряд для функции f(x).
 ,
,
который называется рядом Тэйлора.
Если x 0=0, то ряд Тейлора примет вид
 (15.2.2)
(15.2.2)
и называется рядом Маклорена для функции f(x).
Следует отметить, что не всякая функция f(x) может быть суммой ряда Маклорена. Т.е. формально для многих функций можно записать ряд Маклорена (Тэйлора). Но не всегда этот ряд будет иметь суммой функцию f(x) (сходиться к функции f(x)).
Так же, как и для числовых рядов (п.14.1) сумму f(x) ряда Маклорена можно представить в виде
 (15.2.3.)
(15.2.3.)
где Sn(x) – частичная сумма; rn(x) – n -й остаток ряда. На основании теоремы 14.4 можно сформулировать теорему.
Теорема 15.2. Чтобы ряд Маклорена сходился к функции f(x), необходимо и достаточно чтобы 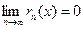 (15.2.4) (15.2.4)
|
| для всех значений x, принадлежащих интервалу сходимости. |
Можно доказать, что если функция f(x) разложима в ряд Тэйлора, то это разложение единственное.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 373; Нарушение авторских прав?; Мы поможем в написании вашей работы!