Важнейший случай СЛАУ

Алгоритмы решения СЛАУ.

1) Исследование на совместность.

2) Находим решение

В случае совпадения двух, фиксируем ранговый минор, то есть минор наивысшего порядка = k. Какой-то один (их несколько).

3) Как только выбран ранговый (базисный) минор, нужно разбить неизвестные на две группы

1 группа – основные неизвестные, т.е. из коэффициентов при которых состовляем ранговый минор. Неизвестные с теми номерами, которые имеют столбцы, в которых стоит ранговый минор.

2 группа – свободные неизвестные.Т.е. все остальные(n-r).

4) Все уравнения, коэффициенты из которых не входят в ранговый минор – вычеркиваются, остаются только r-уравнений. Потому что все остальные строки – решение линейно-ранговой подсистемы. Все члены со свободными неизвестными переносятся в правые части. Получается новая подсистема с числом неизвестных r. Имеется новая СЛАУ – квадратная относительно основных неизвестных. Но в правой части комбинация с коэффициентами неизвестных. Свободным неизвестным придаем мысленно какие-либо значения, фиксируем, т.е. получаем полную новую систему, но их бесконечное множество. Система получается крамеровской. Определитель ≠0⇒всякая такая система, получающаяся фиксацией, будет иметь одинаковые решения, которые можно найти по формуле Крамера. Но т.к. свободных членов >0(0,когда n=r), то сводится к виду трапеции.

Однородные СЛАУ – называется однородной, если все её свободные члены нули(столбцов свободных членов 0).

- приведенная однородная система

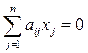
1≤ i ≤ m

- в вещественном виде

- в комплексном виде

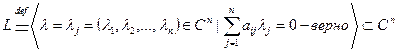
L– множество решений однородной СЛАУ(1).

Теорема о Lподпространство в Rⁿ

Сумма любых двух решений вновь решение.

λ=(λ_j) и β=(β_j)∊L

γ=λ+β=(γ_j=λ_j+β_j)⇒

Система совместна всегда, так как есть всегда 0 решений.

Теорема о базисе и размерности пространства решений однородной СЛАУ.

Пусть задана произвольная однородная СЛАУ(1).

1) r=rangA=rang(α_ij) (r≤m)

2) фиксируем ранговый минор, не ограничивая общности.

3) Разбиваем на 2 группы

x₁, x₂,…, x_r- основные

x_r+1, x_r+2,…, x_n- свободные

1≤i≤r, n≤m

	xr+1	xr+2	.	.	xn
λ1	λ1,r+1	λ1,r+2	.	.	λ1,n
λ2	λ2,r+1	λ2,r+2	.	.	λ2,n
.	.	.	.	.	.
.	.	.	.	.	.
λn-r	λn-r,r+1	λn-r,r+2	.	.	λn-r,n

n-r – серия свободных неизвестных, определитель должен быть отличен от нуля.

λ ₁=(λ_1,1,…, λ_1,r, λ_1,r+1,…, λ_1,n)∊L

λ ₂=(λ_2,1,…, λ_2,r, λ_2,r+1,…, λ_2,n)∊L

…………………………………

λ _n-r=(λ_n-r,1,…, λ_n-r,r, λ_n-r,r+1,…, λ_n-r,n)∊L

Пусть β – произвольные решения

β =(β₁,…, β_r, β_r+1,…, β_n), где (β₁,…, β_r) – основные, (β_r+1,…, β_n) – свободные.

Пример:

dimL₁

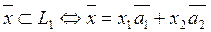
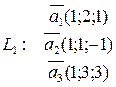
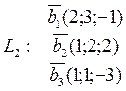
rangL₁=2

rangL₂=2

Связь решений произвольной СЛАУ и её приведенной однородной.

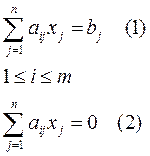
Теорема 1. Разность любых двух решений СЛАУ(1) будет решением её приведенной системы.

Теорема 2. Сумма любого частного решения системы(1) и любого решения системы(2) является частным решением системы(1).

Теорема 3. Сумма любого частного решения системы(1) и общего решения его приведенной системы(2) является общим решением системы(1).

Дата добавления: 2014-01-07