Математическое ожидание

СЛУЧАЙНЫХ ВЕЛИЧИН

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ

Решение.

.

.

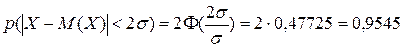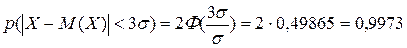Задача 103. Непрерывная случайная величина X распределена по нормальному закону с параметрами 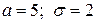. Найти вероятность того, что в результате испытания X попадет в интервал (-1; 6).

Решение.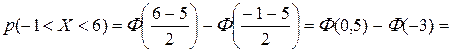

= 0,1915-(-0,4987)=0,6902.

Часто совсем необязательно знать о случайной величине все. Например, владельца облигаций вряд ли будет интересовать полная картина распределения вероятностей выигрышей. Но он наверняка хотел бы знать, на какой средний годовой доход он может рассчитывать, а также каковы наиболее вероятные вариации этого дохода.

Можно выделить несколько числовых характеристик, которые многое могут сказать о свойствах данной случайной величины. Самая первая, наиболее часто используемая характеристика, называется математическим ожиданием, или средним значением. Формула, определяющая математическое ожидание, подобна формуле, по которой вычисляют среднее из нескольких чисел.

Если среди n чисел n ₁ равны числу x ₁, n ₂ равны числу x ₂, …, n_m чисел равны числу x_m (n ₁ + n ₂ + … + n_m = n), то их среднее арифметическое вычисляется по формуле

При этом 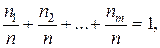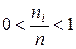, i = 1, 2, …, m, так что отношения (частоты) 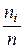по своим свойствам напоминают вероятности.

Пусть Х – дискретная случайная величина, имеющая закон распределения { x_i, p_i }.

Математическим ожиданием, или средним значением, случайной величины X называют число M (X), определяемое формулой

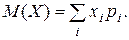(9.1)

Когда величина X принимает бесконечное число значений, требуется, чтобы написанный ряд сходился абсолютно. Тогда говорят, что X имеет конечное математическое ожидание. Если ряд 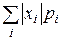расходится, говорят, что дискретная случайная величина X не имеет конечного математического ожидания.

Пример 1. (Из недавнего прошлого). Найти среднее значение выигрыша на одну карточку спортлото «5 из 36». Карточка стоит 30 коп. Угадавший 5 номеров получает 10 000 руб., угадавший 4 номера получает 50 руб., угадавший 3 номера получает 5 руб.

Случайная величина Х – чистый выигрыш игрока, купившего 30- копеечную карточку, принимает четыре разных значения: 9999,7, 49,7, 4,7 и –0,3 руб. Рассчитаем вероятности этих значений.

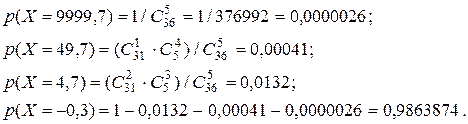
Найдем математическое ожидание М (Х) выигрыша на одну карточку.

М (Х) = 9999,7·0,0000026 + 49,7·0,00041+ 4,7·0,0132 – 0,3·0,9863874 =

= -0,1875. Средняя потеря игрока в одной игре равна примерно 19 коп.

Пример 2. Найти математическое ожидание случайной величины, имеющей распределение Пуассона.

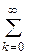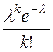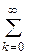Нужно просуммировать ряд k .

k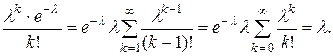

В соответствии с определением функции дискретной случайной величины получаем, что математическое ожидание функции φ (X) равно

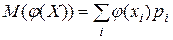. (9.2)

Если значений x_i бесконечно много, то для существования математического ожидания ряд в правой части должен сходиться абсолютно.

Пример 3. Случайная величина Х задана законом распределения:

xi	-2	-1
pi	0,3	0,1	0,1	0,4	0,1

Найти математическое ожидание случайной величины Х ². Составим сначала закон распределения случайной величины Х ²:

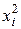
pi	0,1	0,5	0,4

Тогда М (Х ²) = 0·0,1 + 1·0,5 + 4·0,4 = 2,1.

Пример 4. Математическое ожидание линейной функции случайной величины X, 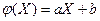, где a и b – данные числа, равно

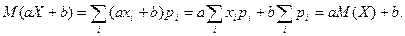
Предполагалось, что число М (X) существует. В частности, М (аХ) =

= аМ (Х), М (b) = b.

Пример 5. Задано совместное распределение случайных величин Х и Y. Найти М (Х), М (Y), М (Х + Y).

yj xi	-1
	0,05	0,1	0,05	0,1
	0,05	0,05	0,05	0,1
	0,2	0,01	0,14	0,1

Составим законы распределения случайных величин Х и Y. Случайная величина Х принимает значение 0 с вероятностью 0,05 + 0,1 + 0,05 + 0,1 = = 0,3; значение 1 с вероятностью 0,05 + 0,05 + 0,05 + 0,1 = 0,25; значение 2 с вероятностью 0,2 + 0,01 + 0,14 + 0,1 =0,45.

Случайная величина Y принимает значение –1 с вероятностью 0,05 + 0,05 + 0,2 = 0,3; значение 2 с вероятностью 0,1 + 0,05 + 0,01 = 0,16; значение 3 с вероятностью 0,05 + 0,05 + 0,14 = 0,24; значение 4 с вероятностью 0,1 + 0,1 + 0,1 = 0,3.

Законы распределения Х и Y:

xi					yj	-1
pi	0,3	0,25	0,45	qi	0,3	0,16	0,24	0,3

Отсюда М (Х) = 0·0,3 + 1·0,25 + 2·0,45 = 1,15; М (Y) = -1·0,3 + 2·0,16 +

+ 3·0,24 + 4·0,3 = 1,94.

Составим закон распределения суммы Х + Y.

Х + Y	-1
pi	0,05	0,05	0,2	0,1	0,1	0,16	0,24	0,1

М (Х + Y) = -1·0,05 + 0·0,05 + 1·0,2 + 2·0,1 + 3·0,1 + 4·0,16 + 5·0,24 + 6·0,1 = 3,09 = М (Х) + М (Y).

Последнее совпадение не случайно, справедлива теорема:

Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, если последние существуют.

Это утверждение переносится на любое конечное число слагаемых. Докажем его.

Итак, пусть М (Х) и М (Y) существуют. Тогда

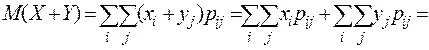
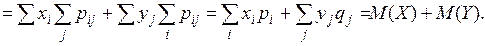
Правомерность действий вытекает из условия абсолютной сходимости рядов.

Пример 6. Найти математическое ожидание произведения случайных величин Х и Y из примера 5.

Закон распределения произведения ХY таков (табл. 9.1)

Таблица 9.1

xy	-2	-1
pij	0,2	0,05	0,3	0,05	0,05	0,11	0,14	0,1

Следовательно, М (ХY) = -2·0,2 + -1·0,05 + 0·0,3 + 2·0,05 + 3·0,05 + 4·0,11 + 6·0,14 + 8·0,1 = 1,88.

В общем случае математическое ожидание произведения случайных величин не равно произведению их математических ожиданий. Но если случайные величины Х и Y независимы, иначе говоря, p_ij = p_iq_j, то верна теорема:

Дата добавления: 2014-01-07