
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условие ортогональности двух векторов
|
|
|
|
Скалярным произведением двух векторов называем число, равное произведению длин этих векторов на косинус угла между ними.
Обозначать операцию скалярного произведения векторов 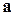 и
и 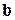 будем символом
будем символом 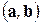 . По определению,
. По определению,
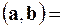
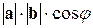 . (1.13)
. (1.13)
Например, для ортов 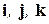 по определению имеем:
по определению имеем:
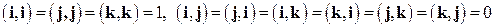 .
.
Действительно, длина каждого из ортов  равна единице, а угол между каждой парой равен или
равна единице, а угол между каждой парой равен или 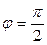 , тогда
, тогда 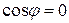 , или
, или 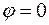 , тогда
, тогда 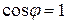 .
.
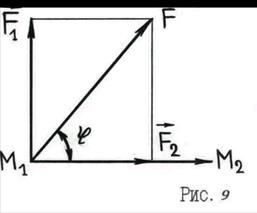 Понятие скалярного произведения возникло в механике в связи с вычислением работы
Понятие скалярного произведения возникло в механике в связи с вычислением работы  , которая выполняется силой
, которая выполняется силой  при перемещении материальной точки из положения
при перемещении материальной точки из положения  в положение
в положение  . Пусть сила
. Пусть сила  образует угол
образует угол 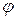 с вектором перемещения
с вектором перемещения 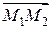 (рис.9). Разложим силу
(рис.9). Разложим силу  на составляющие:
на составляющие: 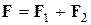 . Составляющая
. Составляющая 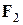 имеет с вектором
имеет с вектором 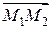 одинаковое направление, а составляющая
одинаковое направление, а составляющая 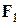 перпендикулярна к нему. Работу выполняет только составляющая
перпендикулярна к нему. Работу выполняет только составляющая 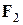 :
: 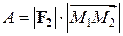 .
.
Поскольку 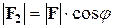 , то
, то
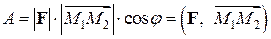 (1.14)
(1.14)
Так как 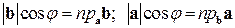 , то формуле (1.13) можно придать вид:
, то формуле (1.13) можно придать вид:
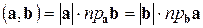 . (1.15)
. (1.15)
Геометрические свойства скалярного произведения.
1) Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
2) Два ненулевых вектора образуют острый (тупой) угол тогда и только тогда, когда их скалярное произведение есть положительное (отрицательное) число.
Алгебраические свойства скалярного произведения.
1) 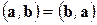
2) 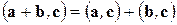
3) 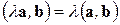
4) 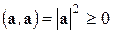 для
для 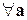 ,
, 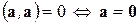
Алгебраические свойства позволяют при скалярном умножении линейных комбинаций векторов раскрывать скобки, как при обычном умножении. Коммутативность скалярного произведения (свойство 1) позволяет не следить за порядком множителей.
Задача 1. Вычислить скалярное произведение векторов 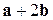 и
и 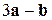 , если
, если  , а угол между векторами
, а угол между векторами 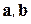 равен
равен 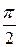 .
.
Решение. Используя алгебраические свойства скалярного произведения, запишем:
|
|
|
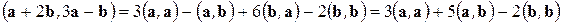 .
.
По условию, векторы 
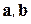 ортогональны, значит,
ортогональны, значит,  . Окончательно получаем
. Окончательно получаем
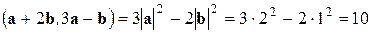 .¨
.¨
Если векторы 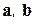 определены своими декартовыми координатами
определены своими декартовыми координатами
 ,
,
то скалярное произведение этих векторов равно сумме произведений соответствующих координат, то есть
 . (1.16)
. (1.16)
Это следует из определения и свойств скалярного произведения.
Задача 2. Докажите формулу (1.16). ♦
Указание. Записать разложение векторов 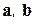 по базису
по базису 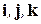 , затем воспользоваться алгебраическими свойствами скалярного произведения.¨
, затем воспользоваться алгебраическими свойствами скалярного произведения.¨
Угол 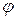 между векторами
между векторами 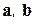 определяется формулой
определяется формулой
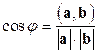 или
или 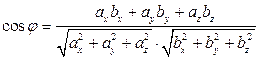 . (1.17)
. (1.17)
Из формулы (1.17) следует, что условие ортогональности двух векторов в координатной форме имеет вид:
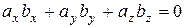 . (1.18)
. (1.18)
Задача 3. Даны векторы 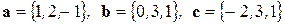 . Найти скалярное произведение
. Найти скалярное произведение 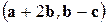 .
.
Решение. Задачу можно решить двумя способами.
1. Найдем координаты векторов 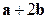 и
и 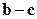 :
: 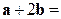
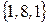 ,
, 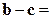
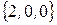 .
.
Скалярное произведение этих векторов найдем по формуле (1.16):
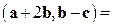
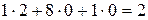 .
.
2. Вспомним алгебраические свойства скалярного произведения:
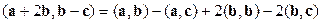 .
.
Найдем 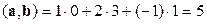 ,
,
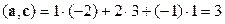 ,
,
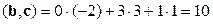 ,
,
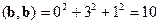 .
.
Значит, 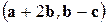 =
= 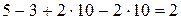 .¨
.¨
Задача 4. Даны векторы  . Найти
. Найти
1) 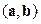 , 2)
, 2) 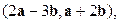 3)
3) 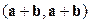 , 4)
, 4) 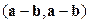 .
.
Ответ. 1) 22, 2) –200, 3) 129, 4)41.¨
Задача 5. Найти вектор 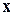 , если известно, что он коллинеарен с вектором
, если известно, что он коллинеарен с вектором 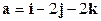 , имеет длину
, имеет длину 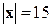 и образует с ортом
и образует с ортом  острый угол.
острый угол.
Решение. По условию, векторы 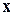 и
и 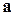 коллинеарны, значит, пропорциональны:
коллинеарны, значит, пропорциональны: 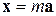 . Поэтому координаты вектора
. Поэтому координаты вектора 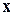 в
в 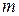 раз больше соответствующих координат вектора
раз больше соответствующих координат вектора 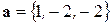 :
: 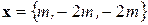 . По формуле (1.3) запишем длину вектора
. По формуле (1.3) запишем длину вектора 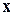 :
:
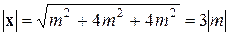 =15
=15 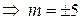 .
.
Знак коэффициента т выясним, опираясь на геометрические свойства скалярного произведения. По условию, угол между вектором 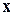 и ортом
и ортом 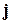 острый, т.е. скалярное произведение
острый, т.е. скалярное произведение 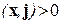 . Так как
. Так как 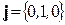 , то
, то
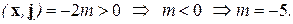
Окончательно 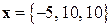 .¨
.¨
Задача 6. Вычислить работу силы 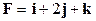 при перемещении материальной точки из положения
при перемещении материальной точки из положения 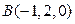 в положение
в положение 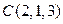 .
.
Решение. Сначала вычислим координаты вектора  :
: 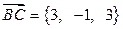 . Работу силы
. Работу силы 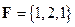 при перемещении материальной точки из начала вектора
при перемещении материальной точки из начала вектора  в его конец вычислим по формуле (1.14):
в его конец вычислим по формуле (1.14): 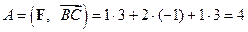 . ¨
. ¨
Задача 7. Вычислить работу, выполняемую силой 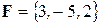 , когда точка ее приложения перемещается из начала вектора
, когда точка ее приложения перемещается из начала вектора 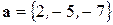 в его конец.
в его конец.
|
|
|
Ответ. 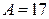 . ¨
. ¨
Задача 8. При каком значении числа 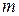 векторы
векторы 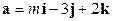 и
и 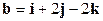 взаимно перпендикулярны?
взаимно перпендикулярны?
Решение. Условие ортогональности (1.18) для векторов 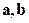 принимает вид
принимает вид 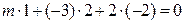 , откуда находим
, откуда находим 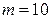 . ¨
. ¨
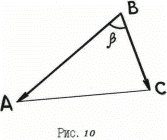
Задача 9. Даны вершины треугольника 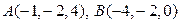 и
и 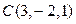 . Найти его внутренний угол при вершине
. Найти его внутренний угол при вершине 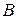 (рис. 10).
(рис. 10).
Решение. Найдем координаты векторов 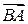 и
и  :
:
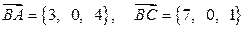 .
. 
Косинус угла 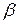 при вершине
при вершине 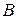 найдем по формуле (1.17):
найдем по формуле (1.17):
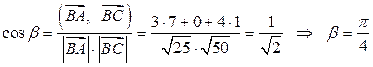 . ¨
. ¨
Задача 10. Заданы векторы 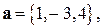

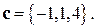 Найти
Найти 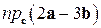 .
.
Решение. Вычислим сначала вектор 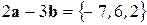 , потом скалярное произведение
, потом скалярное произведение 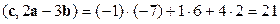 , наконец, найдем длину вектора
, наконец, найдем длину вектора 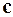 :
: 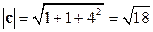 . Теперь, в соответствии с формулой (1.15) запишем
. Теперь, в соответствии с формулой (1.15) запишем 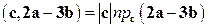 , откуда находим
, откуда находим 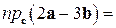
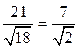 . ¨
. ¨
Если один из множителей – единичный вектор, то скалярное произведение в соответствии с (1.15) равно проекции второго множителя на направление первого. Значит, координаты  произвольного вектора
произвольного вектора 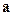 в декартовом базисе
в декартовом базисе 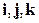 , определенные формулами (1.5), можно найти как скалярные произведения
, определенные формулами (1.5), можно найти как скалярные произведения
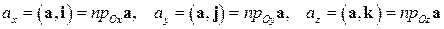
Задача 11. Вектор 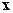 перпендикулярен векторам
перпендикулярен векторам 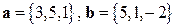 и удовлетворяет условию
и удовлетворяет условию 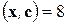 , где вектор
, где вектор 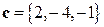 . Найти этот вектор.
. Найти этот вектор.
Решение. Пусть 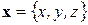 . Для нахождения трех неизвестных координат
. Для нахождения трех неизвестных координат 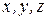 имеем систему линейных уравнений:
имеем систему линейных уравнений:
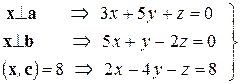
Вычислим определители (см. раздел 1.6):
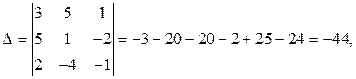
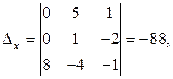
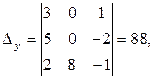
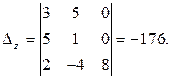
Теперь по формулам Крамера найдем
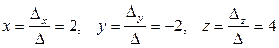
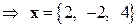 . ¨
. ¨
Задача 12. Найти вектор 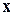 , если известно, что он перпендикулярен к векторам
, если известно, что он перпендикулярен к векторам 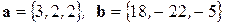 , имеет длину
, имеет длину 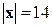 и образует с осью
и образует с осью 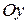 тупой угол.
тупой угол.
Решение. Пусть 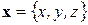 . По условию
. По условию
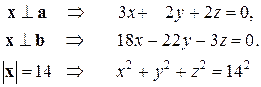
Выразим из первых двух уравнений 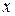 и
и 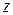 через
через 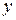 :
: 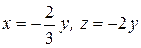 . Воспользуемся условием
. Воспользуемся условием 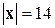 :
: 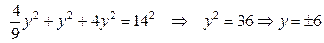 .
.
Из двух знаков надо выбрать "минус", так как по условию угол между искомым вектором 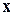 и вектором
и вектором 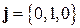 тупой, то есть
тупой, то есть 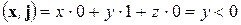 . Значит,
. Значит, 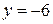 , тогда
, тогда 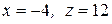 , а вектор
, а вектор 
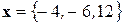 . ¨
. ¨
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 2549; Нарушение авторских прав?; Мы поможем в написании вашей работы!