Исследование на экстремум

Приложение производной к исследованию функций.

Исследование на монотонность

Определение. Если знаки приращений функции и аргумента в данной точке совпадают, то функцию называют возрастающей в данной точке.

В противном случае функцию называют убывающей в данной точке.

Из этих определений следует теорема: если производная функции в данной точке положительна, то функция в этой точке возрастает (если производная отрицательна, то функция убывает).

Доказательство. Из определения производной 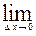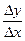следует утверждение этой теоремы.

Получаем алгоритм исследования функции y=f(x) на монотонность.

1-й шаг. Найди область определения функции.

2-й шаг. Найди производную f’(x) функции.

3-й шаг. Найди точки, в которых f’(x) равна нулю, и точки, в которых f’(x) не существует.

4-й шаг. Точками, найденными на шаге 3, разбей область определения на промежутке.

5-й шаг. В каждом промежутке возьми точку и установи(узнай, выясни) знак производной в выбранной точке. Сделай вывод и возрастании-убывании функции.

Определение. Если в окрестности точки x_o выполняется условие f(x)<f(x_o), то эту точку называют точкой локального экстремума типа максимум.

Если в окрестности точки x_o выполняется условие f(x)>f(x_o), то эту точку называют точкой локального экстремума типа минимум.

В этих определениях слово «локальный» означает достаточно малую окрестность рассматриваемой точки.

Среди всех локальных экстремумов можно выбрать самое малое и самое большое значения, которые называют глобальными экстремумами.

Предполагается также, что функция и ее производная непрерывны в указанной точке.

Теорема (необходимое условие существования). Если f(x) дифференцируема в точке x_o и эта точка является точкой локального экстремума, то f’(x_o).

Теорема (1-е достаточное условие).Если f(x) непрерывна в x_o, дифференцируема в окрестности этой точки, кроме, быть может, самой точки и при переходе через эту точку производная меняет знак, то точка x_o – точка локального экстремума.

Переход через точку означает такое изменение аргумента, при котором в начале движения аргумент принимал значение с одной стороны точки x_o, а закончился процесс, когда аргумент принял значение с другой стороны точки x_o.

Теорема(2-е достаточное условие). Пусть f(x) непрерывна в x_o и дифференцируема в этой точке до порядка n включительно. Пусть f⁽ⁱ⁾(x)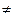0 для i=1,2,…,n-1, но f⁽ⁿ⁾(x)= 0. Тогда, если n четное, то в точке x_o есть экстремум; если n нечетное, то в точке x_o нет экстремума.

Если же n нечетно, то на знак разности f(x)-f(x_o) влияет еще и знак величины (x-x_o)ⁿ, который может быть разным для разного расположения х относительно точки x_o. Значит определения экстремума не выполняется и его нет.

Следствие. Если знак f⁽ⁿ⁾(x_о) положителен, то x_о – точка локального максимума; если знак f⁽ⁿ⁾(x_о) отрицателен, то x_о – точка локального минимума.

На практике ограничиваются второй производной.

Дата добавления: 2014-10-23