Асимптоты плоских кривых

Исследование на выпуклость графика функции.

Сначала несколько новых терминов. Предполагаем, что любая невертикальная прямая разбивает плоскость на «верхнюю» и «нижнюю» полуплоскости.

Пусть в x_o функция f(x) имеет касательную, непараллельную оси Оу. При таком условии мы предполагаем дифференцируемость функции в это й точке.

Определение. Кривая выпукла (вариант - вогнута) в точке x_o, если в достаточно малой окрестности этой точки кривая расположена ниже (вариант – выше) касательной.

Определение. Кривая выпукла (вариант - вогнута) в интервале, если она такова в каждой точке интервала.

Пусть в x_o f(x) имеет касательную (в том числе и параллельную оси Оу).

Определение. Точка x_o называется точкой перегиба кривой у= f(x), если с одной стороны от точки x_o кривая у= f(x) выпукла, а с другой – вогнута.

Теорема. Если f(x) в окрестности x₀ дважды дифференцируема, то необходимым и достаточным условием выпуклости (вариант – вогнутости) графика этой функции в точке x₀ является условие постоянства знака для f’’(x₀).

Пусть требуется доказать необходимость в теореме; тогда, если кривая выпукла в точке x₀, то все точки кривой в окрестности этой точки расположены ниже касательной и потому левая часть равенства отрицательна; но в этом случае имеем постоянный отрицательный знак для f’’(x₀) (аналогично для вогнутого графика).

Пусть требуется доказать достаточность теоремы; тогда знак производной постоянен (пусть отрицателен); поэтому правая часть формулы отрицательна и потому все точки кривой расположены ниже точек касательной.

Следствие. Если f(x) дважды дифференцируема, то в точке перегиба ее графика верно равенство f’’(x)=0. Утверждение следует из предыдущей теоремы – касательная существует и единственна, а знак непрерывной f’’(x) меняется при переходе через точку и потому в точке равен нулю (см. свойства функции, непрерывной на промежутке и следствие из них).

Из всех этих рассуждений следует алгоритм исследования функции на выпуклость-вогнутость ее графика.

1-й шаг. Укажи область определения функции.

2-й шаг. Найди 2-ю производную функции.

3-й шаг. Реши уравнение f’’(x)=0 (найди нули 2-й производной).

4-й шаг. Точками, найденными в п.3. разбей область определения на промежутки.

5-й шаг. На каждом промежутке возьми точку и установи (узнай, выясни) знак 2-й производной в этой точке. Сделай вывод.

Определение. Линия, к которой неограниченно приближается кривая, называется асимптотой этой кривой.

Специально не оговаривается как ведет себя кривая относительно асимптоты (пересекает асимптоту или нет).

Примером такого рода асимптоты будет экспонента 0,5е^х для гиперболической функции y=Shx.

Будем рассматривать только прямолинейные односторонние асимптоты, которые имеют вид y=kx+b, y=b, x=a. Начнем с простейших – вертикальных. Если в некоторой точке х=а функция y=f(x) не определена, то имеет смысл вычислить односторонние пределы этой функции в этой точке. Если хотя бы один из односторонних пределов есть бесконечный предел, то прямая х=а – вертикальная асимптота.

Пусть мы строим график функции y=f(x). И возник вопрос о наличии асимптоты вида y=kx+b. Поступаем так. По определению разность f(x)- (kx+b)=a(x) - бмв при х 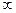или при х-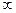. Разделим обе части равенства на х и подсчитаем пределы обеих частей при тех же условиях. Получаем

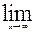
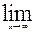
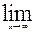
-k -= 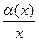Откуда получаем k=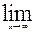 т.к. остальные пределы дают нули. Если же просто подсчитать при тех же условиях пределы 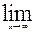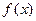-kх -b=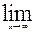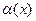, то получим b=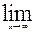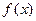-kх.

Частный случай. При k=0 получают горизонтальную асимптоту y=b.

Общая схема исследования и построение графиков.

Обобщаем все ранее приведенные исследования функции и получаем алгоритм исследования функции и построения ее графика.

1-й шаг. Найди область определения функции.

2-й шаг. Найди производную f’(x) функции.

3-й шаг. Найди точки, в которых f’(x) равна нулю, и точки, в которых f’(x) не существует.

4-й шаг. Найди 2-ю производную функции.

5-й шаг. Реши уравнение f’’(x)=0 (найди нули 2-й производной). Найди точки, где f’’(x) не существует

6-й шаг. Точками, найденными в п.п.3 и 5. разбей область определения на промежутки.

7-й шаг. В каждом промежутке возьми точку и установи(узнай, выясни) знак производной в выбранной точке. Сделай вывод о возрастании-убывании функции; наличии экстремума и вычисли значения экстремума.

8-й шаг. На каждом промежутке возьми точку и установи (узнай, выясни) знак 2-й производной в этой точке. Сделай вывод о выпуклости-вогнутости графика функции в этом промежутке, наличии точек перегиба и вычисли значения функции в точках перегиба.

Примечание. Пункты 6,7,8 лучше выполнять в сводной (результативной) таблице. 1-я строка таблицы – промежутки и точки из п.п.3 и 5. 2-я строка – знаки f’(x) по промежуткам и на границах промежутков. 3-я строка – знаки f’’(x) по промежуткам и на границах промежутков. Последняя строка отводится для символов, которые характеризуют поведение функции и ее графика: - возрастает; - убывает; - выпукла и убывает;

- выпукла и возрастает; - вогнута и возрастает; - вогнута и убывает. Все это облегчит в дальнейшем построение графика.

9-й шаг. Исследуй точки разрыва на наличие вертикальных асимптот.

10-й шаг. Найди возможные наклонные асимптоты при графика при х 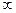или при х -.

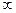11-й шаг. Выбери масштаб руководствуясь значениями экстремумов, перегибов и их координат. Изобрази асимптоты, экстремумы, перегибы.

12-й шаг. Плавной линией соедини все участки кривой, двигаясь слева направо.

Примечание. Некоторые из пунктов могут меняться местами (например, п.п.9 и 10 могут выполняться сразу за п.1.).

Контрольные вопросы и задания для самостоятельной подготовки:

1. Теорема Ферма.

2. Теорема Ролля.

3. Теорема Лагранжа.

4. Теорема Коши.

5. Раскрытие неопределённостей. Правило Лопиталя.

6. Приложение производной к исследованию функции. Интервалы монотонности.

7. Приложение производной к исследованию функции. Отыскание точек локального экстремума функции.

8. Приложение производной к исследованию функции. Направление выпуклости и точки перегиба графика функции.

9. Асимптоты графика функции.

10. Схема исследования функции. Построение графика функции.

11. Наибольшее и наименьшее значения функции на отрезке.

12. Найти точки пергибы и интервалы выпуклости функции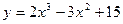

13. Найти точки пергибы и интервалы выпуклости функции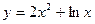

14. Найти точки пергибы и интервалы выпуклости функции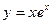

15. Найти точки пергибы и интервалы выпуклости функции

16. Найти асимптоты графика функции

17. Найти асимптоты графика функции

18. Найти асимптоты графика функции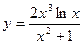

19. Исследовать функцию и построить график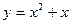

20. Исследовать функцию и построить график

Дата добавления: 2014-10-23